第一章 随机事件及其概率 教学基本要求: 1、了解随机事件的定义,理解样本空间的定义,明白事件之间的关系同运算。 2、明白事件概率的定义。 3、了解概率的古典概念,会计算简单的古典概率。 4、了解概率的基本性质与加法法则。 5、了解条件概率的概念,明白概率的乘法公式、全概率公式同贝叶斯公式。 6、了解事件独立性的定义,会计算相互独立事件的相关概率。 重点: 随机事件及其关系 古典概率 概率性质 条件概率与乘法公式 全概率公式与贝叶斯公式 事件的独立性
难点: 古典概率 全概率公式与贝叶斯公式
第一节 随机事件 一、随机试验 在自然界中存在各种各样的现象,其中有一类现象是在一定条件下必然出现某种结果.例如,在地球的引力作用下,上抛物体一定会落下;水在一定的温度下会变成气体等.把这类现象叫做确定现象.还有另一类现象是在一定条件下可能出现这样的结果,也可能出现那样的结果.例如,抛一枚硬币,其落下的结果可能是国徽面向上,也可能数字面向上.又如,进行一次环靶射击,其结果可能是击中0环,1环, ,10环等,把这类现象叫做随机现象.其特点是在一定条件下,出现的结果不止一个,事先不能确定哪个结果一定会出现,即呈现出不确定性. ,10环等,把这类现象叫做随机现象.其特点是在一定条件下,出现的结果不止一个,事先不能确定哪个结果一定会出现,即呈现出不确定性. 随机现象虽然呈现出结果的不确定性,但是人们经过大量重复试验或观察发现,它却具有内在的必然性,即规律性,叫做统计规律性. 人们往往通过试验来研究随机现象的统计规律.这种试验具有如下特征: 1 在相同条件下可以重复进行; 2 每次试验可能出现的结果不止一个,并且试验前可以知道所有可能出现的结果; 3 每次试验前不能确定哪一个结果一定会出现. 这种试验叫做随机试验,简称试验,记作E. 二、样本空间与随机事件 1. 样本空间 定义 把随机试验E的所有可能结果构成的集合叫做E的样本空间,记作Ω.样本空间的元素(E每个可能结果)叫做样本点,记作ω. 例1 将一枚硬币在光滑地面上抛掷两次,观察正面H、反面T出现的情况,试写出此试验的样本空间. 解 因为第一次抛掷可能出现的结果为:H、T,所以抛掷完两次后的可能结果为:HH,TH,HT,TT,故此试验的样本空间为 Ω={HH,TH,HT,TT}. 2. 随机事件 定义 随机试验E的样本空间 的子集叫做随机事件,简称为事件,用英文字母 的子集叫做随机事件,简称为事件,用英文字母 、 、 、C,及 、C,及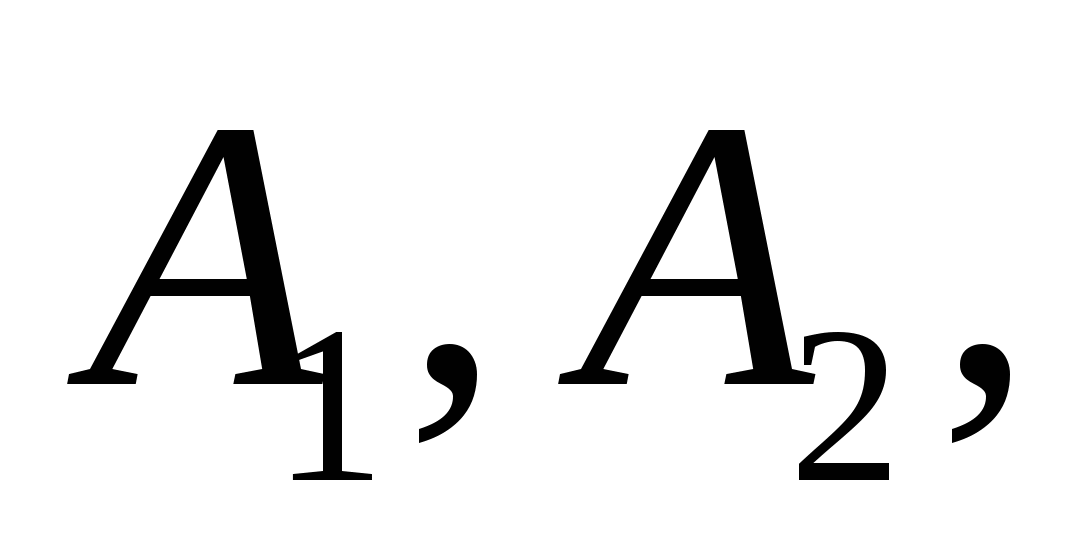 …等表示. …等表示. 因为每个样本点都是样本空间的子集,所以样本点也是随机事件,称它们为基本事件.随机事件在一次试验中,可能出现,也可能不出现.我们说某个事件出现,当且仅当它所包含的某个基本事件出现.例如在E1中,如果记 ={出现偶数点},则 ={出现偶数点},则 ={ ={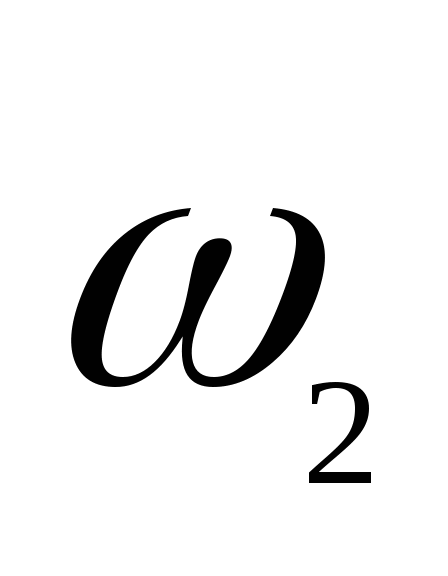 , , , ,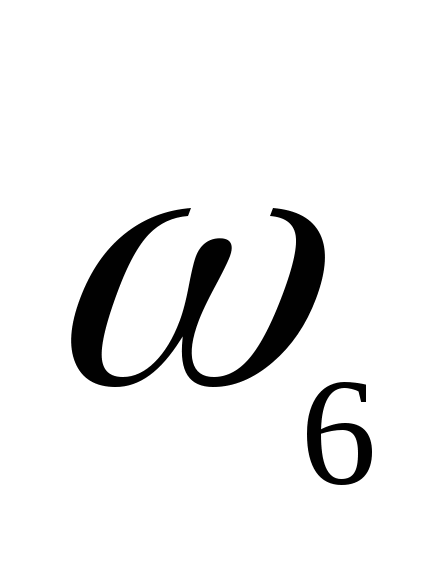 },当且仅当“2点”,“4点”和“6点”中有一个出现就说事件 },当且仅当“2点”,“4点”和“6点”中有一个出现就说事件 出现.再如, 出现.再如, ={出现点数小于3}={ ={出现点数小于3}={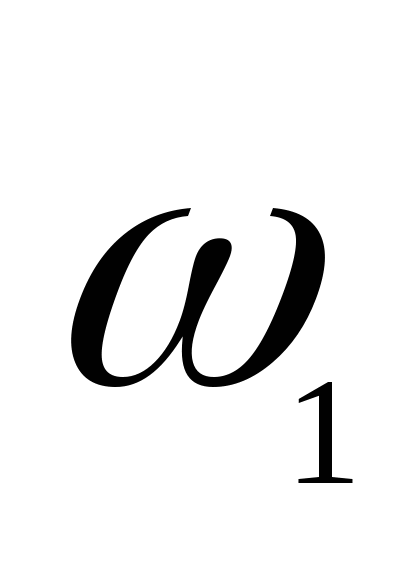 , ,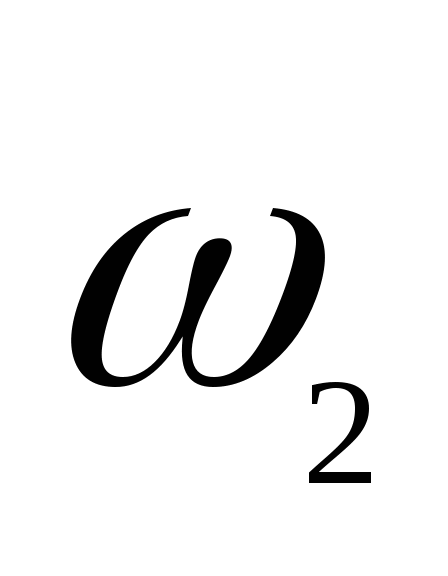 },当且仅当“1点”、“2点”中有一个出现就说事件 },当且仅当“1点”、“2点”中有一个出现就说事件 出现. 出现. 在随机试验中,由于样本空间 也是它自身的子集,所以 也是它自身的子集,所以 也是随机事件.在每一次试验中都出现的事件叫做必然事件,显然样本空间 也是随机事件.在每一次试验中都出现的事件叫做必然事件,显然样本空间 是必然事件,必然事件也记作 是必然事件,必然事件也记作 .每一次试验中都不出现的事件叫做不可能事件,记作 .每一次试验中都不出现的事件叫做不可能事件,记作 .例如,在E1中,“大于6点”的事件就是不可能事件. .例如,在E1中,“大于6点”的事件就是不可能事件. 3. 事件间的关系及其运算 设试验E的样本空间为 ,且 ,且 、 、 、 、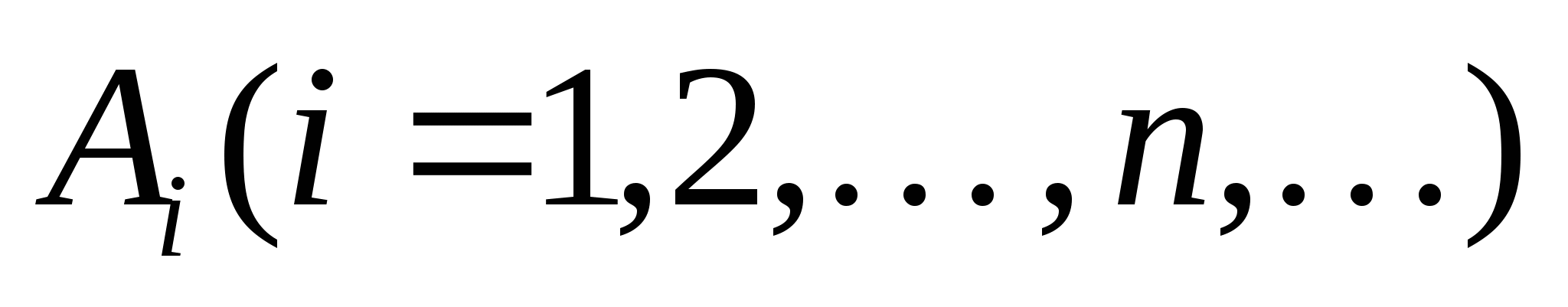 都是 都是 的子集.则有 的子集.则有 (1)事件的包含(子事件)与相等 若 中的每一个样本点都在 中的每一个样本点都在 中,则称事件 中,则称事件 包含事件 包含事件 或称事件 或称事件 包含于事件 包含于事件 ( ( 为 为 的子事件),记作 的子事件),记作 ,或 ,或 .这时,事件 .这时,事件 出现,必然导致事件 出现,必然导致事件 出现. 出现. 若 且 且 ,则称事件 ,则称事件 与 与 相等,记作 相等,记作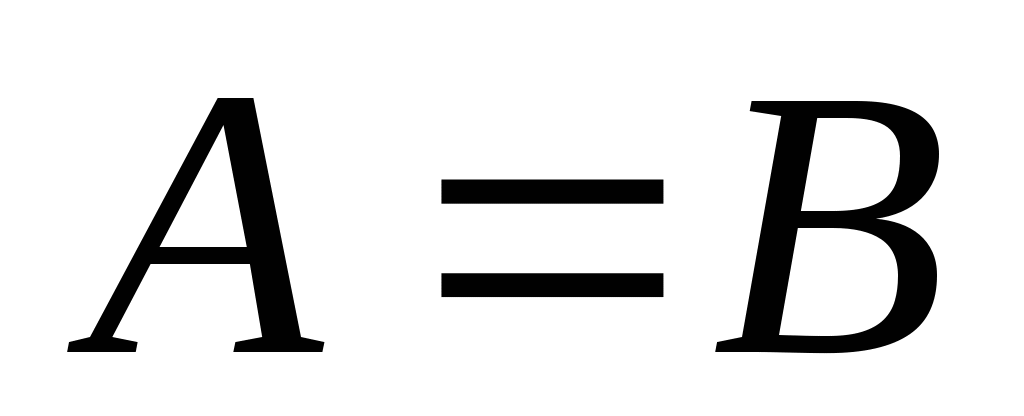 . . (2)事件的并(或和) 由 和 和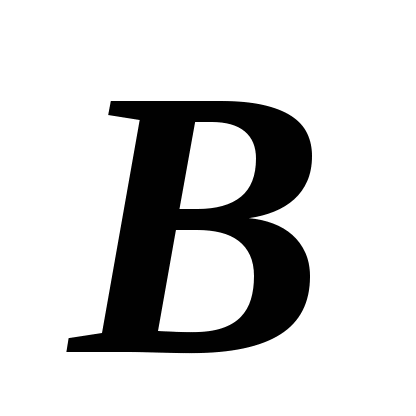 的所有样本点构成的集合,叫做 的所有样本点构成的集合,叫做 与 与 事件的并(或和)事件,记作(或 事件的并(或和)事件,记作(或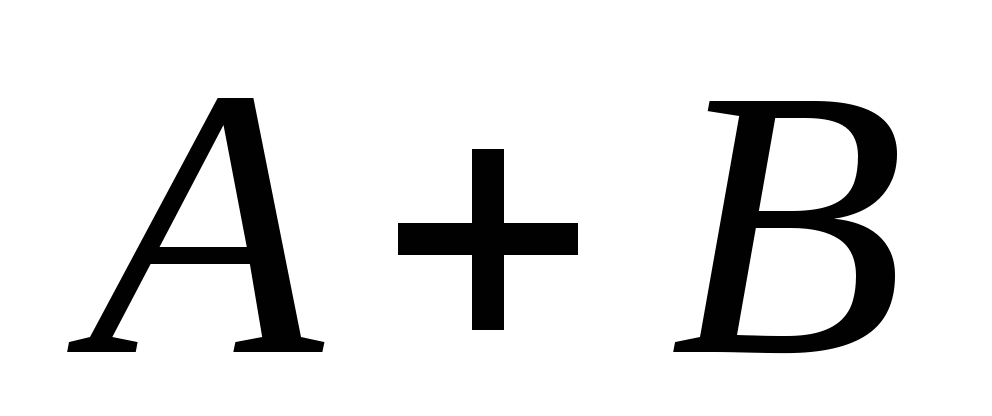 )即 )即 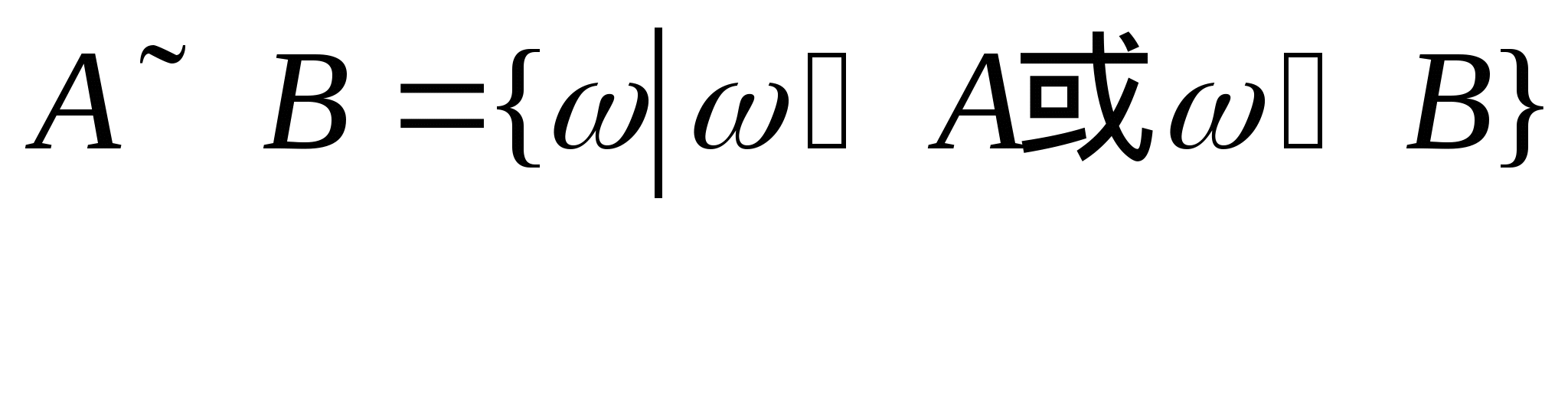 这时,事件 与 与 中至少有一个出现, 中至少有一个出现, 例如,甲、乙二人向同一目标进行一次射击,设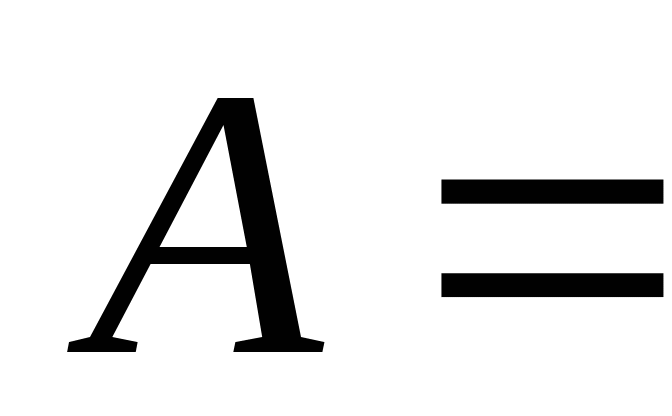 {甲击中目标}, {甲击中目标},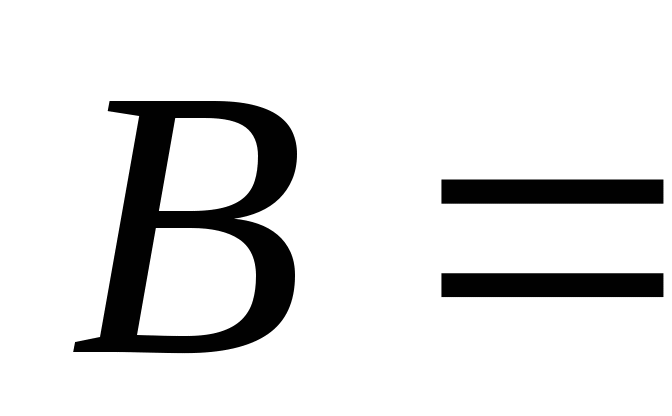 {乙击中目标}, {乙击中目标},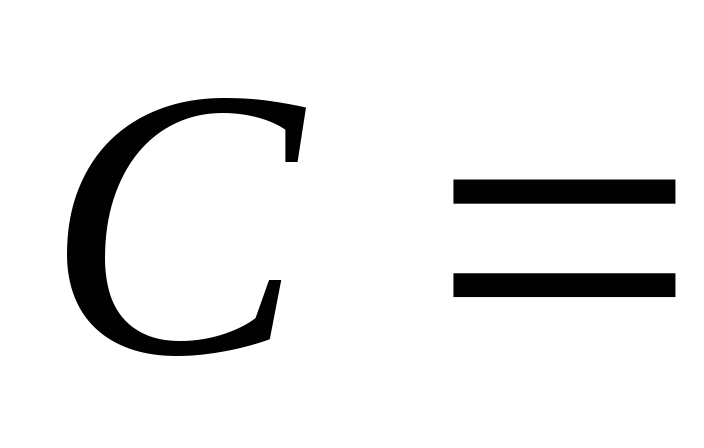 {目标被击中},则事件 {目标被击中},则事件 就是事件 就是事件 与 与 的并,即 的并,即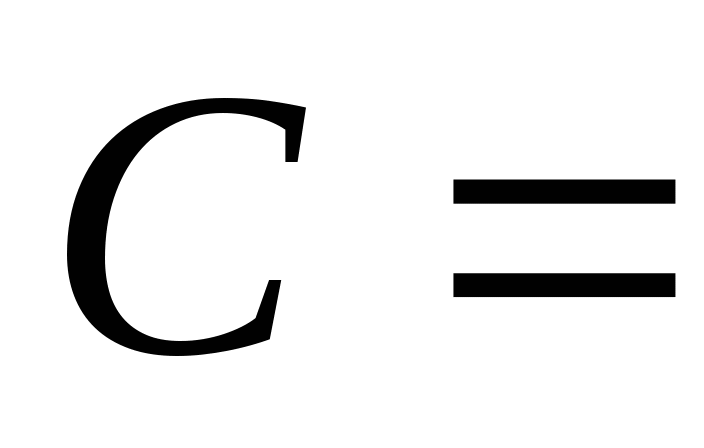  . . 显然事件的并有如下性质: (i) ; (ii) ; (ii)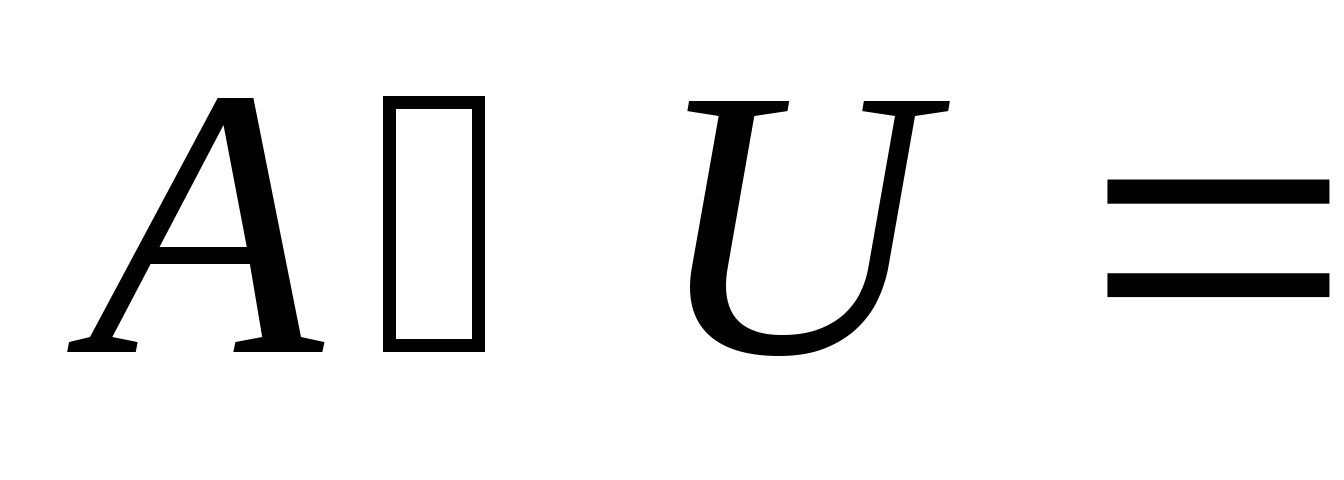  ; (iii) ; (iii)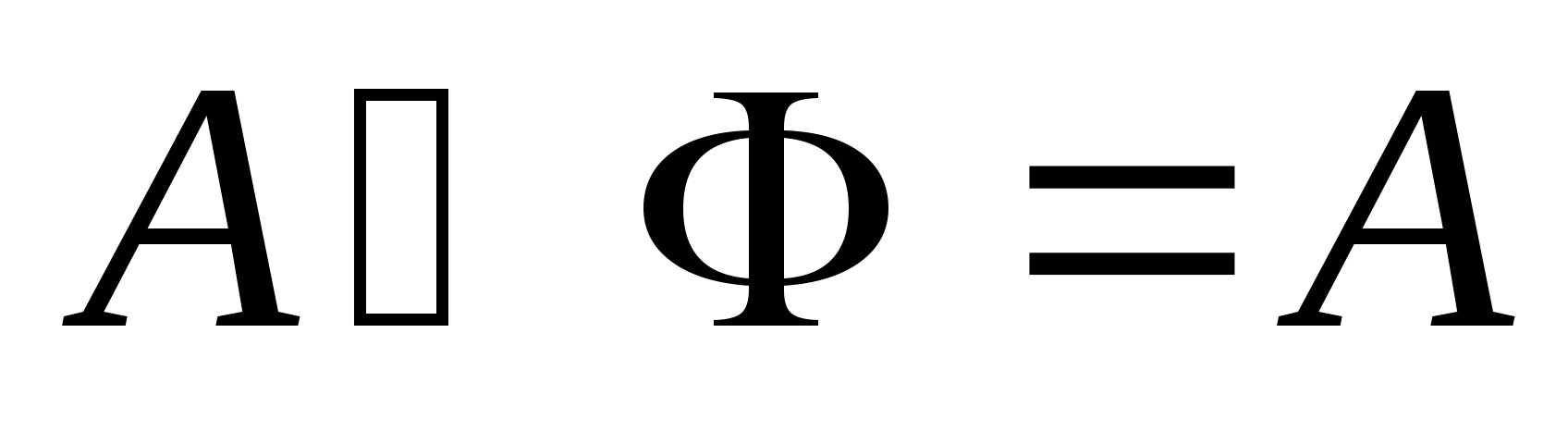 ; ; (iv)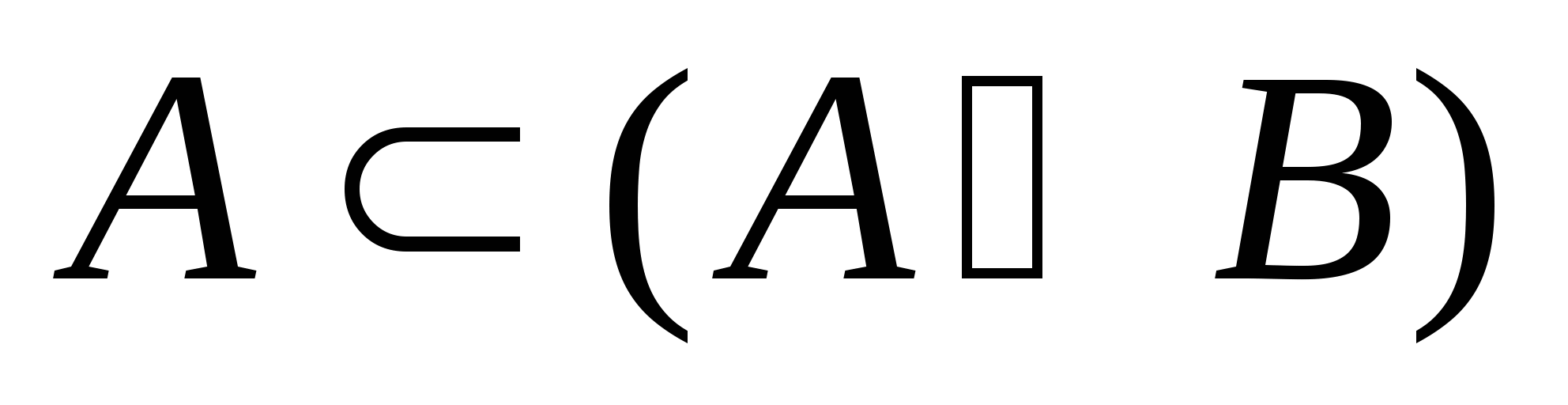 ; (v) ; (v)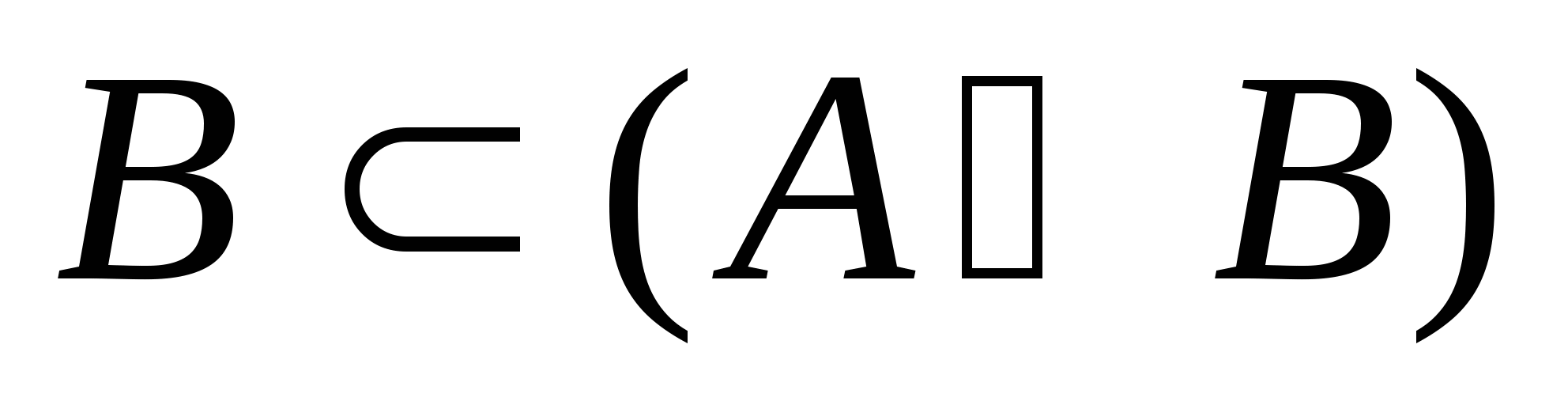 . . (3)事件的交(或积) 由同时属于 与 与 的样本点构成的集合叫做 的样本点构成的集合叫做 与 与 事件的交(或积),记作(或 事件的交(或积),记作(或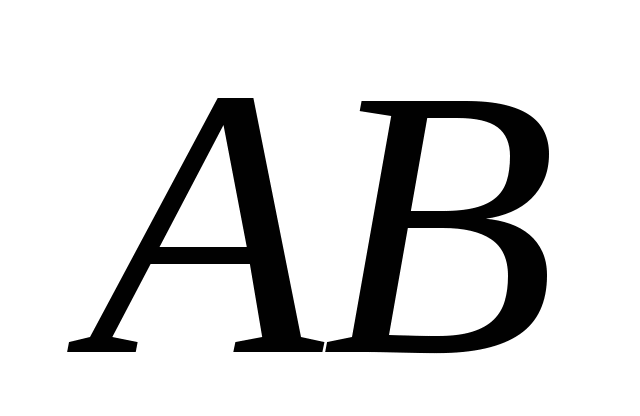 ),即 ),即 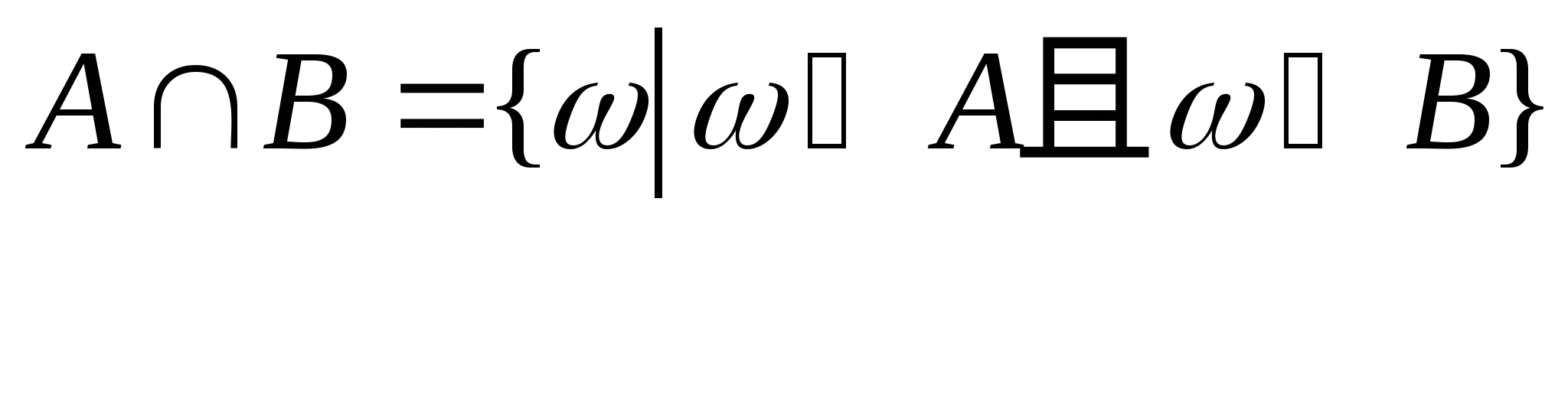 这时,事件 与 与 同时出现. 同时出现. 事件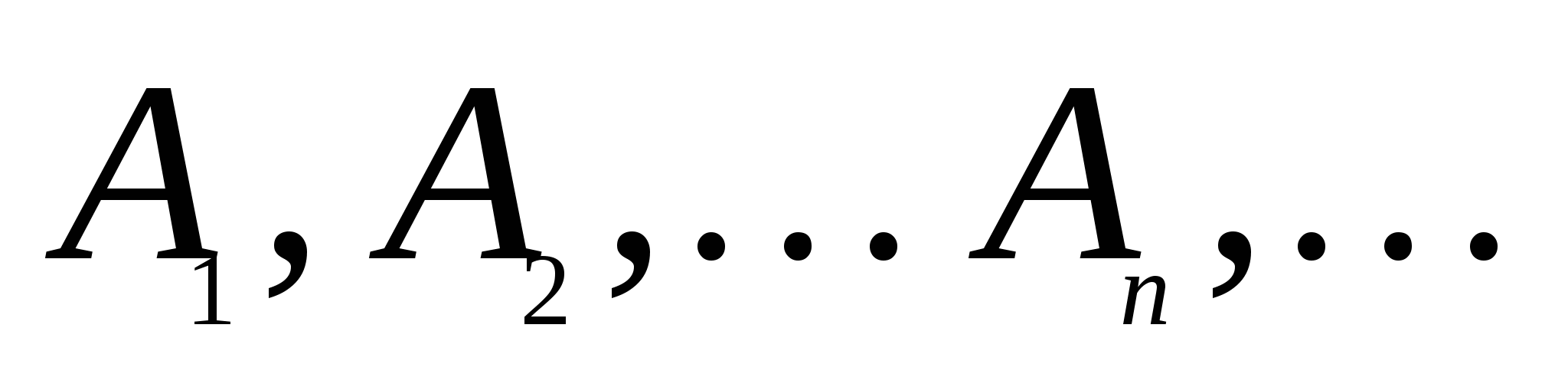 中至少有一个出现的事件为 中至少有一个出现的事件为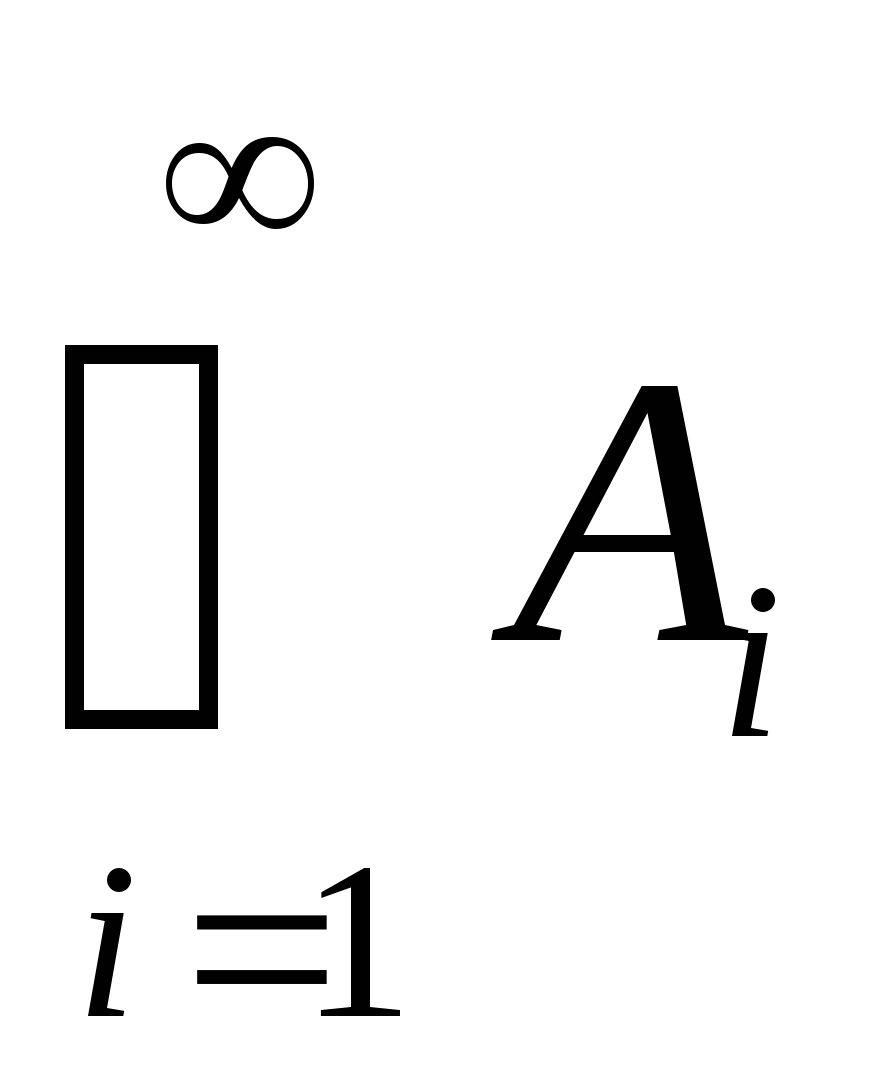 ;事件 ;事件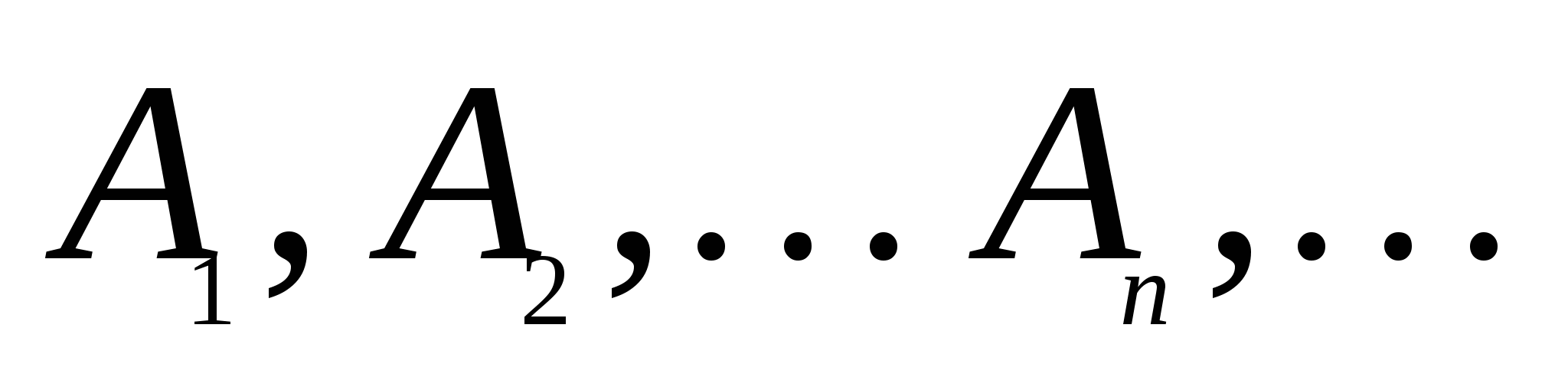 ,同时出现的事件为 ,同时出现的事件为 . . ( 4) 互不相容(或互斥)事件 若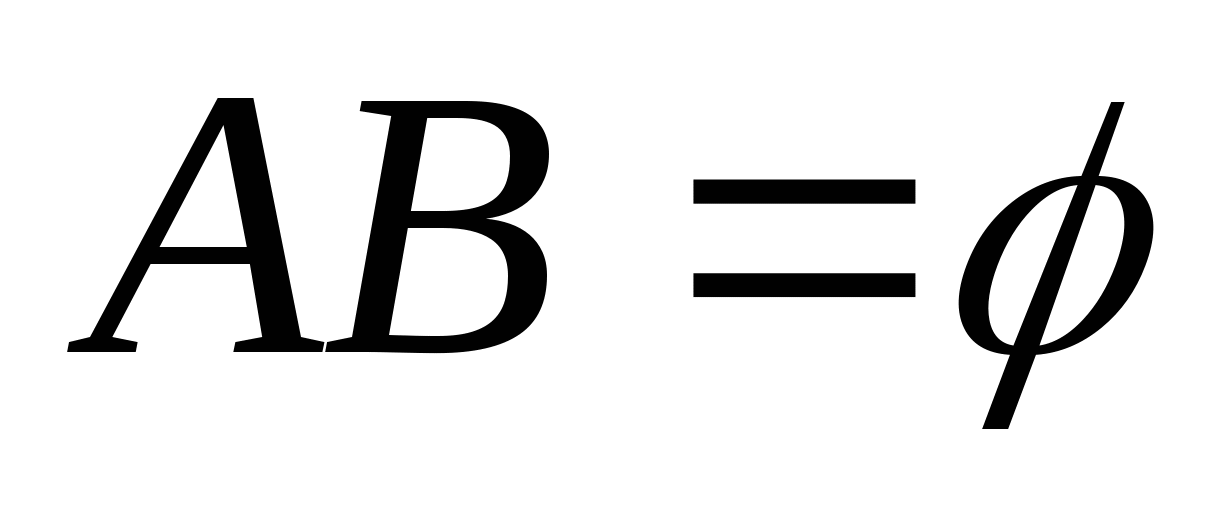 ,则称事件 ,则称事件 与 与 是互不相容(或互斥)的.这时,事件 是互不相容(或互斥)的.这时,事件 与 与 不能同时出现. 不能同时出现. 显然任一个试验E中,基本事件之间都是互不相容(或互斥)的. (5)互逆(或对立)事件 若  ,且 ,且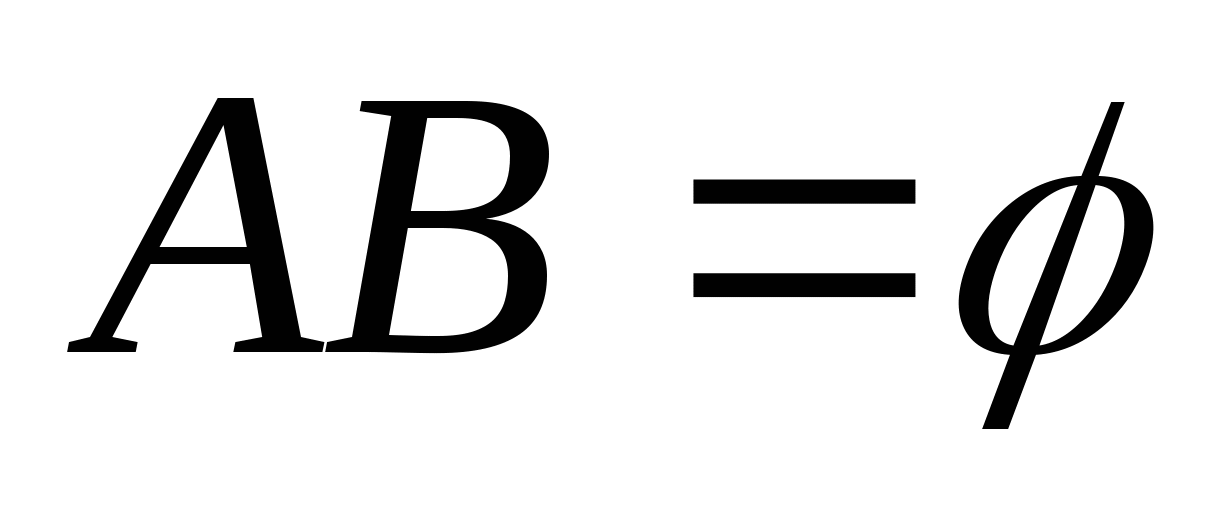 ,则称 ,则称 与 与 是互逆(或对立)事件,记作 是互逆(或对立)事件,记作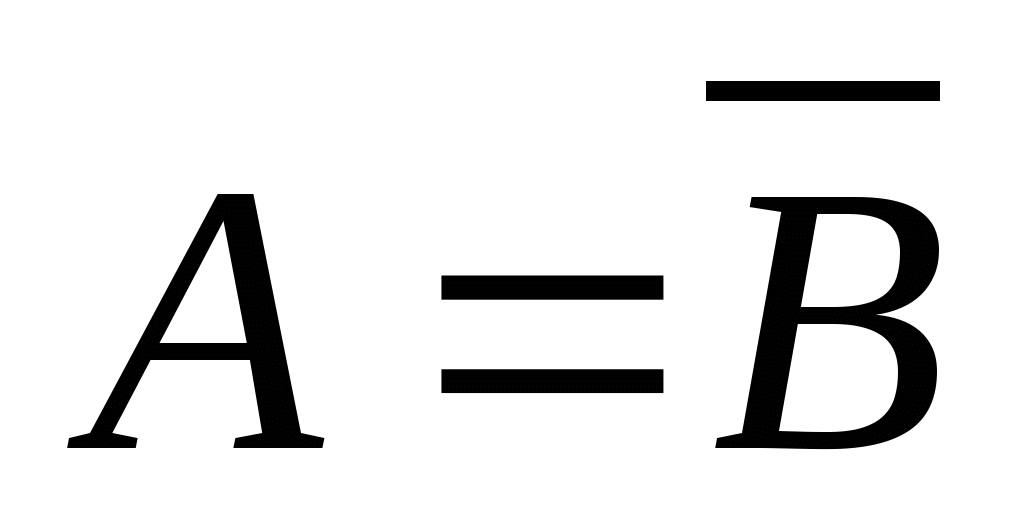 或 或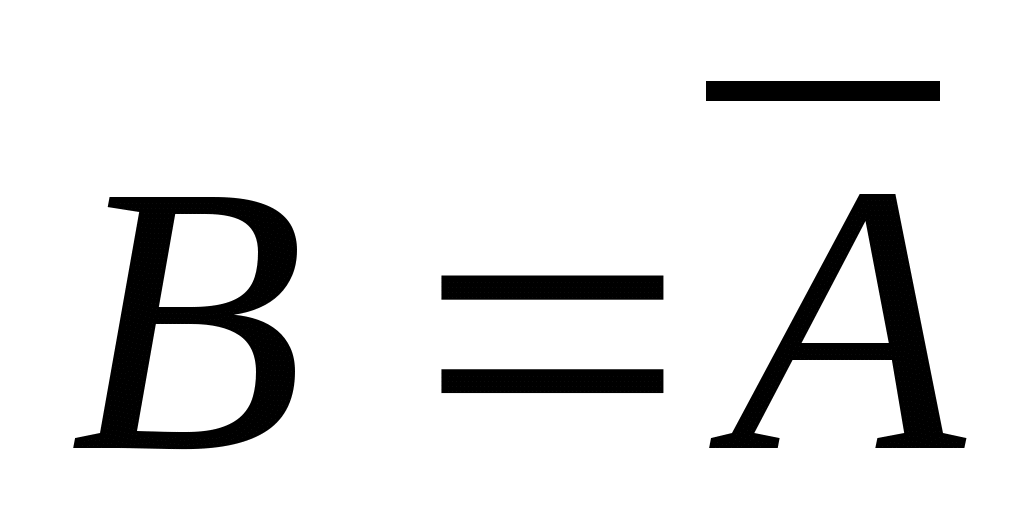 .一般地,事件 .一般地,事件 的逆事件记作 的逆事件记作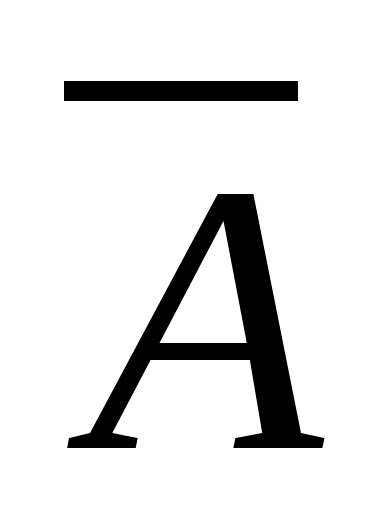 . . (6)事件的差 由所有属于 而不属于 而不属于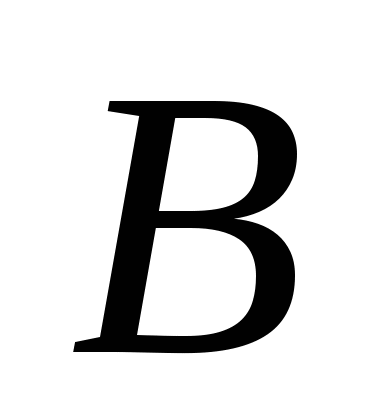 的样本点组成的集合,叫做 的样本点组成的集合,叫做 与 与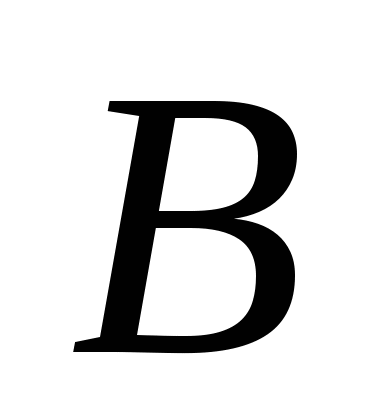 事件的差(简称差),记作 事件的差(简称差),记作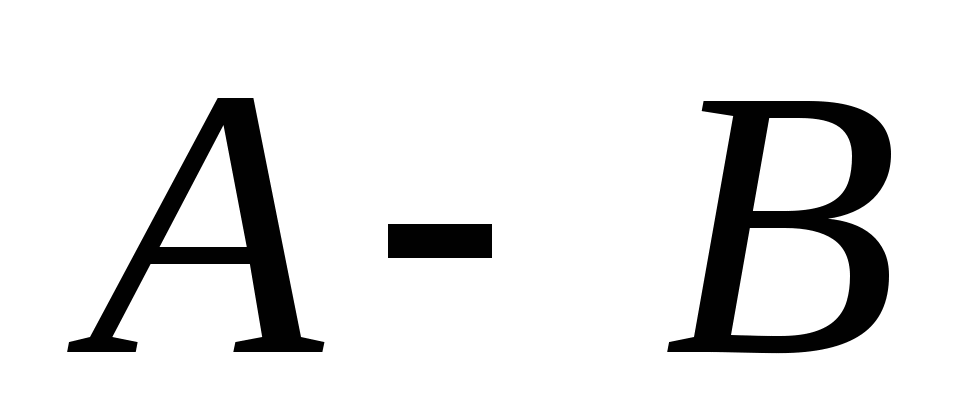 .即 .即 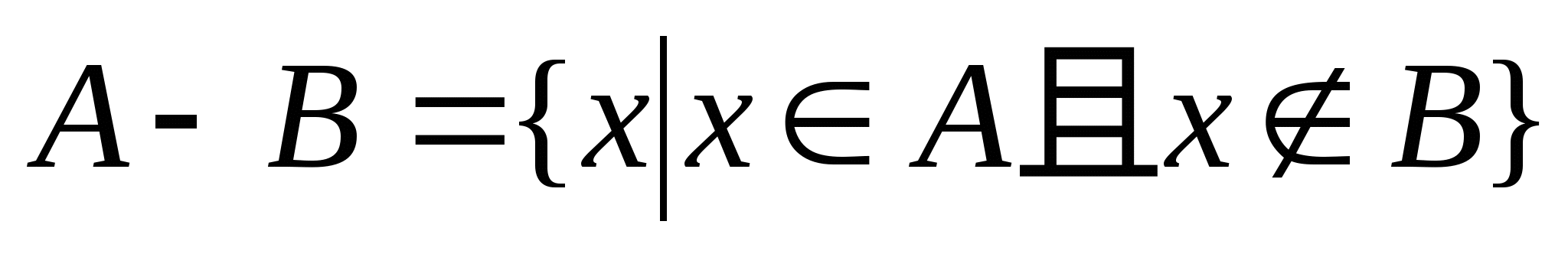 这时,事件 出现而事件 出现而事件 不出现.显然有 不出现.显然有 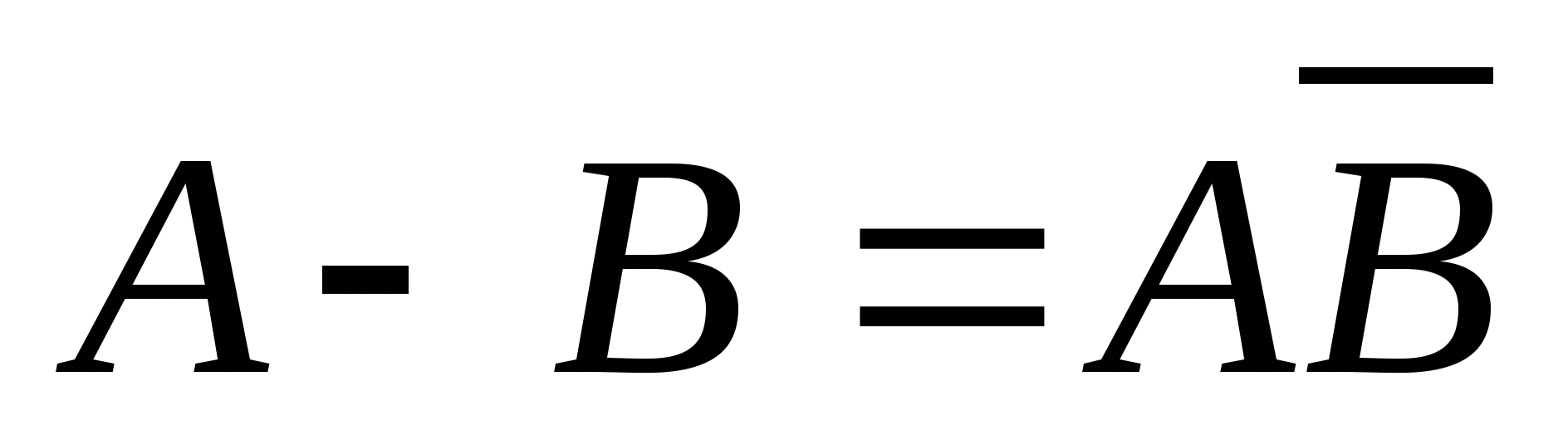 ,见图1-6. ,见图1-6. 由于事件是样本空间的子集,从而事件的运算与集合的运算完全一致,具有相同的性质如下: 交换律 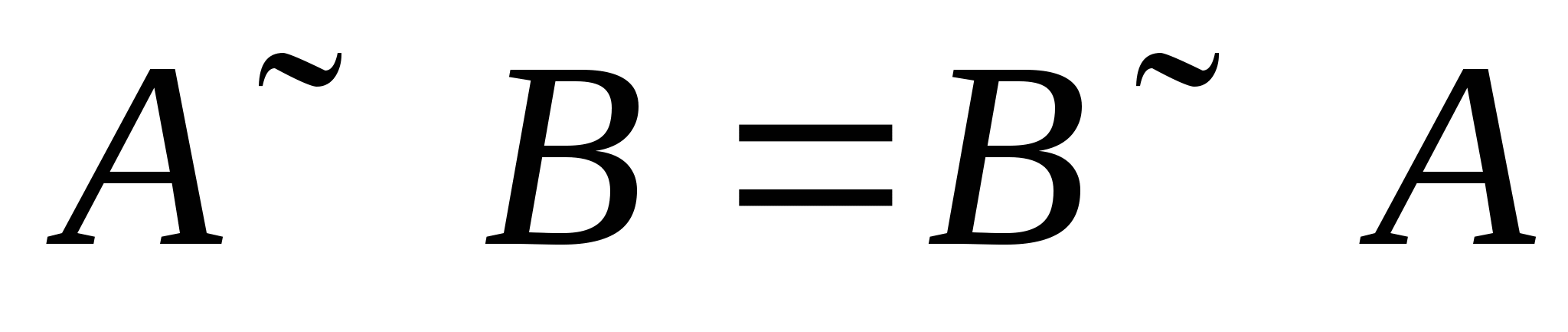 , ,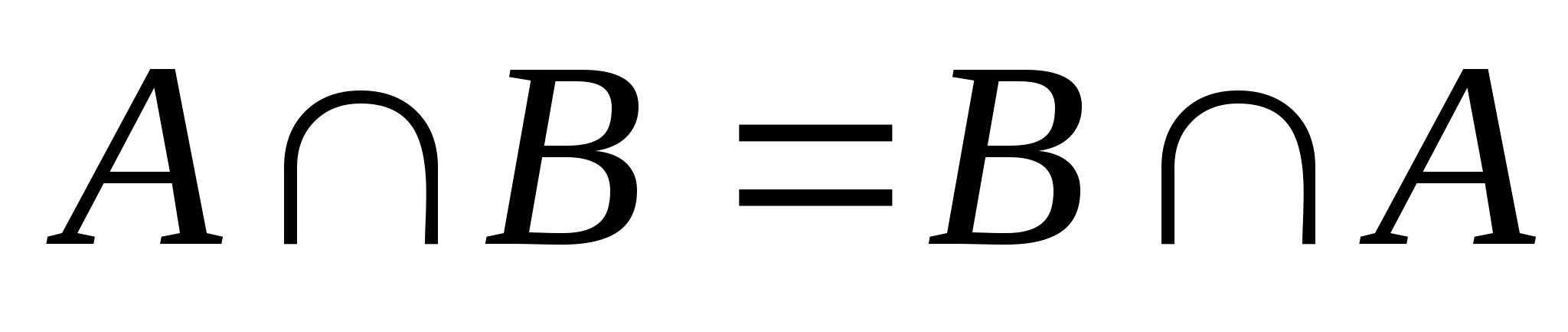 ; ; 结合律 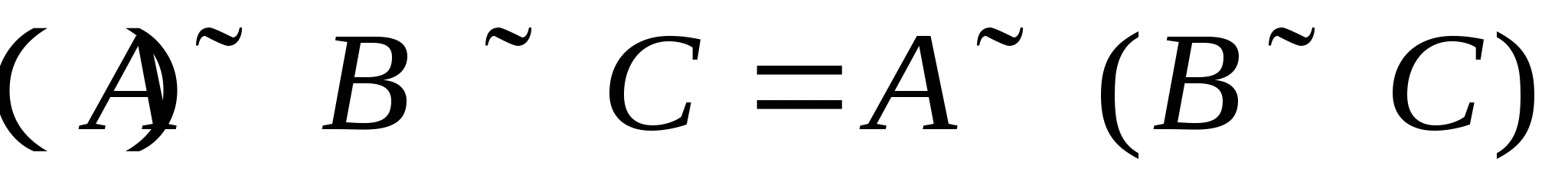 , ,
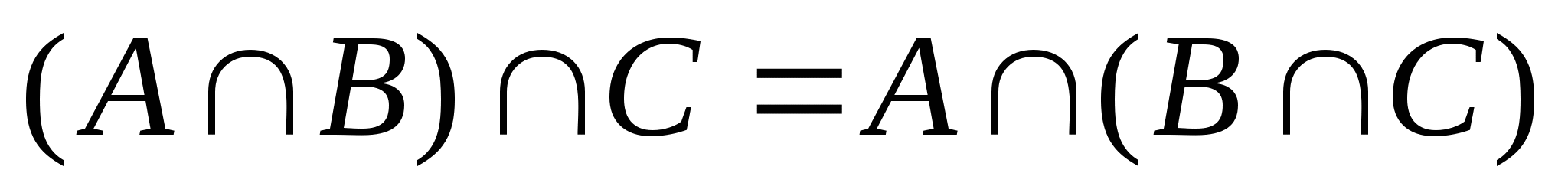 ; ;
分配律  , ,
 ; ;
(4) 对偶律 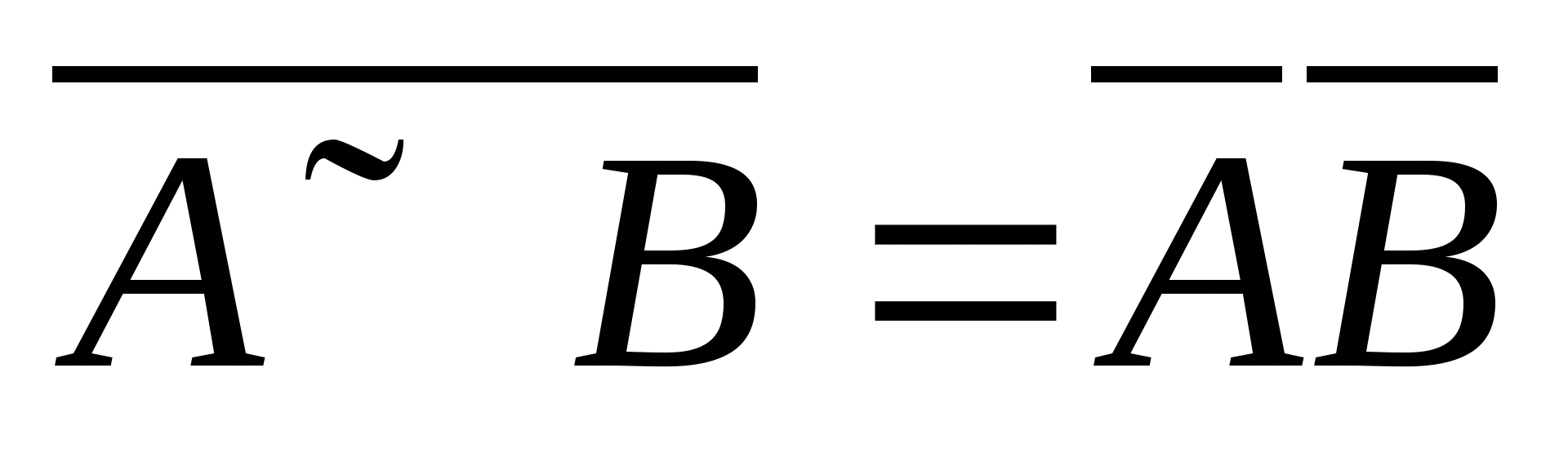 , , 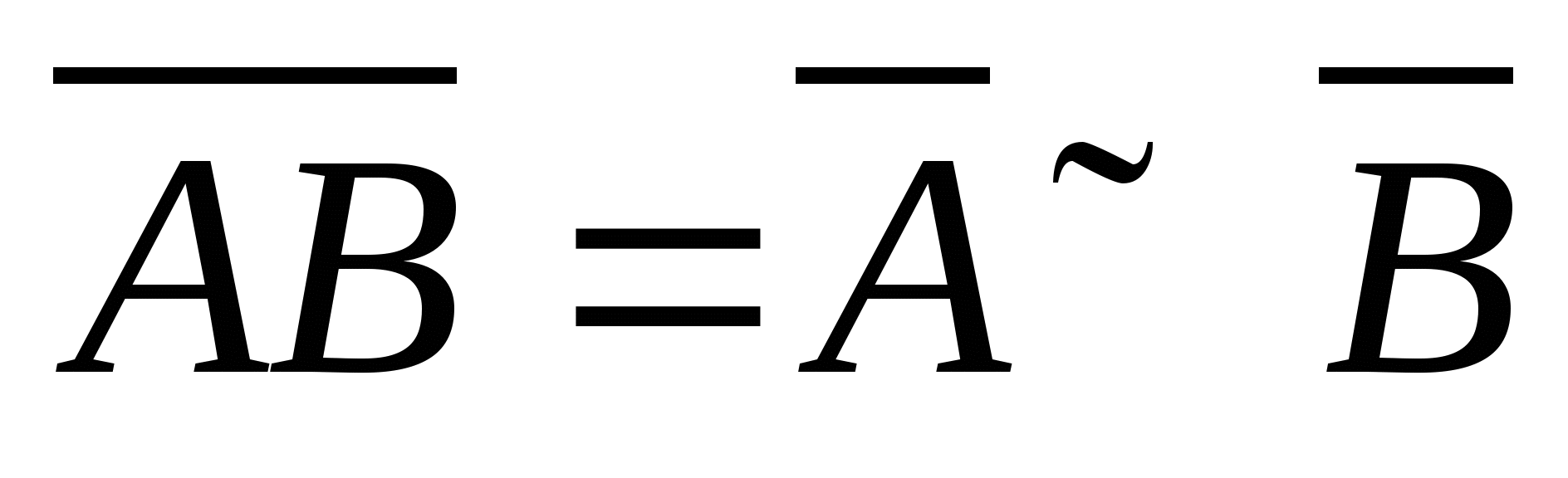 . . 对偶律可以推广到有限个以至可列个事件的情形,即  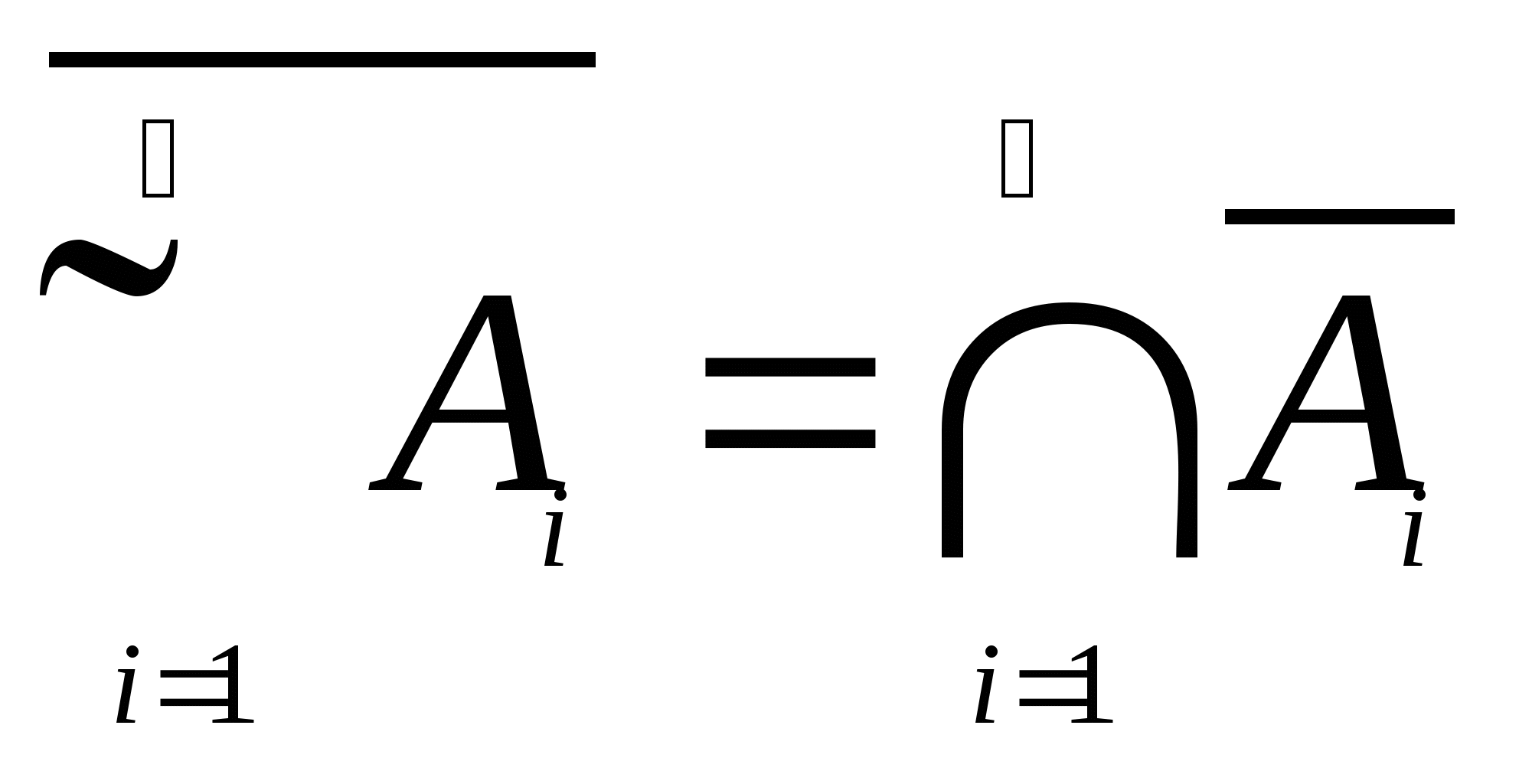 ; ; 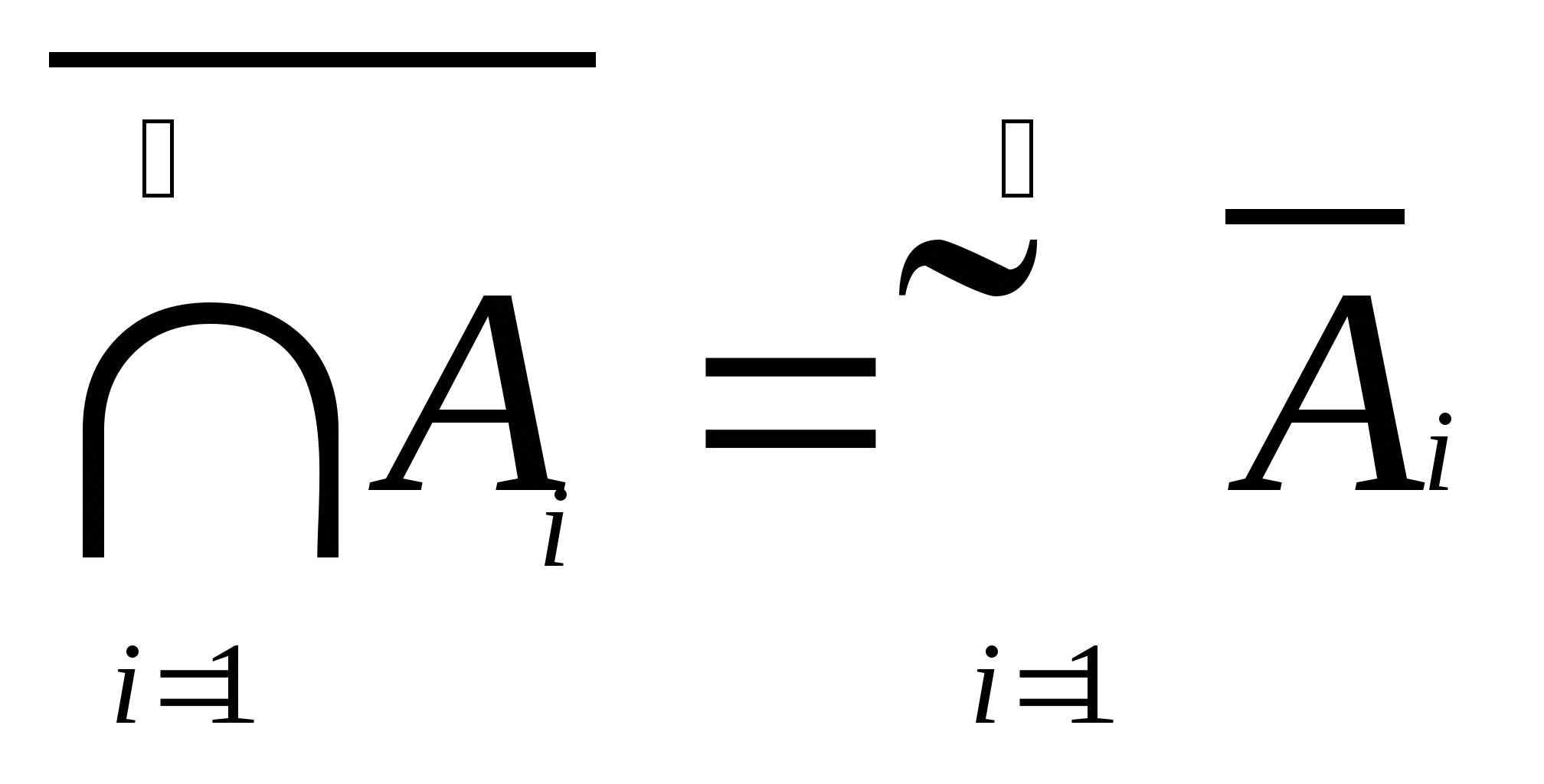 . .
例3 某射手向指定目标射击三枪,记 ,试用 ,试用 , , , , 表示下列各事件: 表示下列各事件: (1)只击中第一枪;(2)只击中一枪;(3)至少击中一枪. 第二节 随机事件的概率及其性质一、计数原理、排列与组合 1. 加法原理 若进行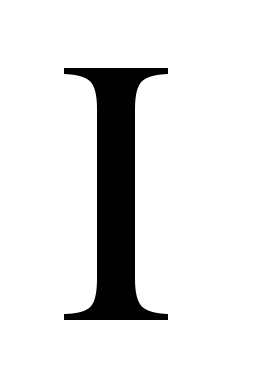 过程有 过程有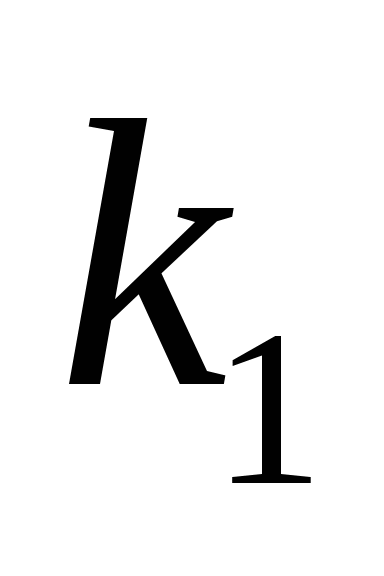 种方法,进行 种方法,进行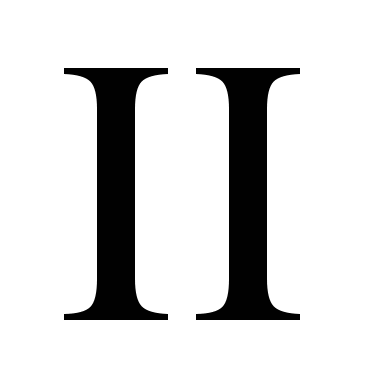 过程有 过程有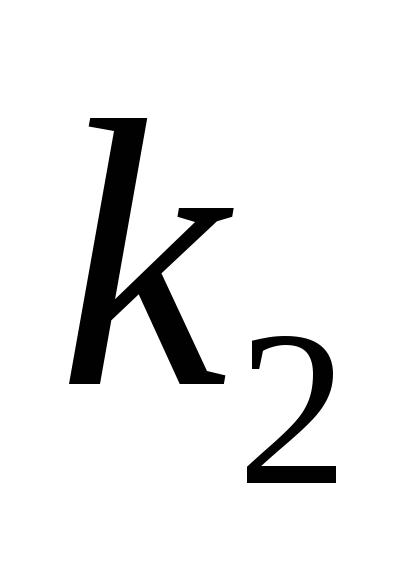 种方法,假定 种方法,假定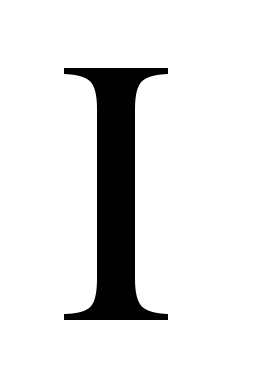 过程和 过程和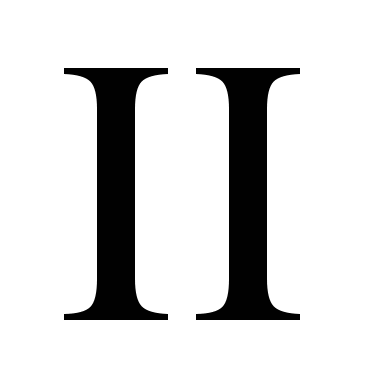 过程是并行的,则进行 过程是并行的,则进行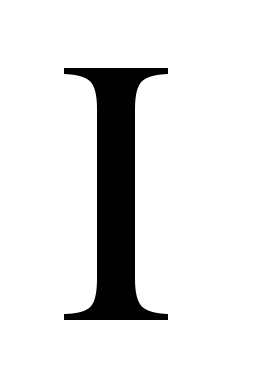 过程或 过程或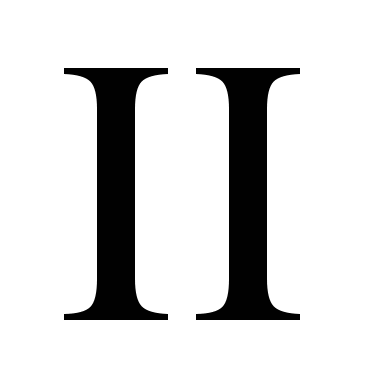 过程的方法共有 过程的方法共有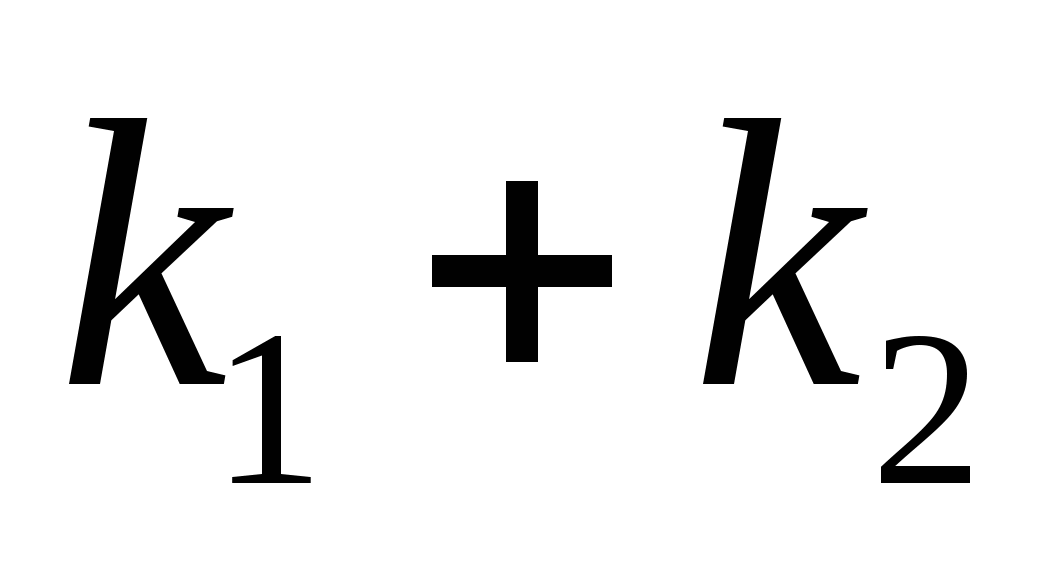 种. 种. 例如,若从甲地到乙地有2条公路,3条小路,则从甲地到乙地共有5种不同的走法. 乘法原理
若进行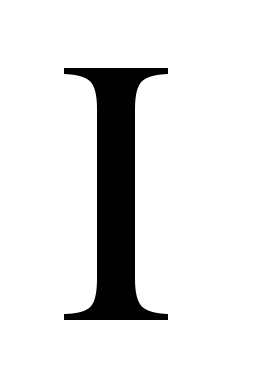 过程有 过程有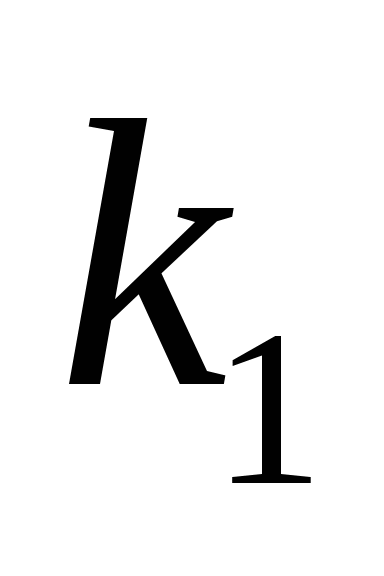 种方法,进行 种方法,进行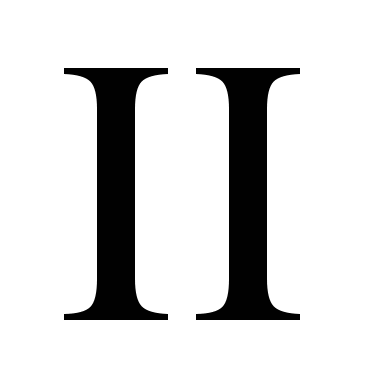 过程有 过程有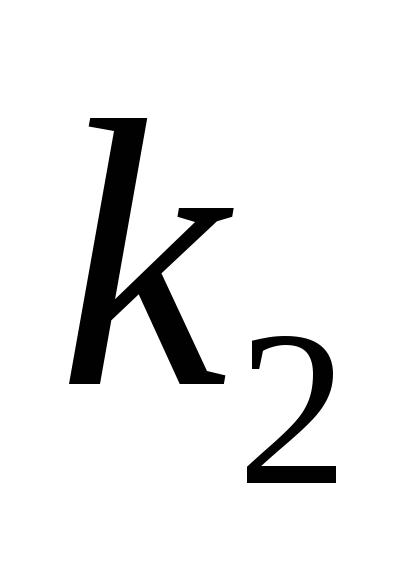 种方法,则进行 种方法,则进行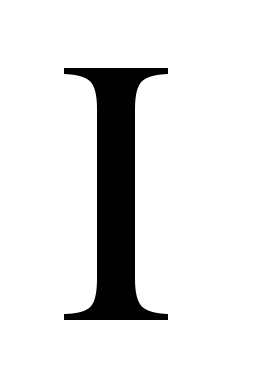 过程后再接着 过程后再接着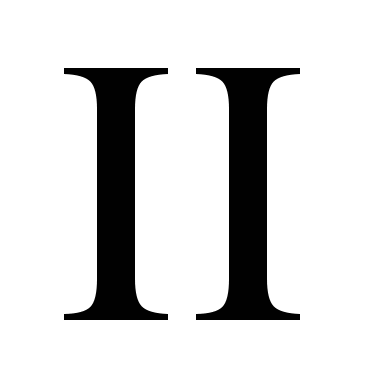 过程的方法共有 过程的方法共有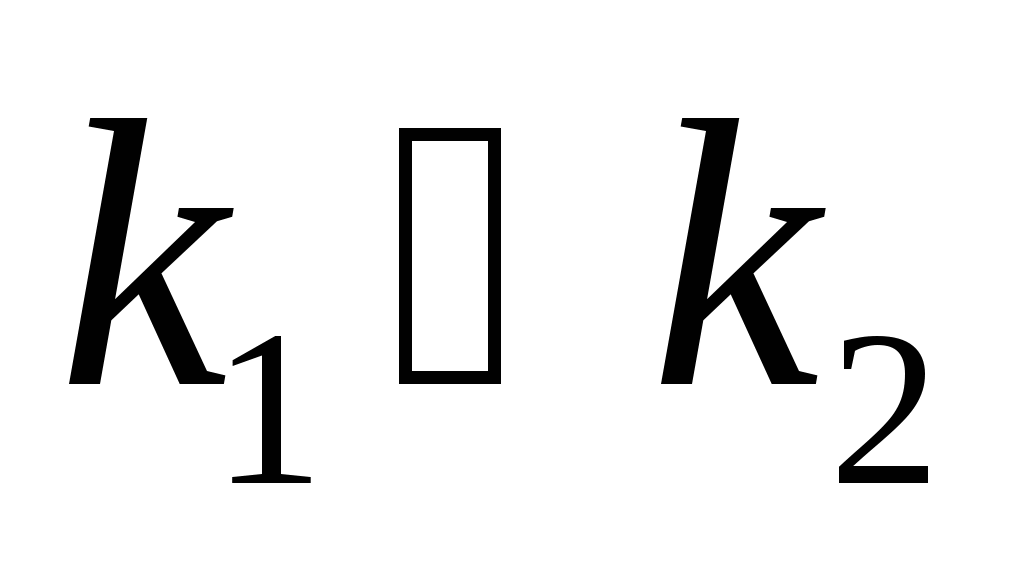 种. 种. 例如,若从甲地到乙地有2种走法,从乙地到丙地有3中走法,则从甲地到丙地共有不同的走法2×3=6. 上述两条原理可以推广到多个过程的情形. 3. 排列 从含有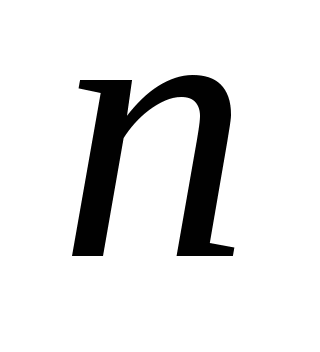 个元素的集合中任意取出r个元素进行排列,这时既要区别不同的元素又要考虑取出元素的顺序. 个元素的集合中任意取出r个元素进行排列,这时既要区别不同的元素又要考虑取出元素的顺序. (1)在有放回选取的情形 这时每一次取出都是在全体元素中进行的,同一元素可能被重复取出.从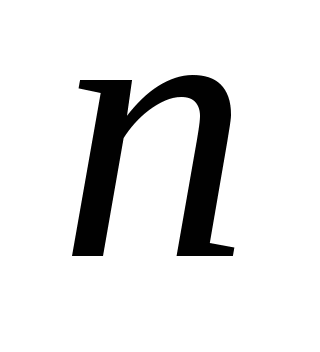 个元素中有放回地取出r个元素所构成的排列叫做有重复的排列,其总数共有 个元素中有放回地取出r个元素所构成的排列叫做有重复的排列,其总数共有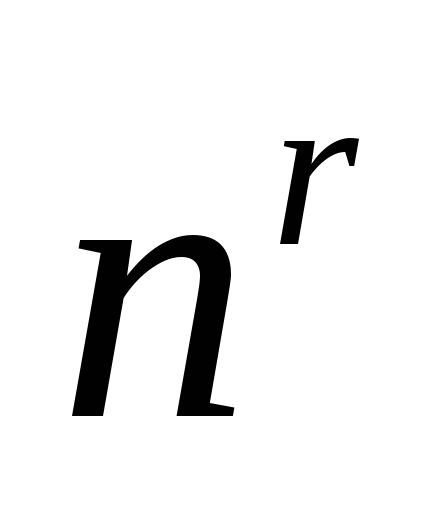 . . (2) 在不放回选取的情形,这时一个元素一旦被取出便立刻从该集合中出去,因此每个元素至多被取到一次.从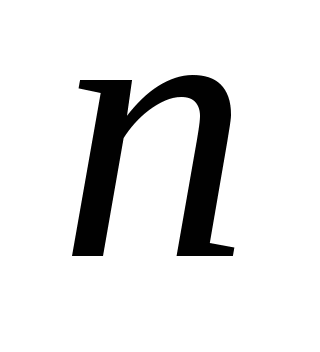 个元素中不放回地取出r个元素所构成的排列叫做选排列,其总数为 个元素中不放回地取出r个元素所构成的排列叫做选排列,其总数为 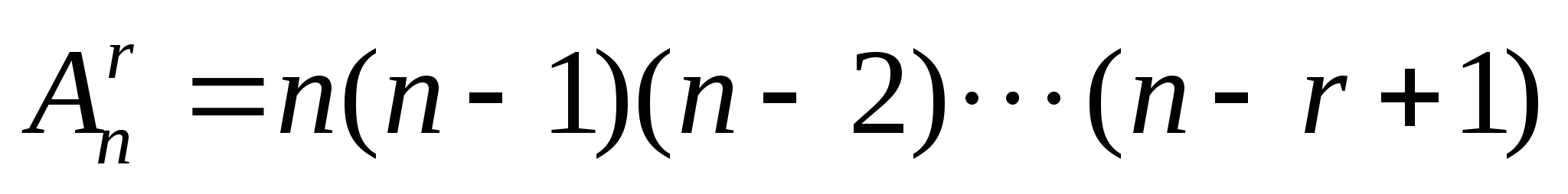
特别地,当r=n时,叫做全排列,总数为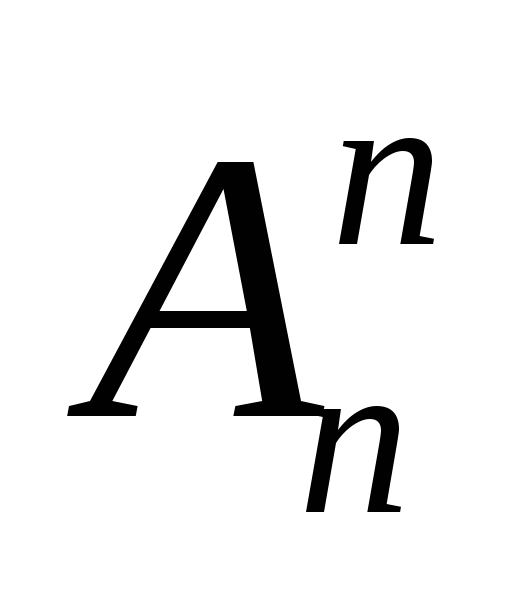 =n! =n! 4. 组合 从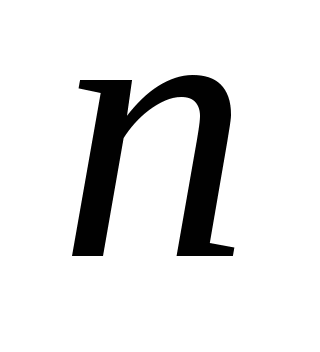 个元素中任意取出r个元素而不考虑顺序,叫做组合,其总数为 个元素中任意取出r个元素而不考虑顺序,叫做组合,其总数为  . .
(这里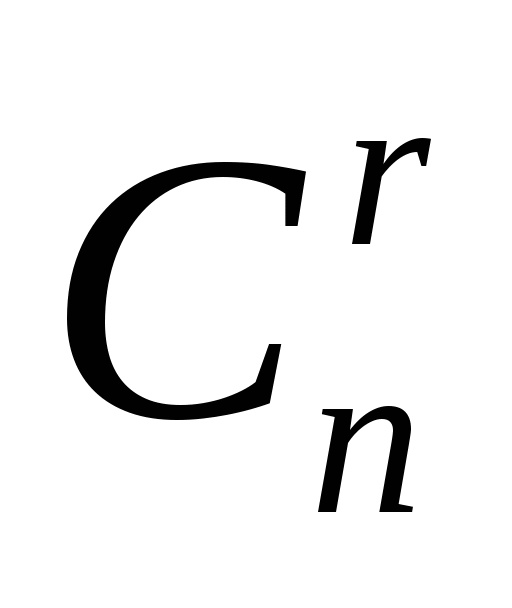 是二项展开式 是二项展开式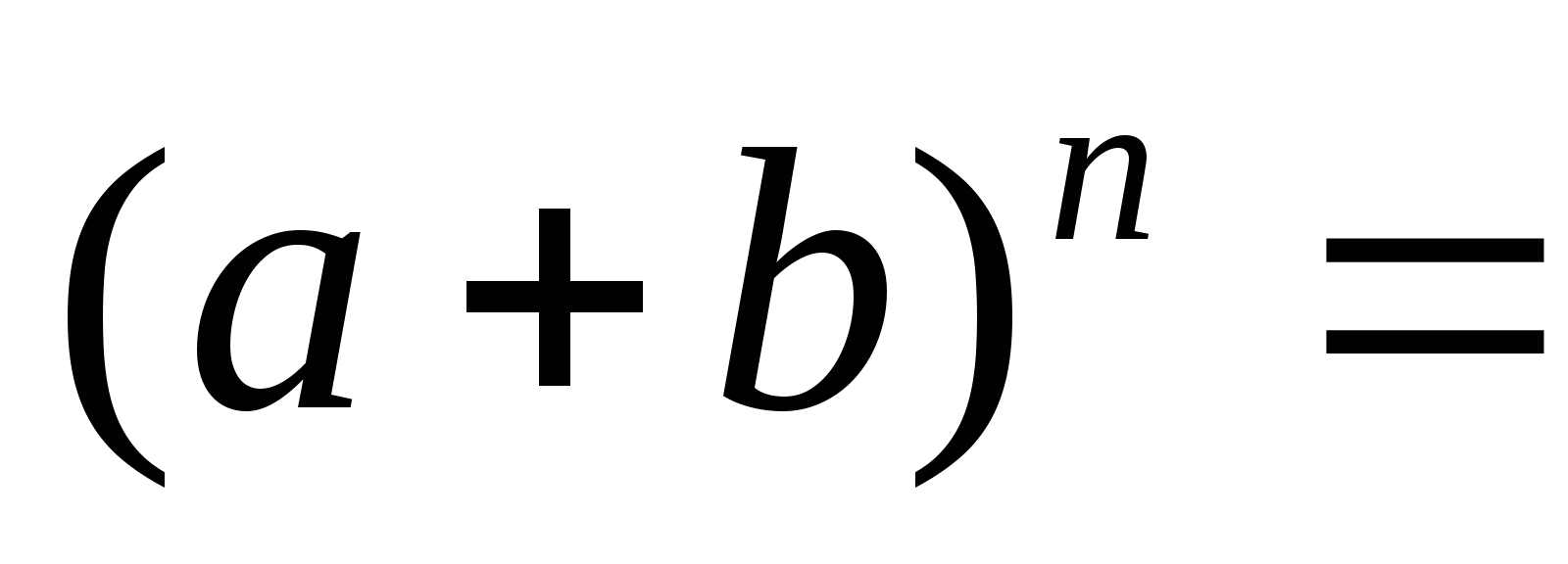 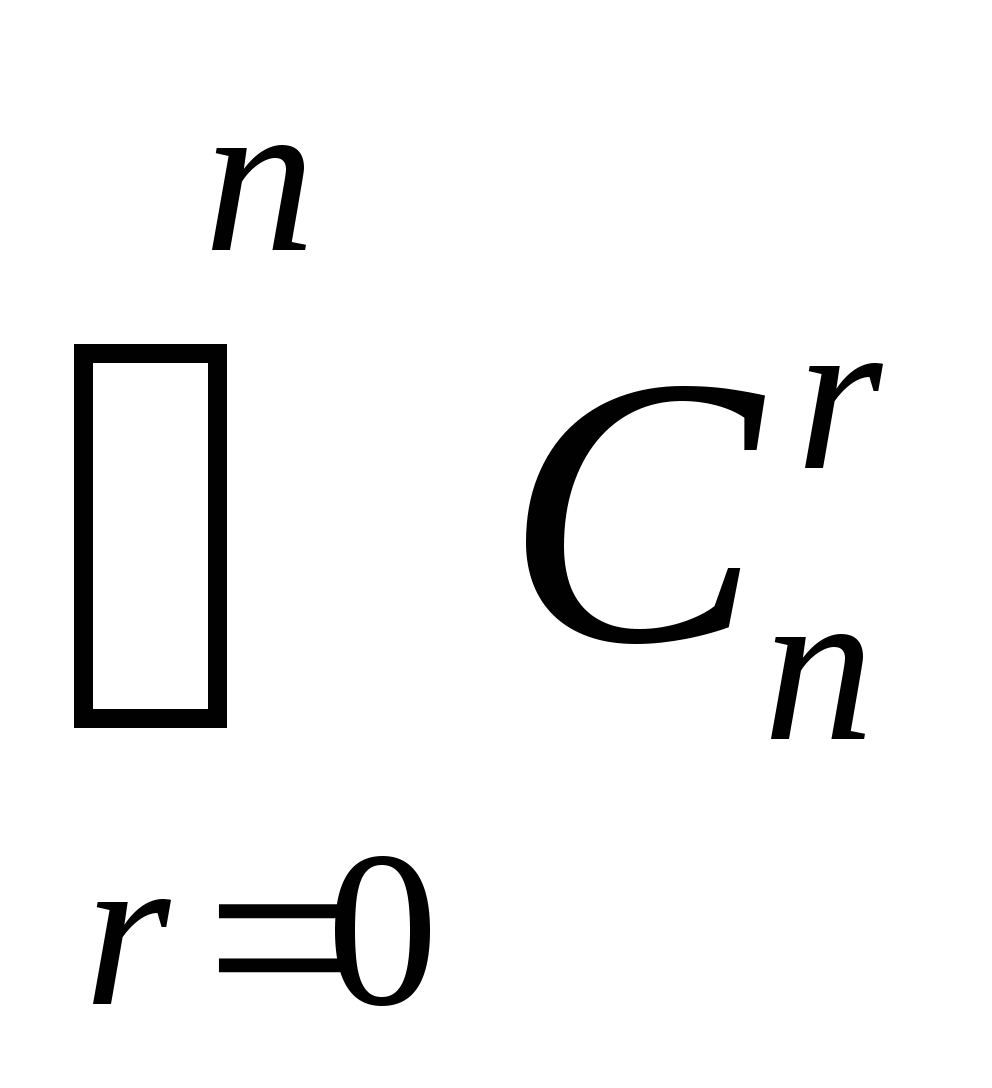 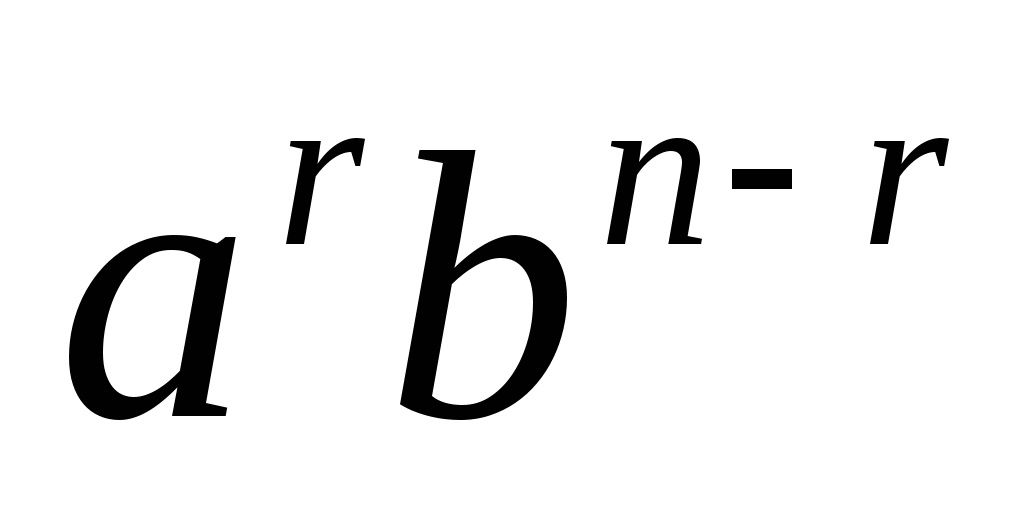 的的系数). 的的系数). 例如,一罐中装有4个白球,3个黑球,从这7个球中任意取3个球的总数为 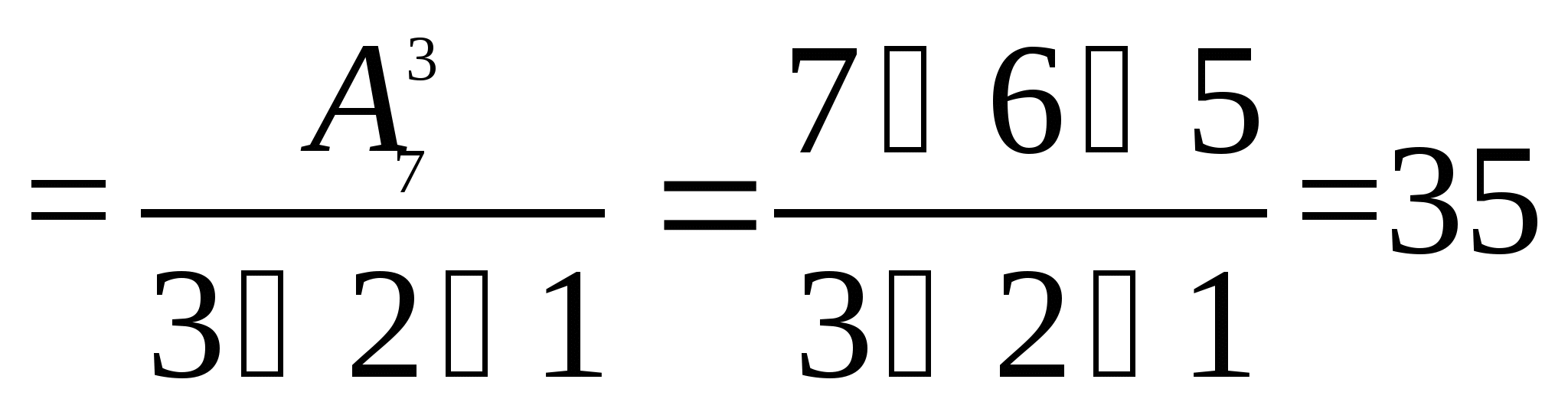 . . 二、事件的频率及其性质 定义1 随机事件 在 在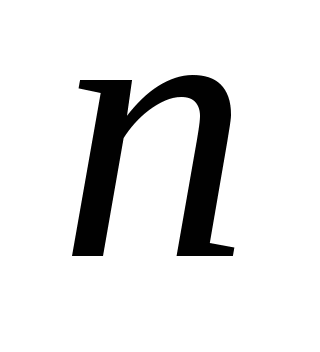 次重复试验中发生了 次重复试验中发生了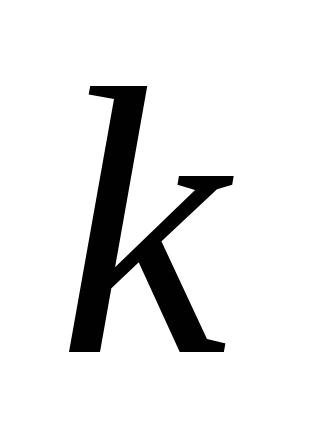 次,则称比值 次,则称比值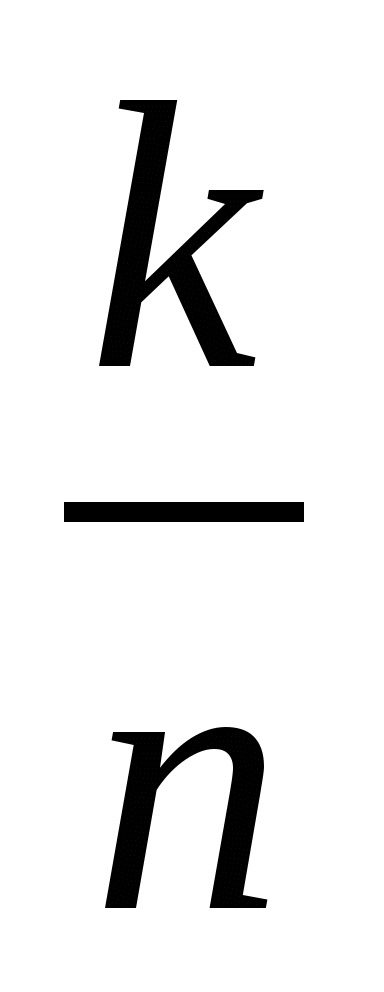 为事件 为事件 在 在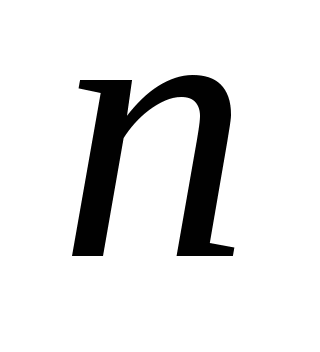 次试验中出现的频率,记为 次试验中出现的频率,记为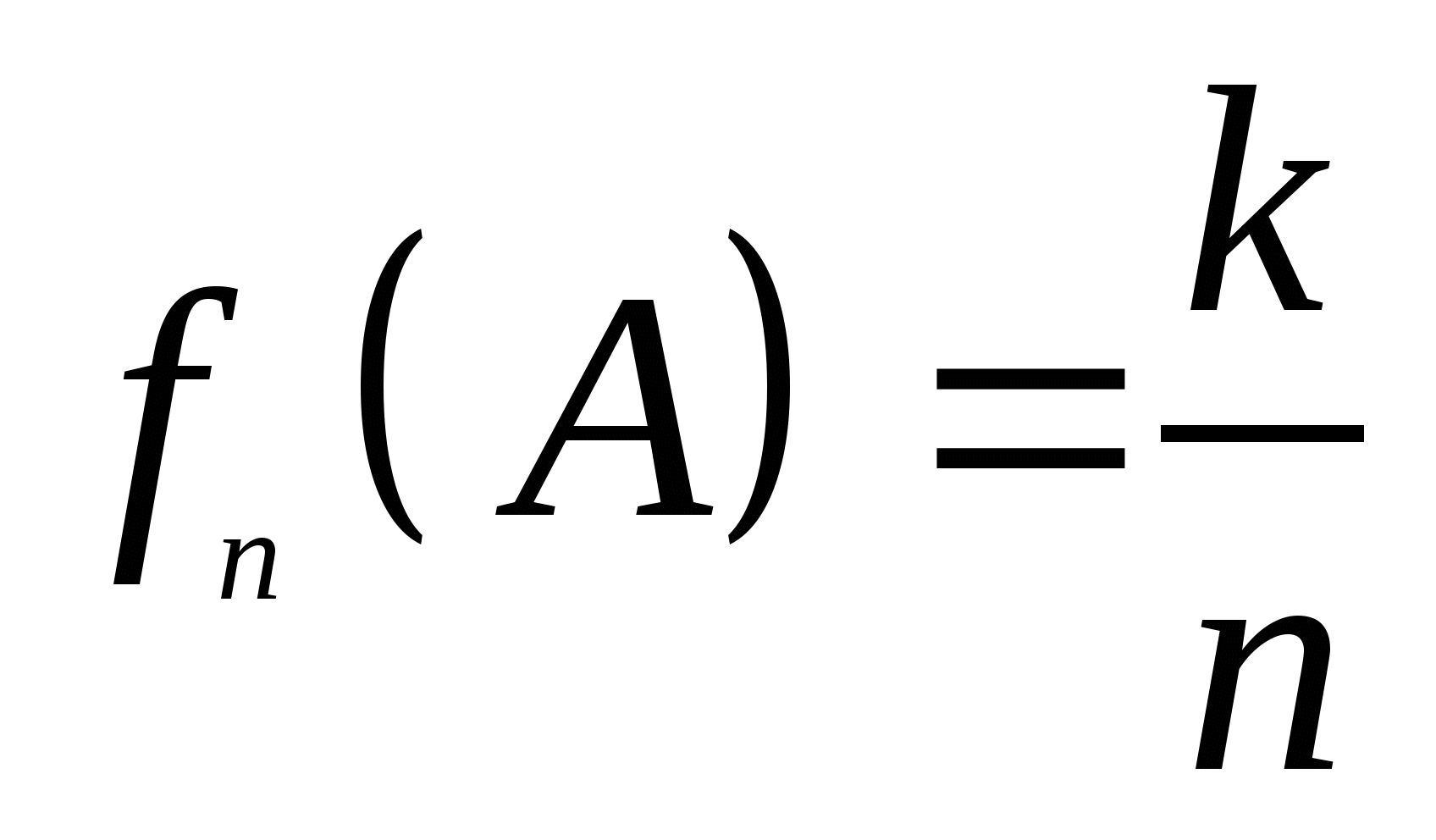 . . 由此定义,容易得到频率具有如下性质: (1) 对于每一个随机事件A,有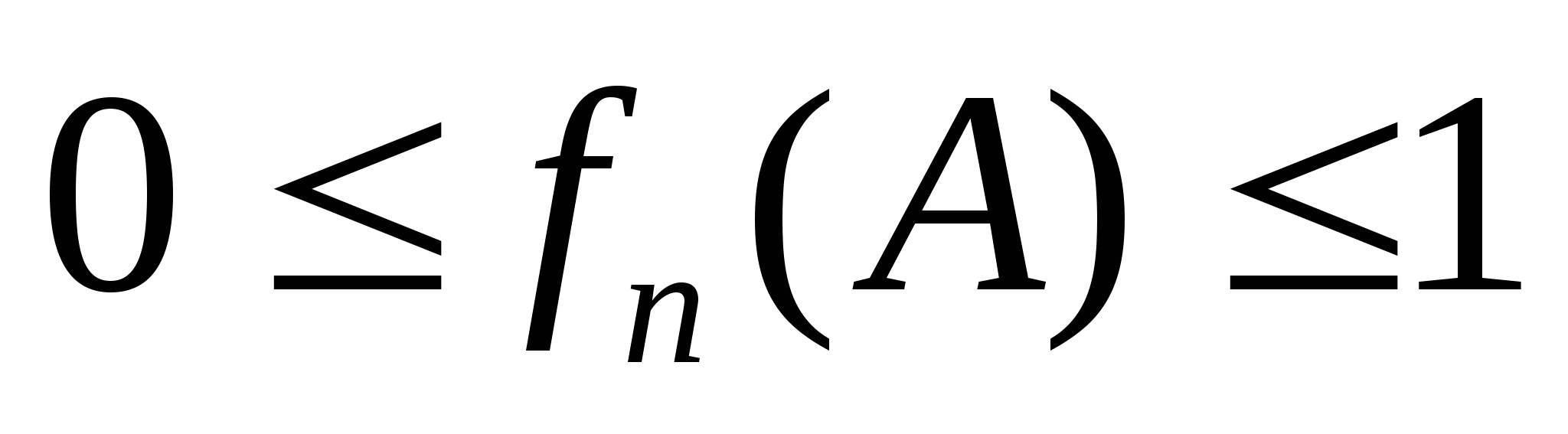 ; ; (2)  , ,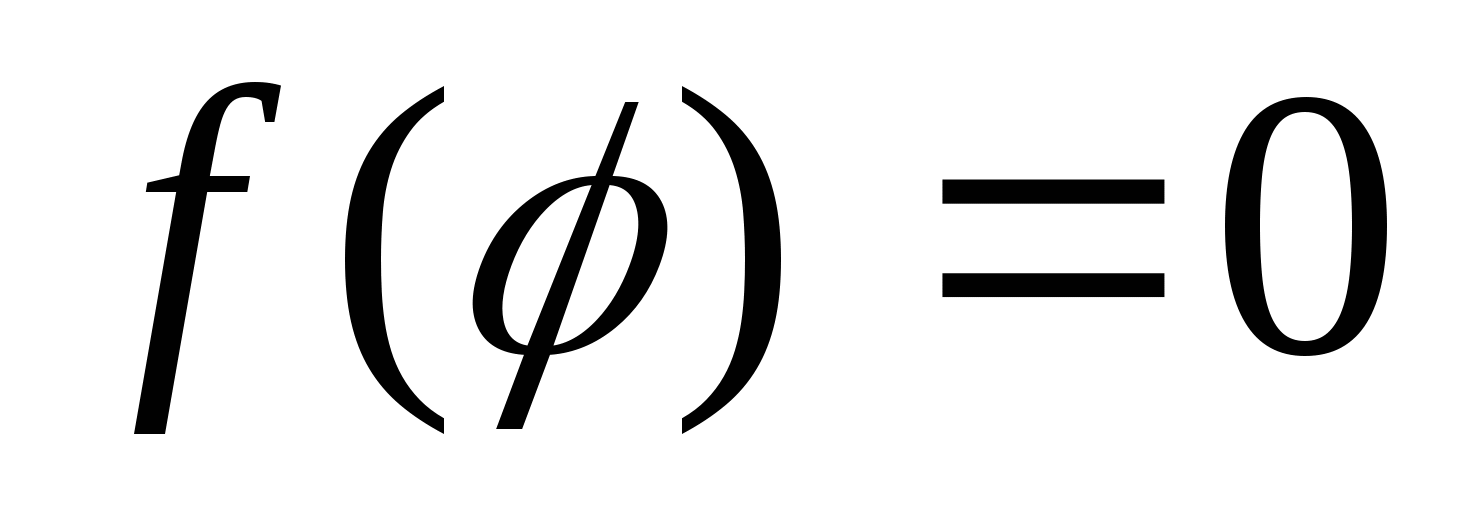 ; ; (3) 若事件 , , 互不相容,则有 互不相容,则有 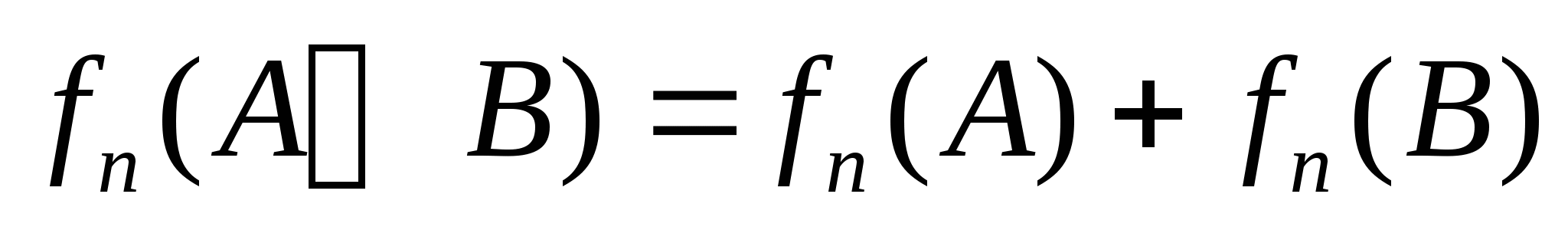
性质(3)叫做频率的可加性.其证明如下: 设在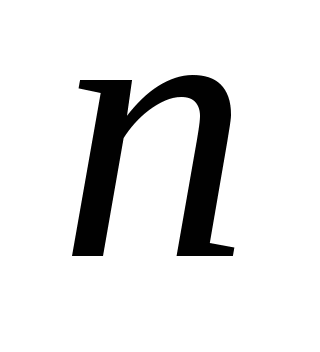 次试验中,事件A、B、 次试验中,事件A、B、 ,分别出现 ,分别出现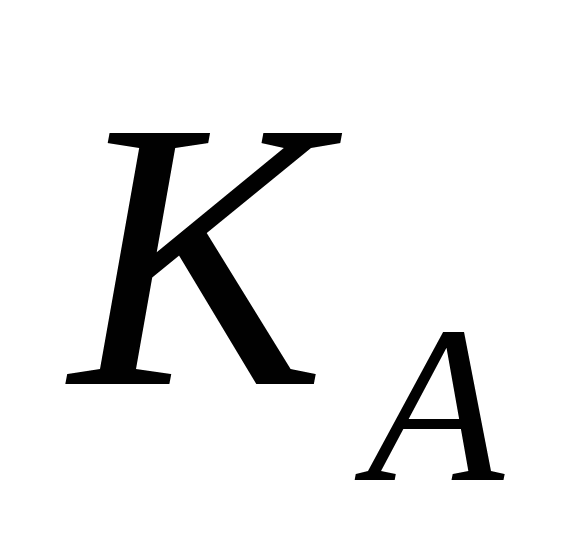 次, 次,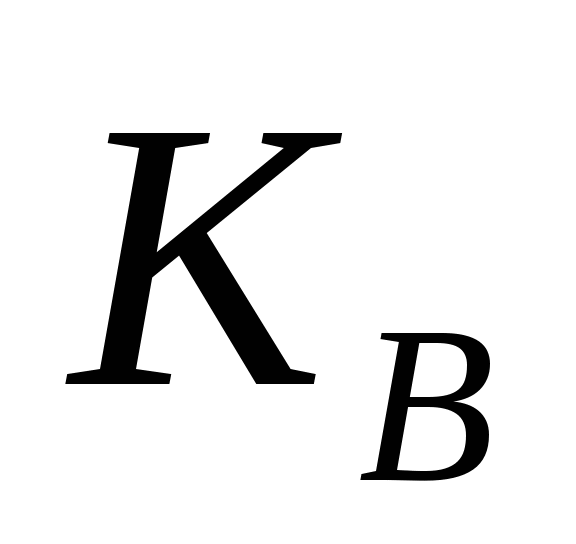 次, 次,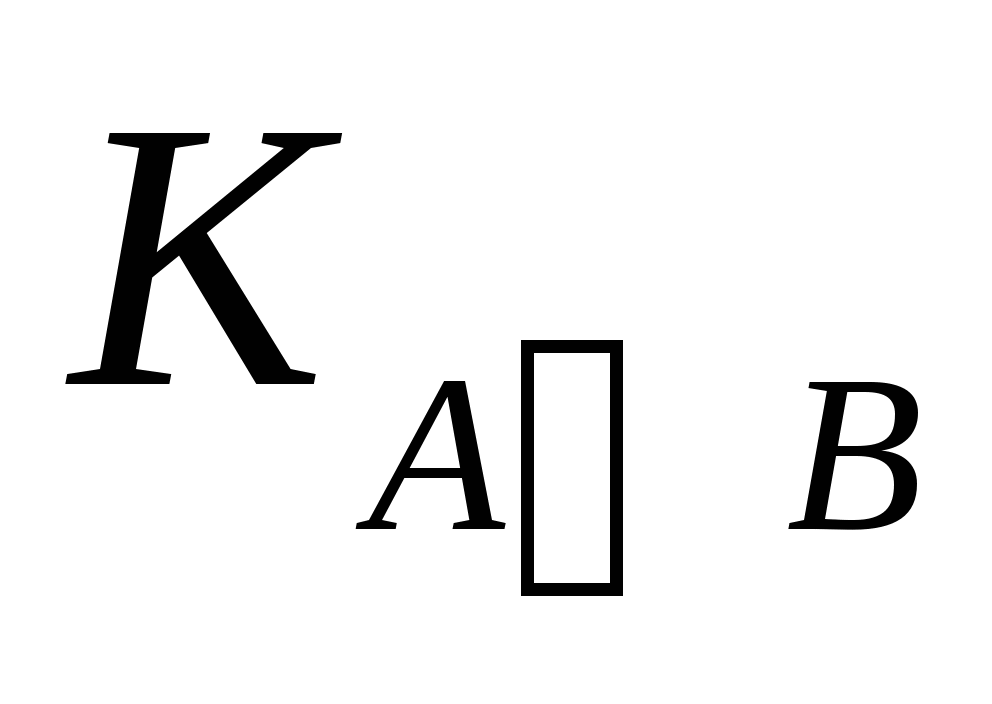 次,因为 次,因为 、 、 互不相容,所以 互不相容,所以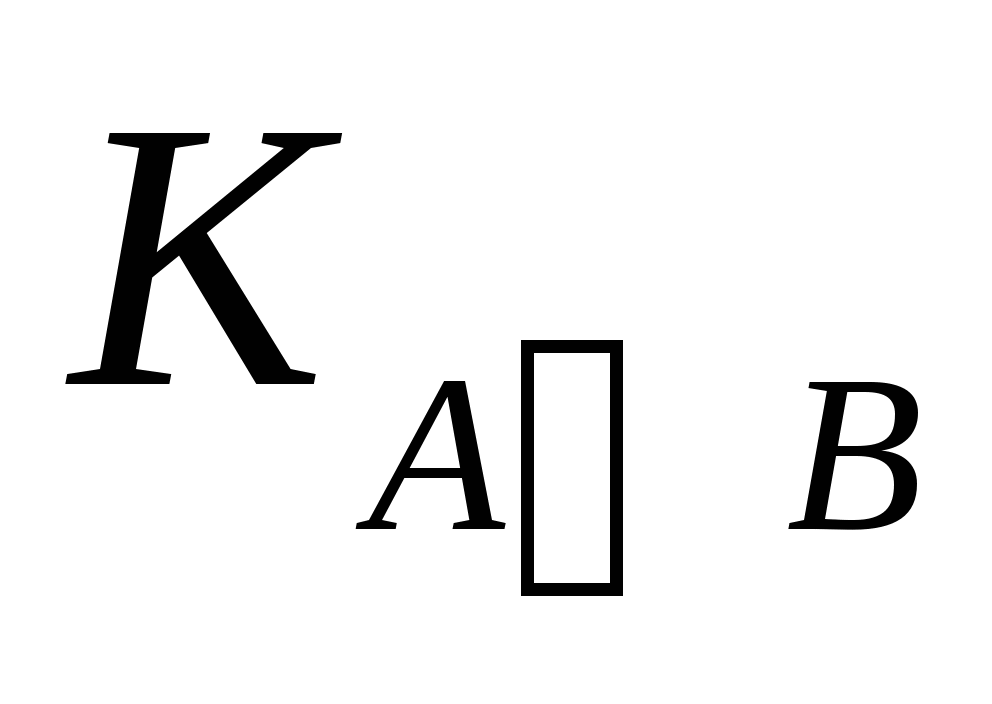 = =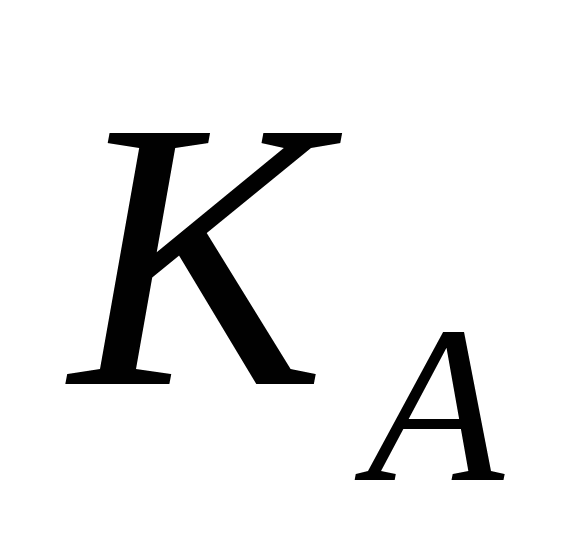 + +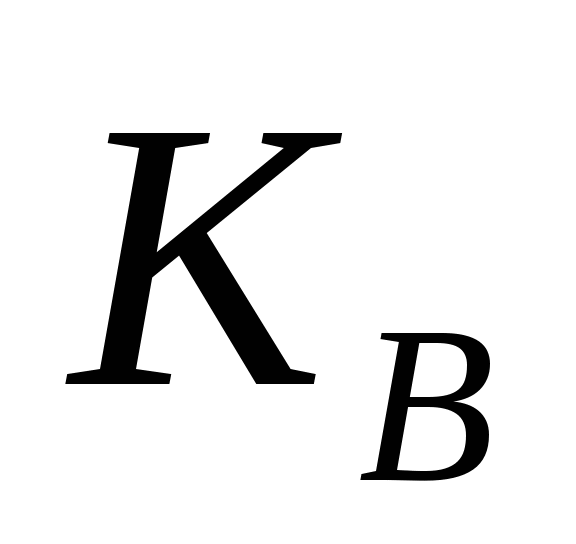 ,因此有 ,因此有 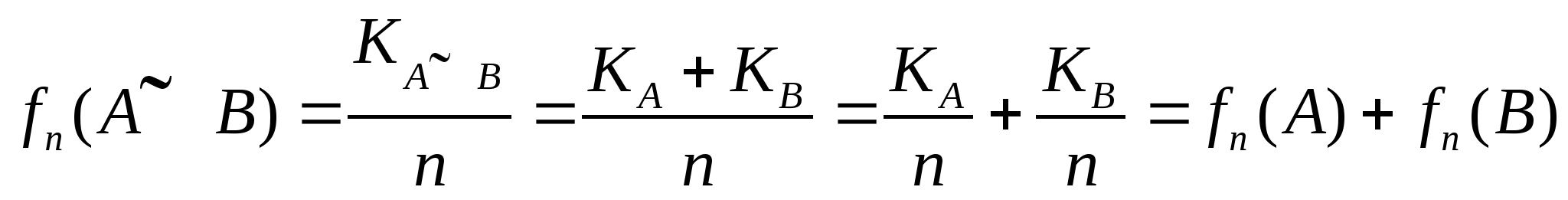
三、概率的统计定义 定义2 若事件 出现的频率随着试验次数 出现的频率随着试验次数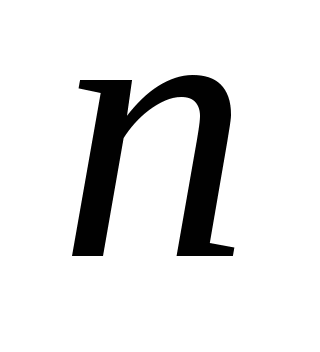 的增大而稳定于某一常数 的增大而稳定于某一常数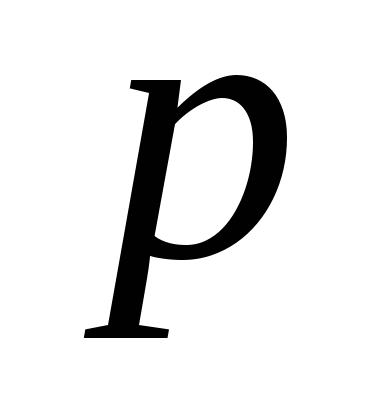 ,则称 ,则称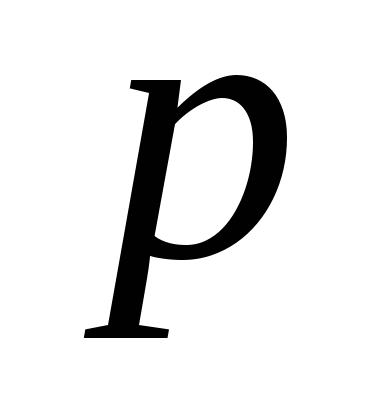 为事件 为事件 的概率.记作 的概率.记作 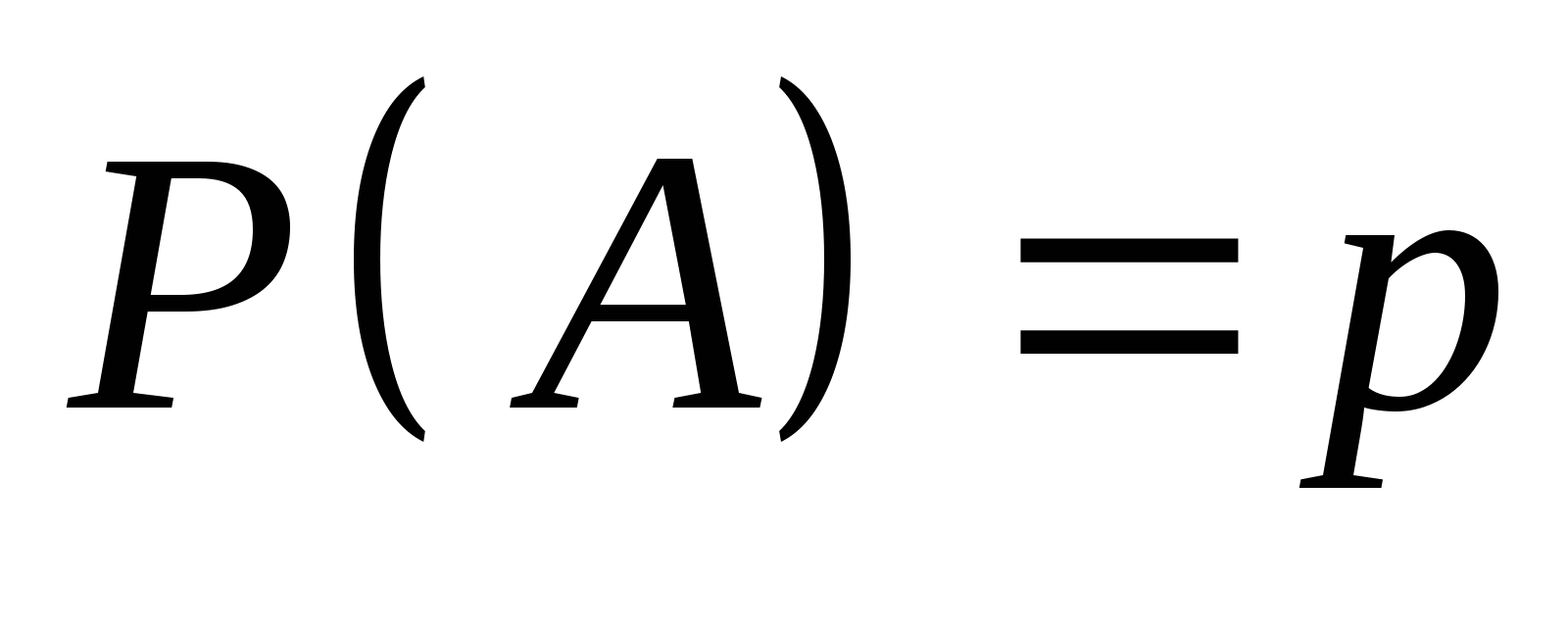 数值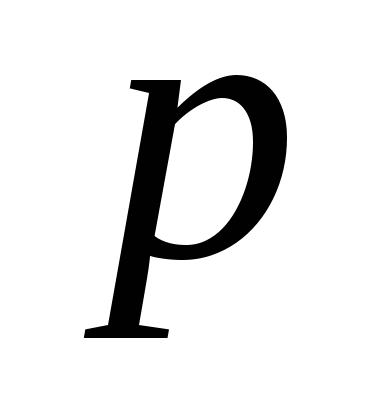 就是在一次试验中对事件 就是在一次试验中对事件 发生的可能性大小的数量刻划.例如,0.5就是刻画抛一枚硬币试验的事件 发生的可能性大小的数量刻划.例如,0.5就是刻画抛一枚硬币试验的事件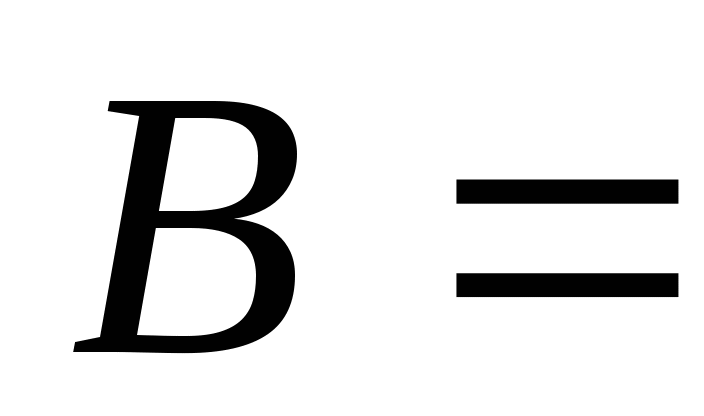 {正面向上 {正面向上 }的概率,即 }的概率,即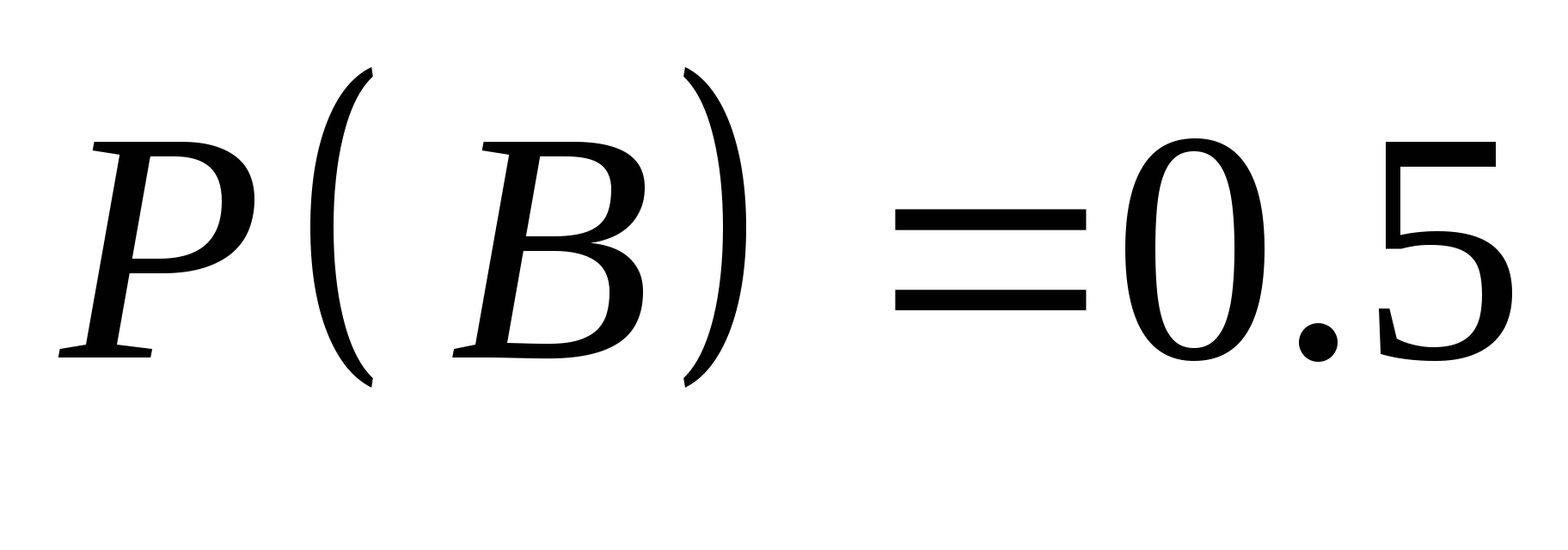 . . 由频率的性质和概率的统计定义即可得概率的如下性质 . . 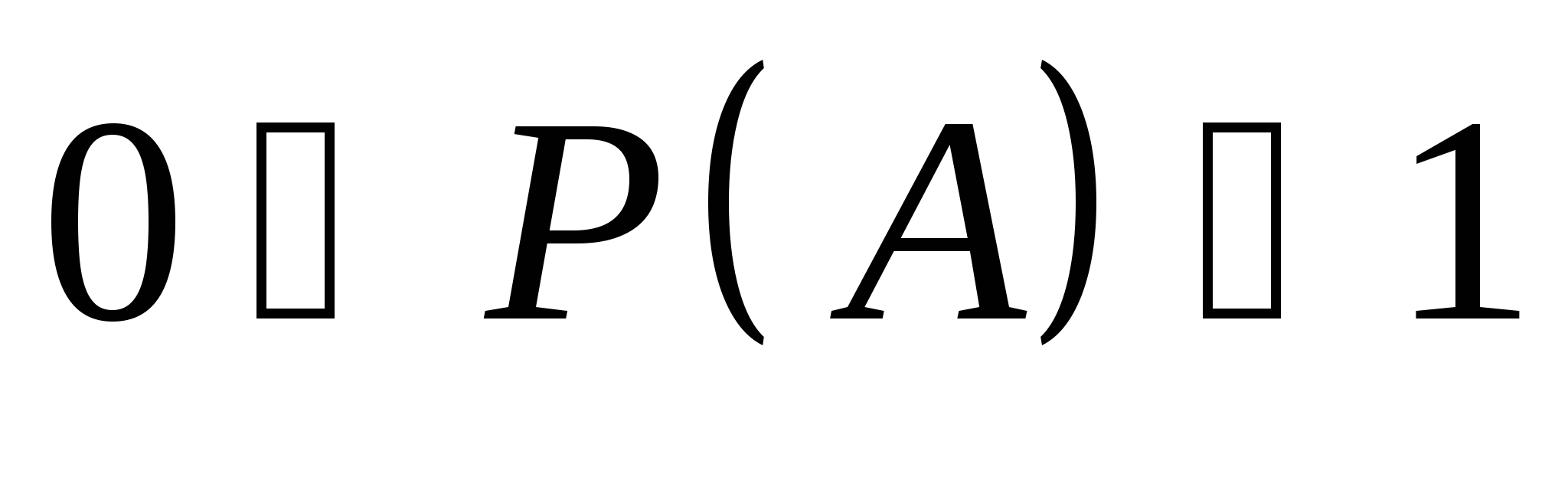 ; ; 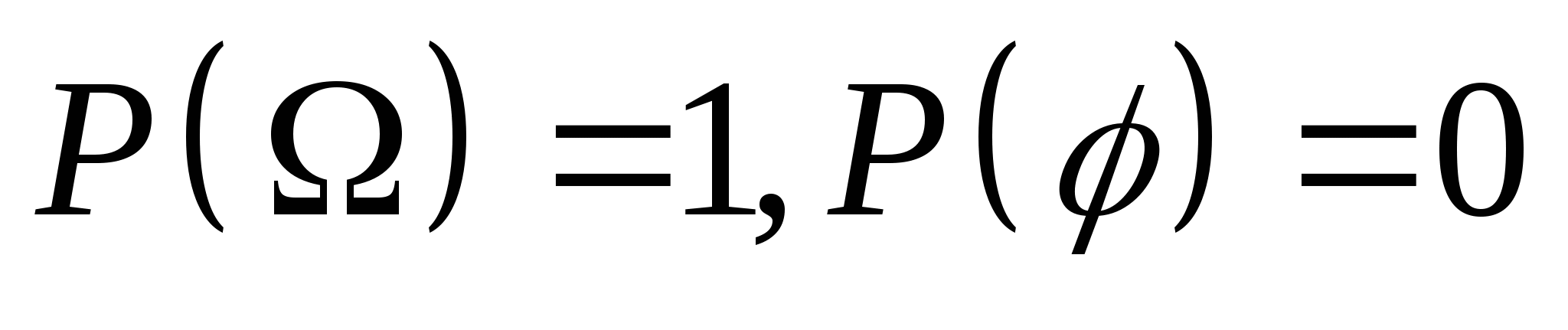 ; ;
对两两互斥的有限个随机事件 , , ,…, ,…,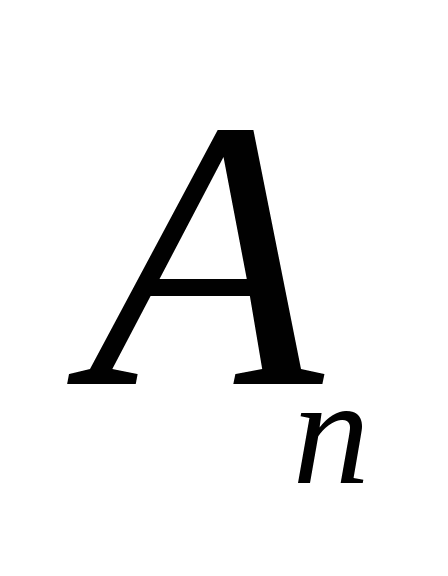 ,有 ,有
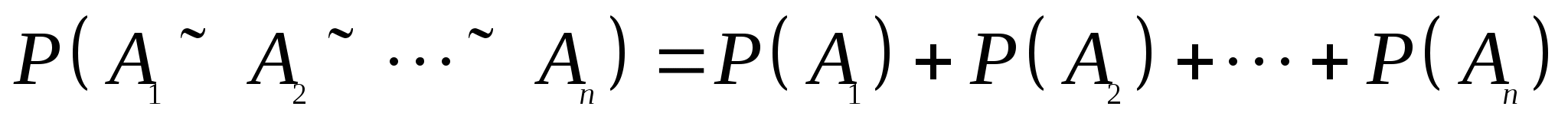 . .
性质(2)叫做概率的有限可加性.此性质可以推广至概率的可列可加性.即若事件 , , ,… ,…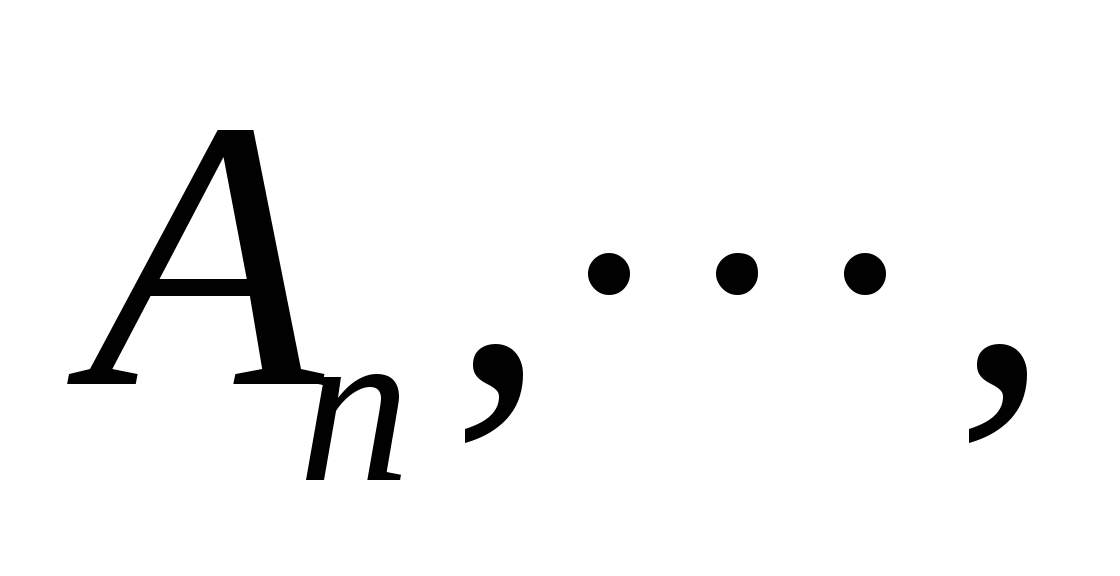 两两互斥,则 两两互斥,则 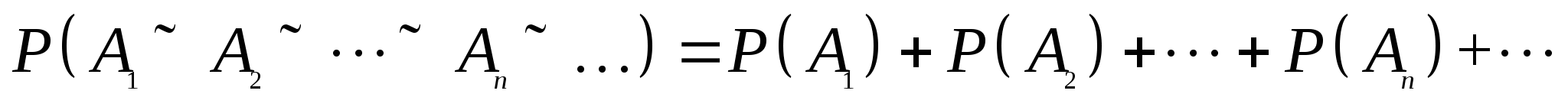
利用这些性质可以证明下面三个性质. 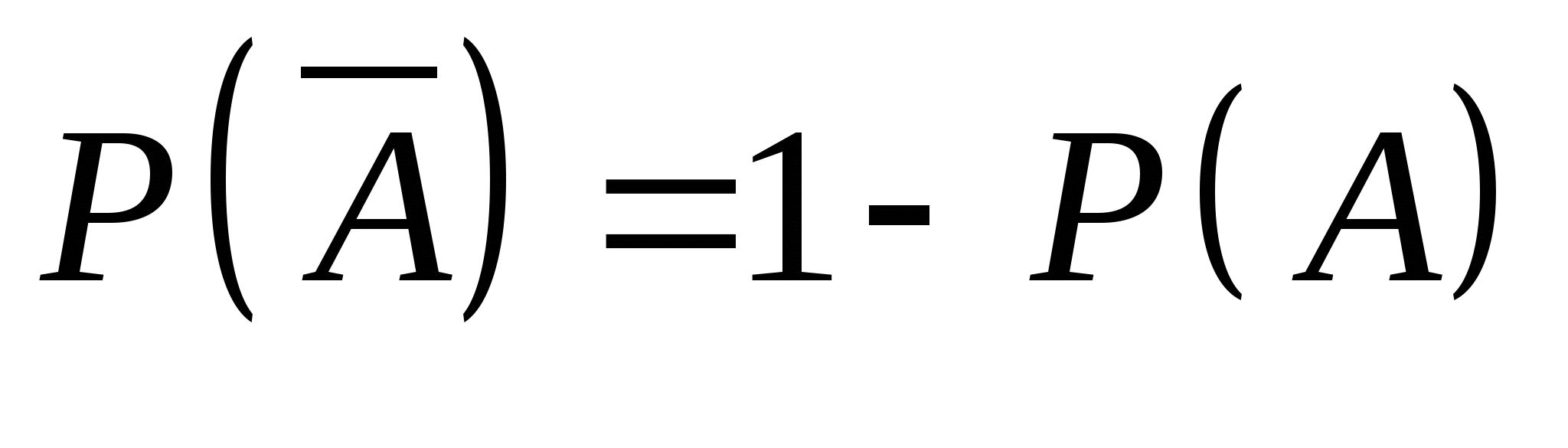 ; ;
若 ,则 ,则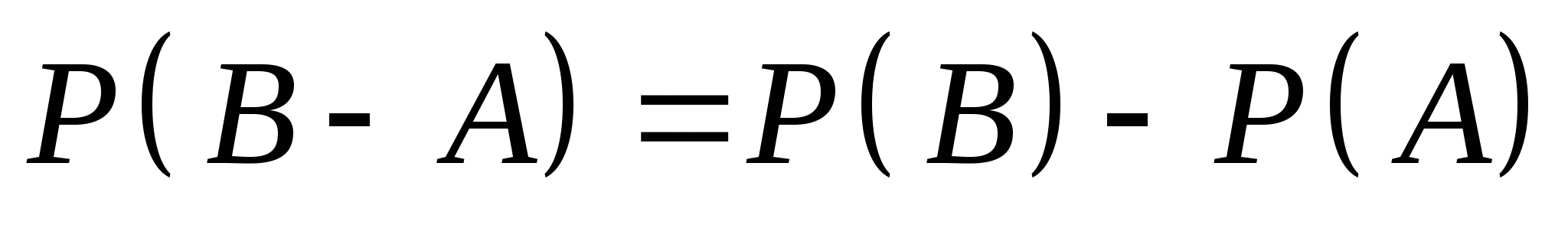 ; ;
若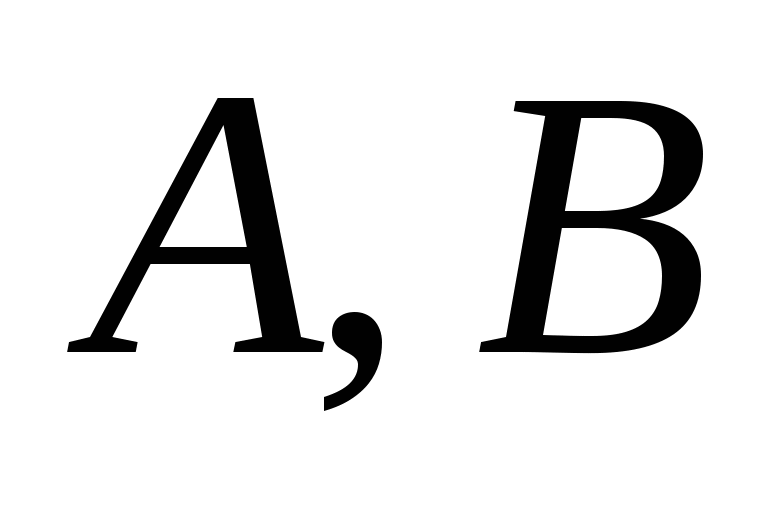 为任意事件,则 为任意事件,则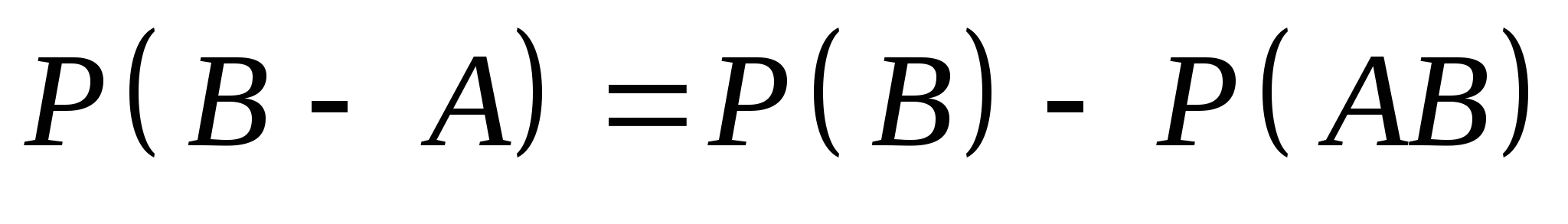 ; ; (6)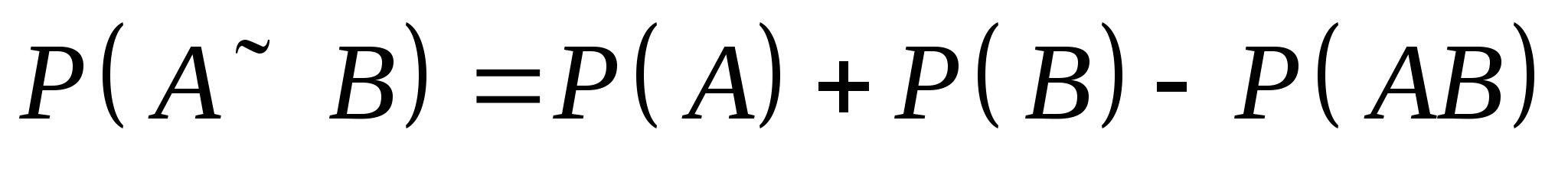 . . 性质(6)叫做概率加法公式,性质(3)是它的特例. 例1 设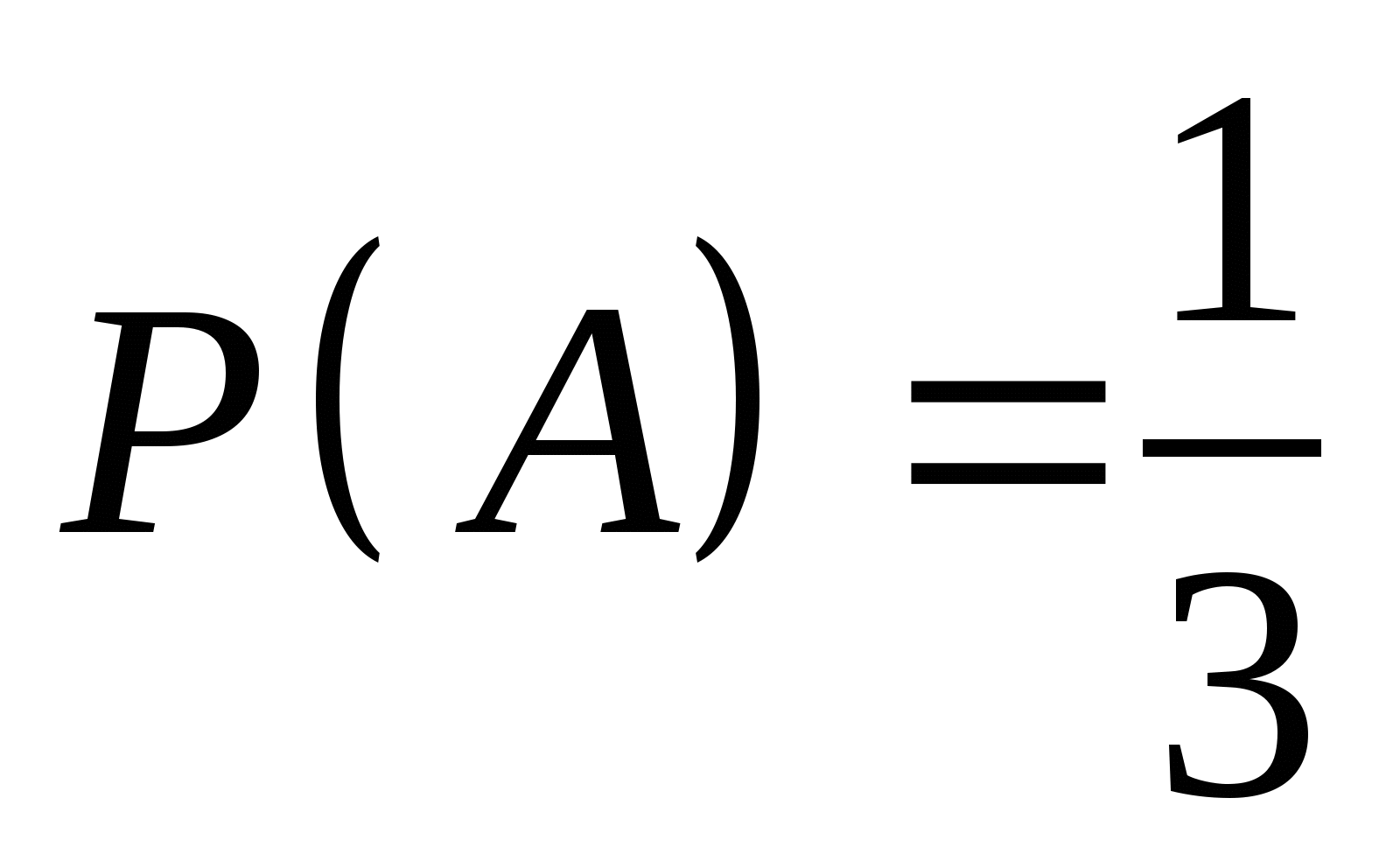 , ,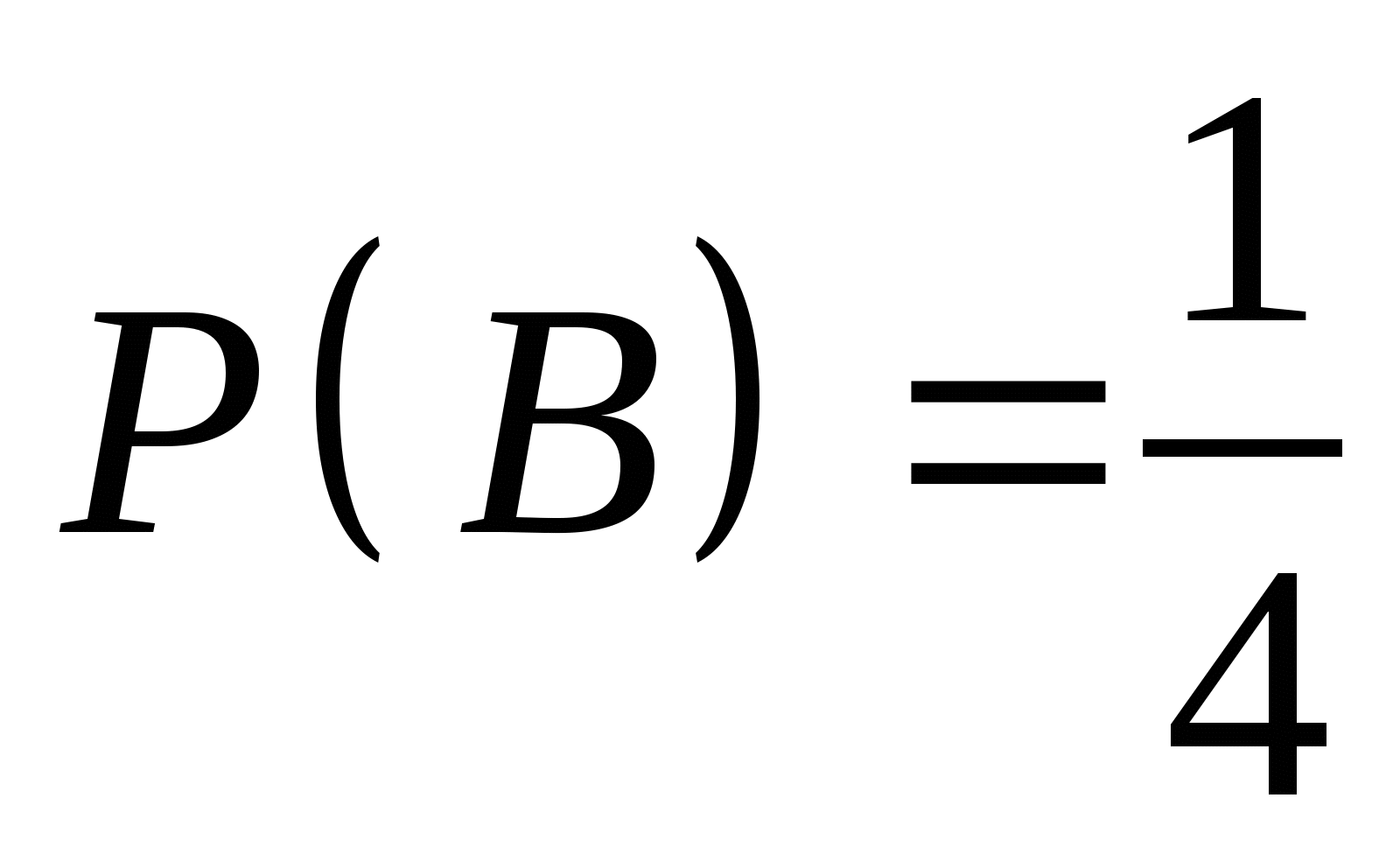 ,在下列三种情况下,求 ,在下列三种情况下,求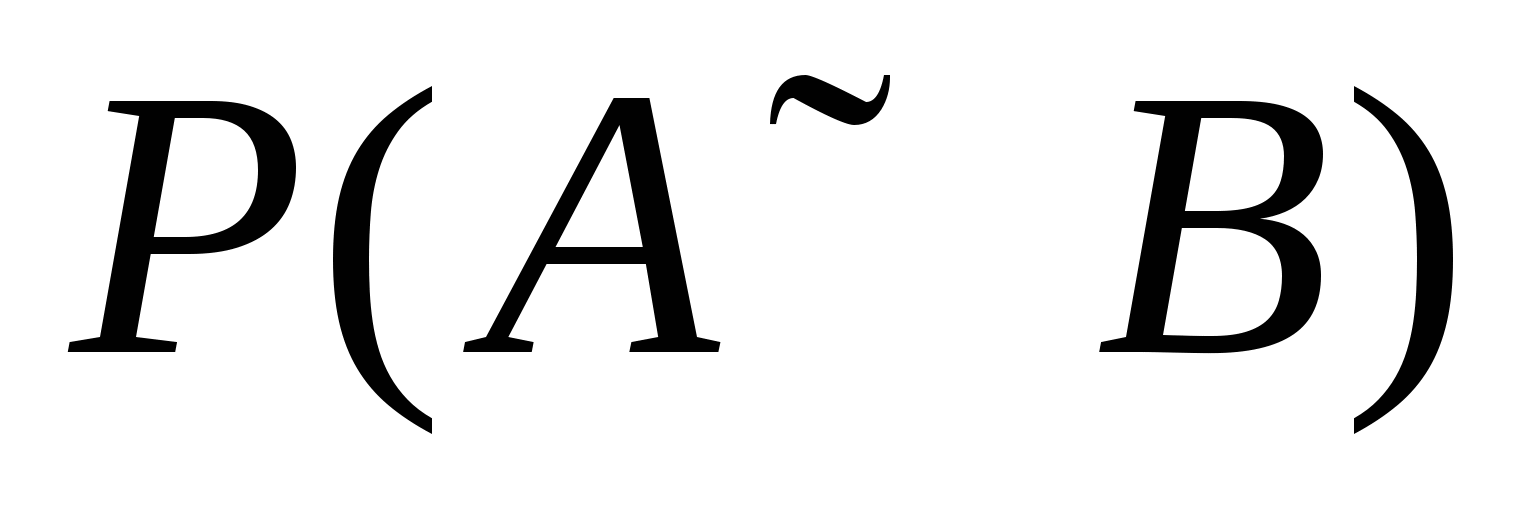 及 及 的值. 的值. (1) 与 与 互斥; (2) 互斥; (2) ; (3) ; (3)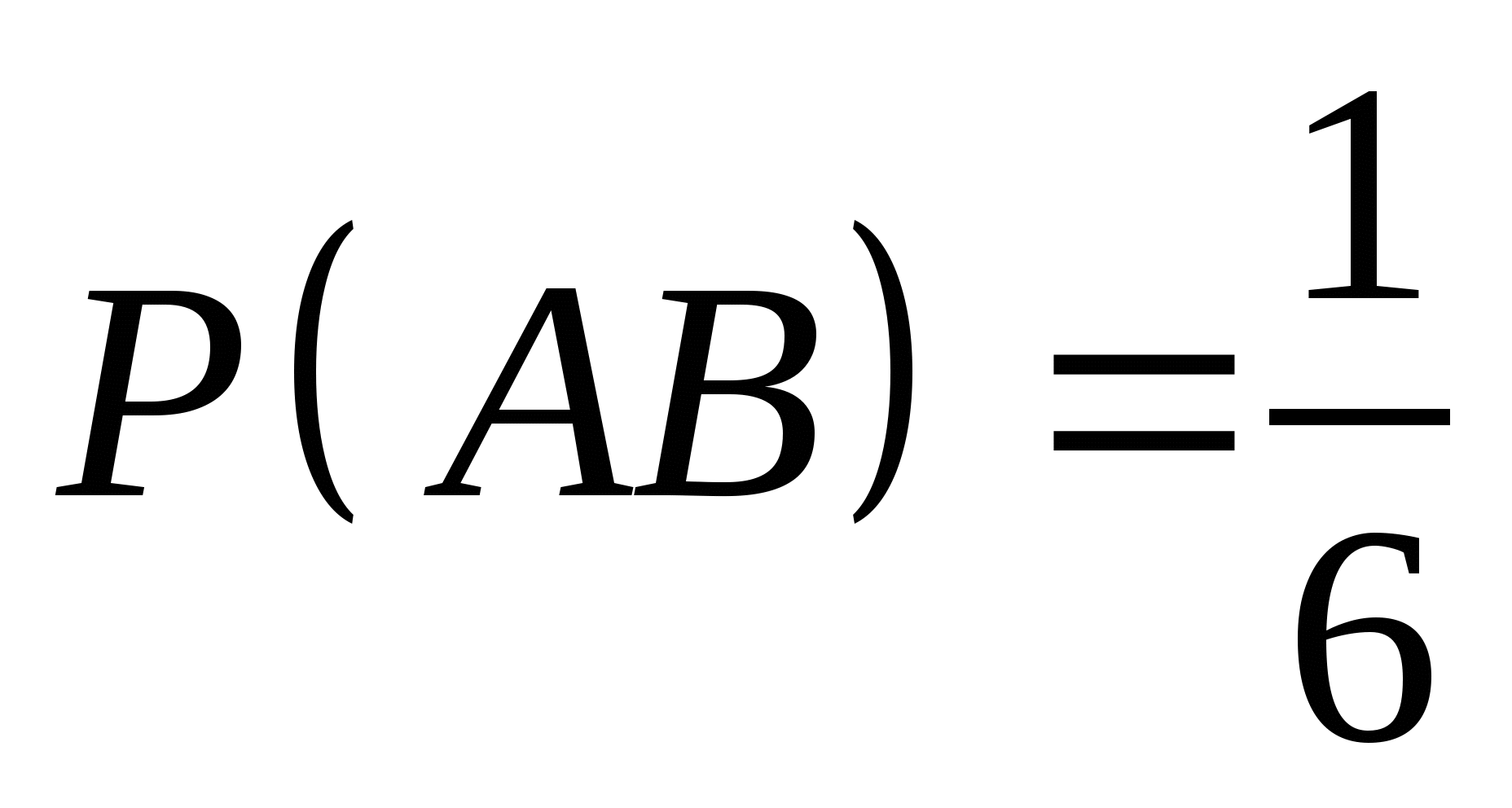 . . 三、古典概型 1. 古典概型 如果一个试验E具有以下两个特点: (1)样本空间 是由有限个样本点组成的,即其基本事件的个数是有限的; 是由有限个样本点组成的,即其基本事件的个数是有限的; (2)每个基本事件出现的可能性相同(也叫做等可能性). 则称E为古典型随机试验,相应的数学模型叫做古典概型.古典概型在实践中有广泛的应用,它在概率论中占有相当重要的地位.对于古典概型,设其样本空间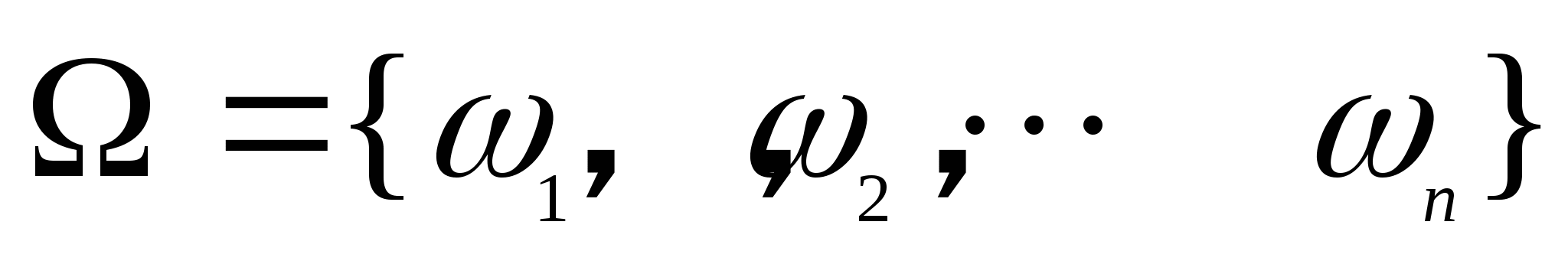 ,由于 ,由于 ,且诸 ,且诸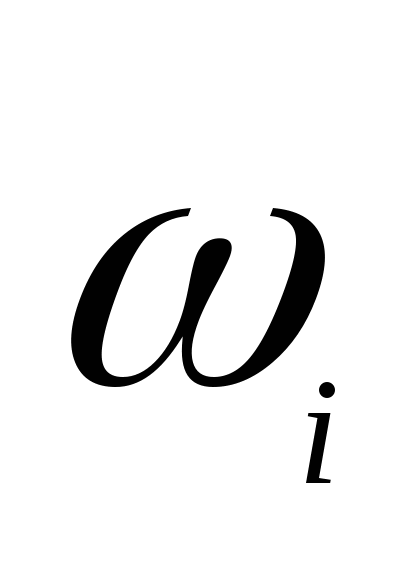 间是互不相容的,利 间是互不相容的,利 2 概率的古典定义 定义3 对于古典概型,设其样本空间包含基本事件的个数为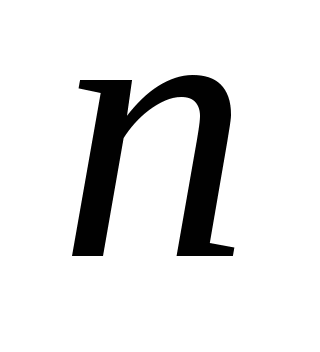 ,事件 ,事件 包含基本事件的个数为 包含基本事件的个数为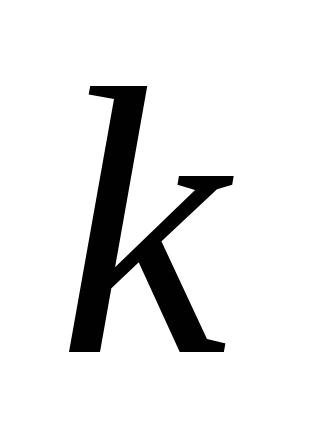 ,则称比值 ,则称比值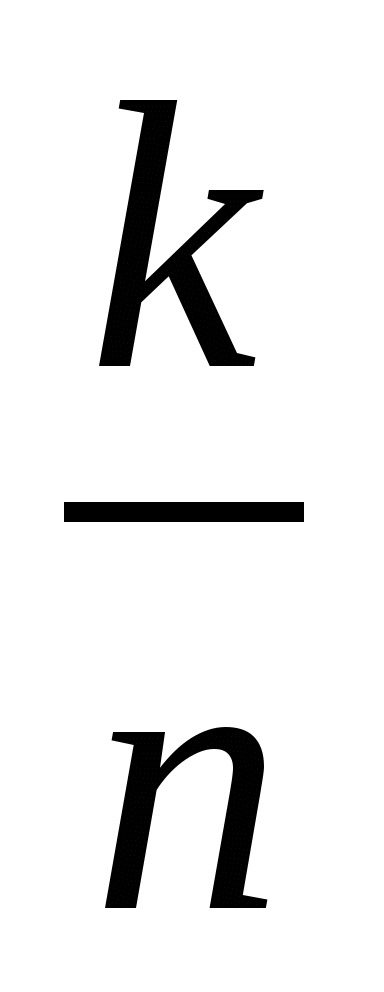 为事件 为事件 的概率,记作 的概率,记作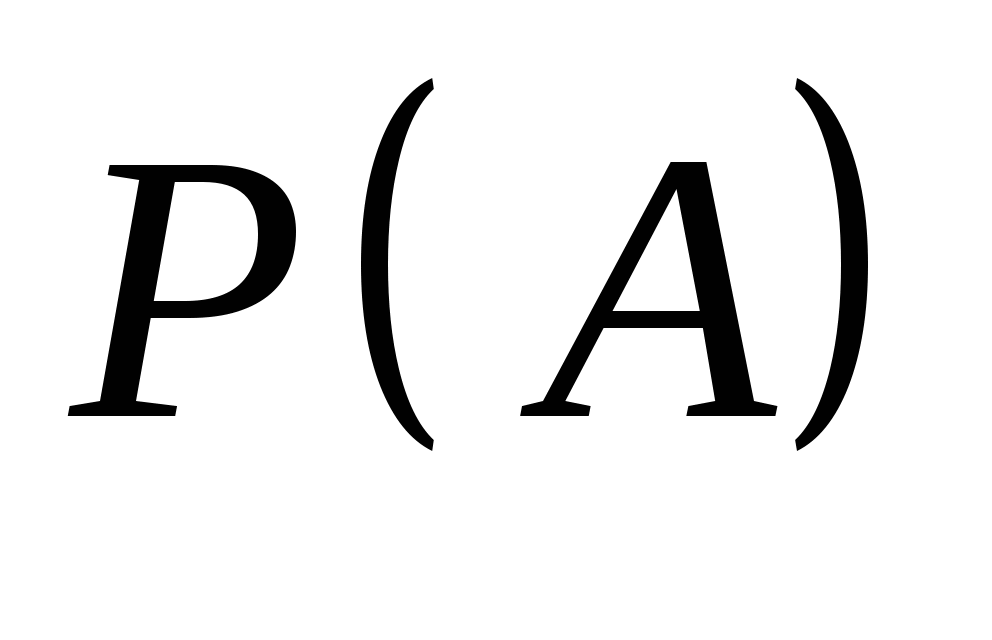 即 即 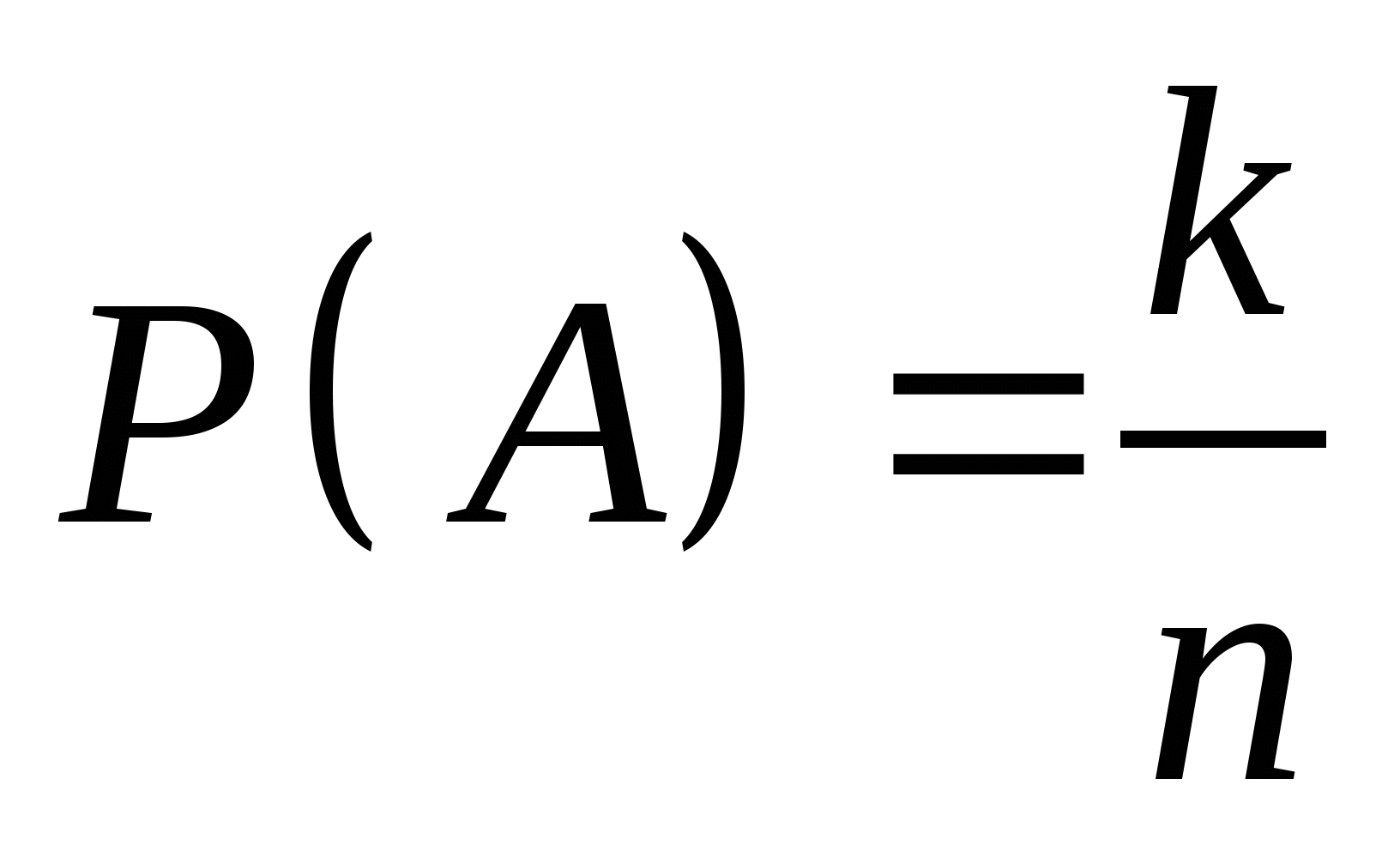
此定义叫做概率的古典定义. 例2 10件产品中,有8件正品,2件次品,任取一件产品,求取得次品的概率. 例4 一罐中装有4个白球,3个黑球,从这7个球中一次任取3个球,问它们全是白球的概率是多少? 例5 设 件产品中,有 件产品中,有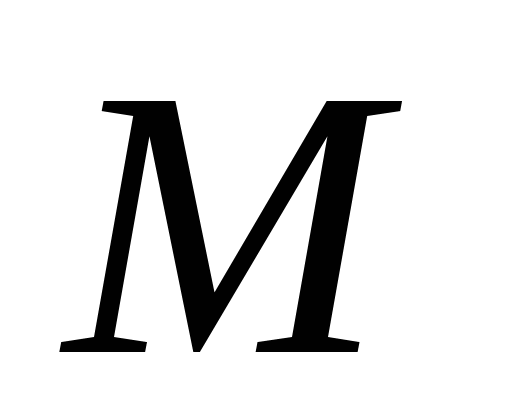 件次品.从 件次品.从 件中任取 件中任取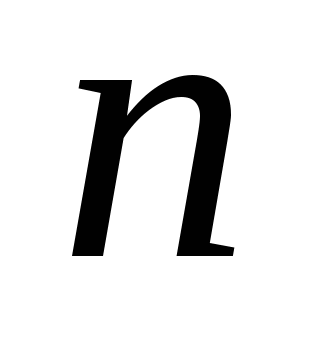 件( 件(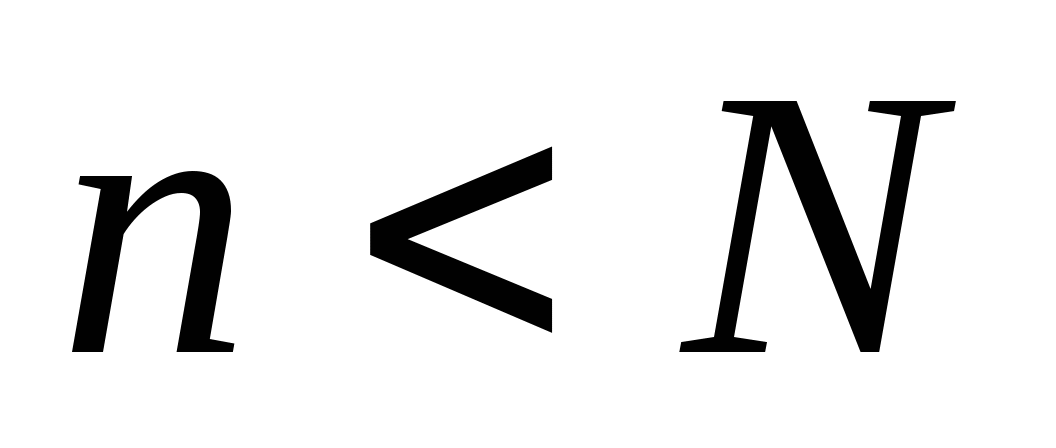 ).求 ).求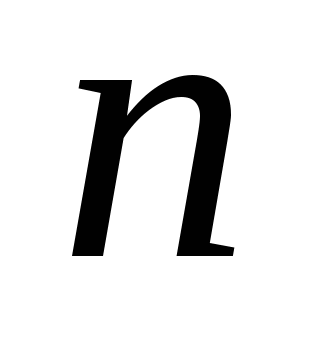 件中恰有 件中恰有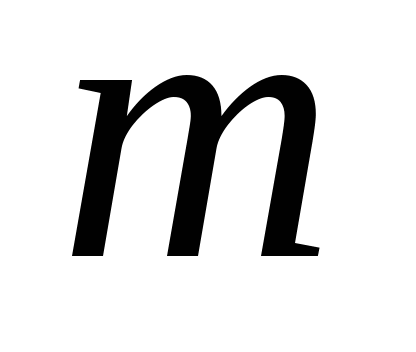 件次品的概率( 件次品的概率(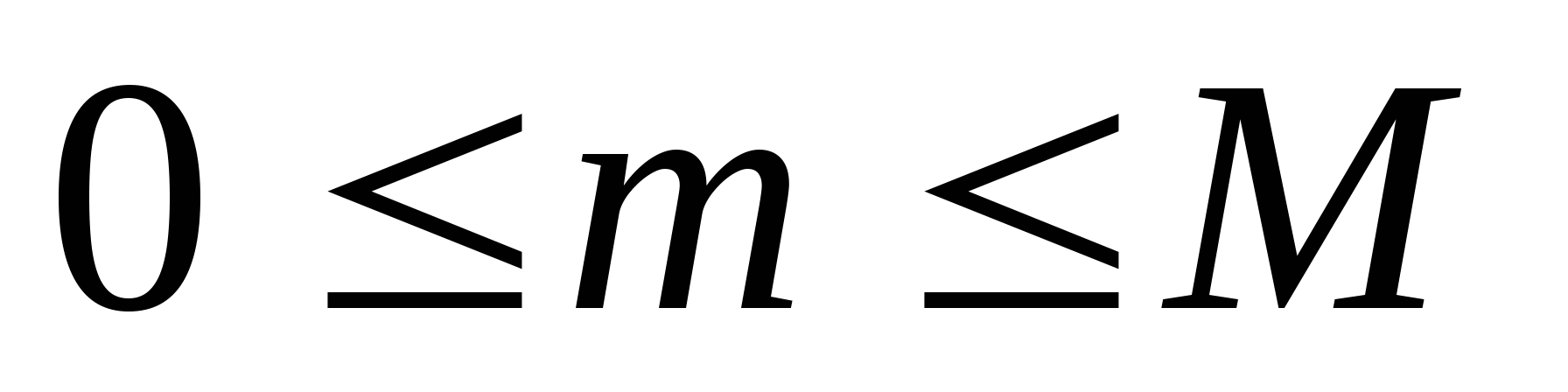 ). ). 例6 一口袋中装有红、白、黄色球各一个.从中随机抽取三次,每次取一个球,取后观察其颜色后放回.再取下一个球,求三次都取白球的概率. 需要注意的是:
1、在应用古典概型时必须注意“等可能性”的条件.; 等可能性”是一种假设,在实际应用中,我们需要根据实际情况去判断是否可以认为各基本事件或样本点是等可能的.
2、在用排列组合公式计算古典概率时,必须注意不要重复计数,也不要遗漏. 3、许多表面上提法不同的问题实质上属于同一类型:
小结:介绍了古典概型及概率的古典定义,着重举例说明如何进行古典概率的计算. 第三节 条件概率及乘法公式 一、条件概率 定义1 设 , ,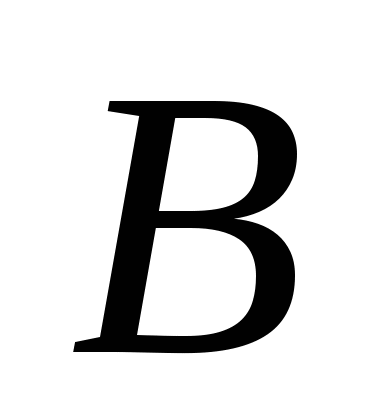 是两个事件,且 是两个事件,且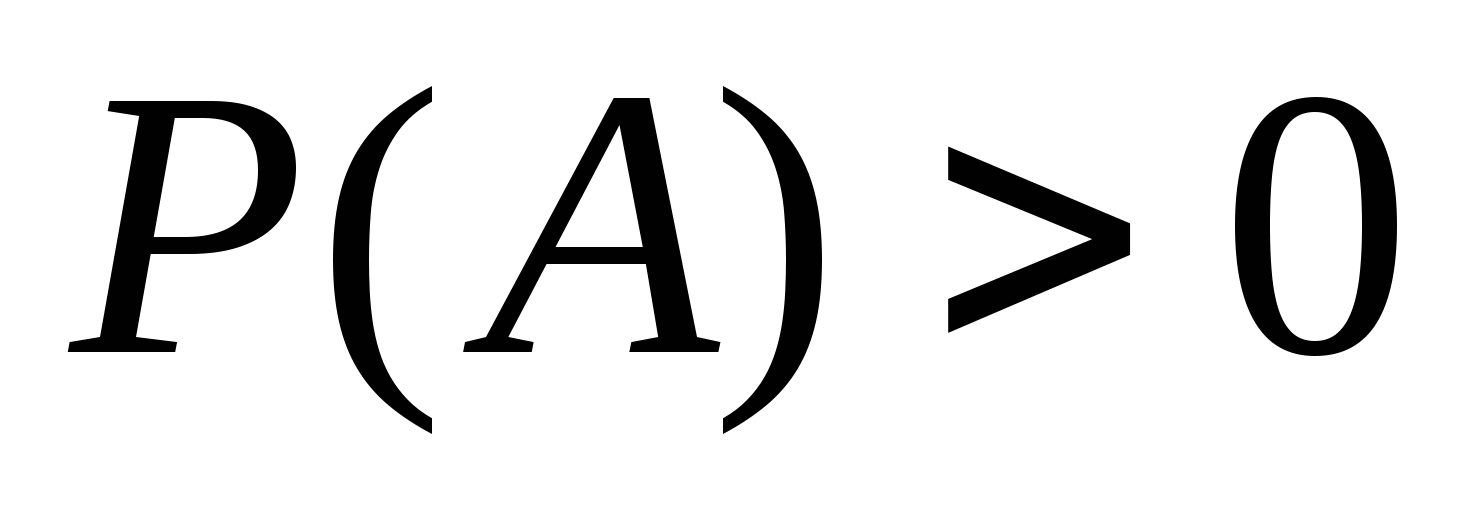 ,则 ,则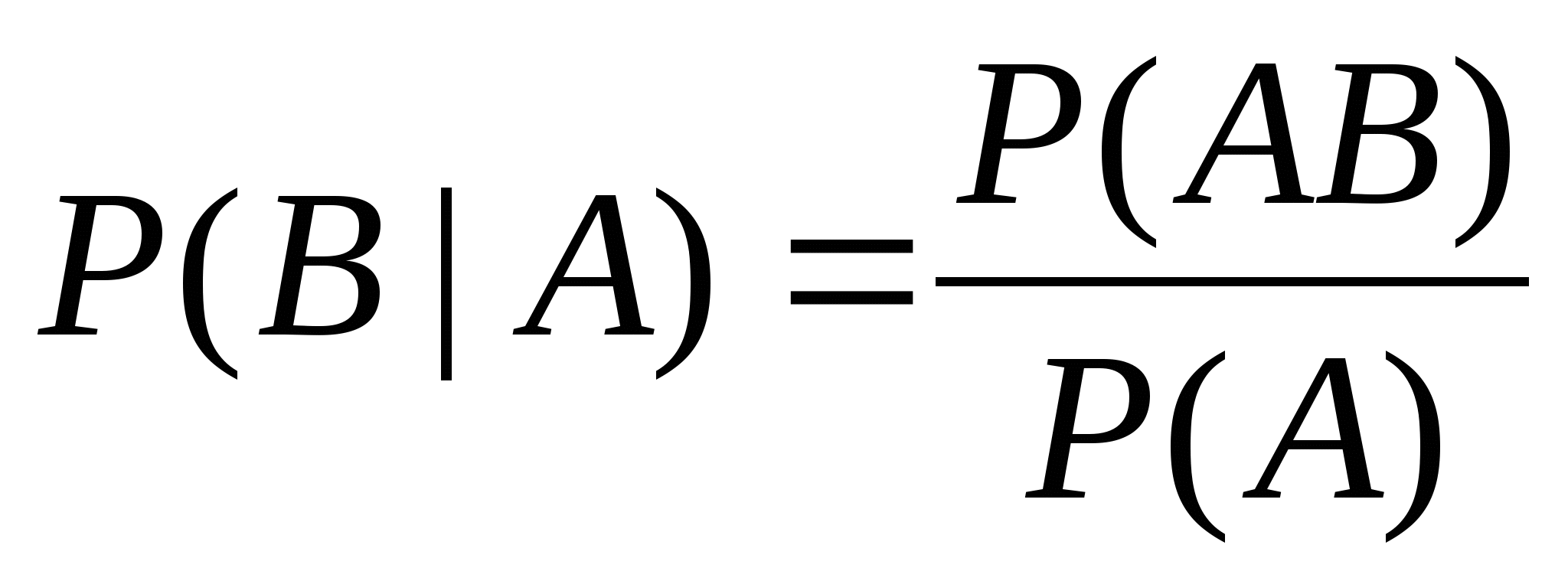 (1) (1) 为在事件 发生的条件下,事件 发生的条件下,事件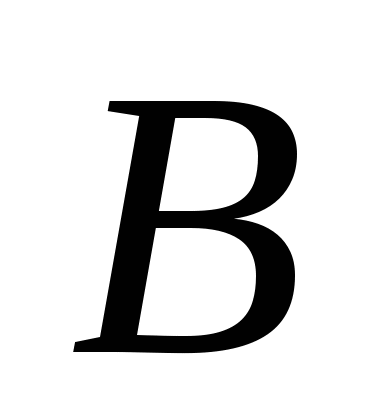 发生的条件概率;称 发生的条件概率;称 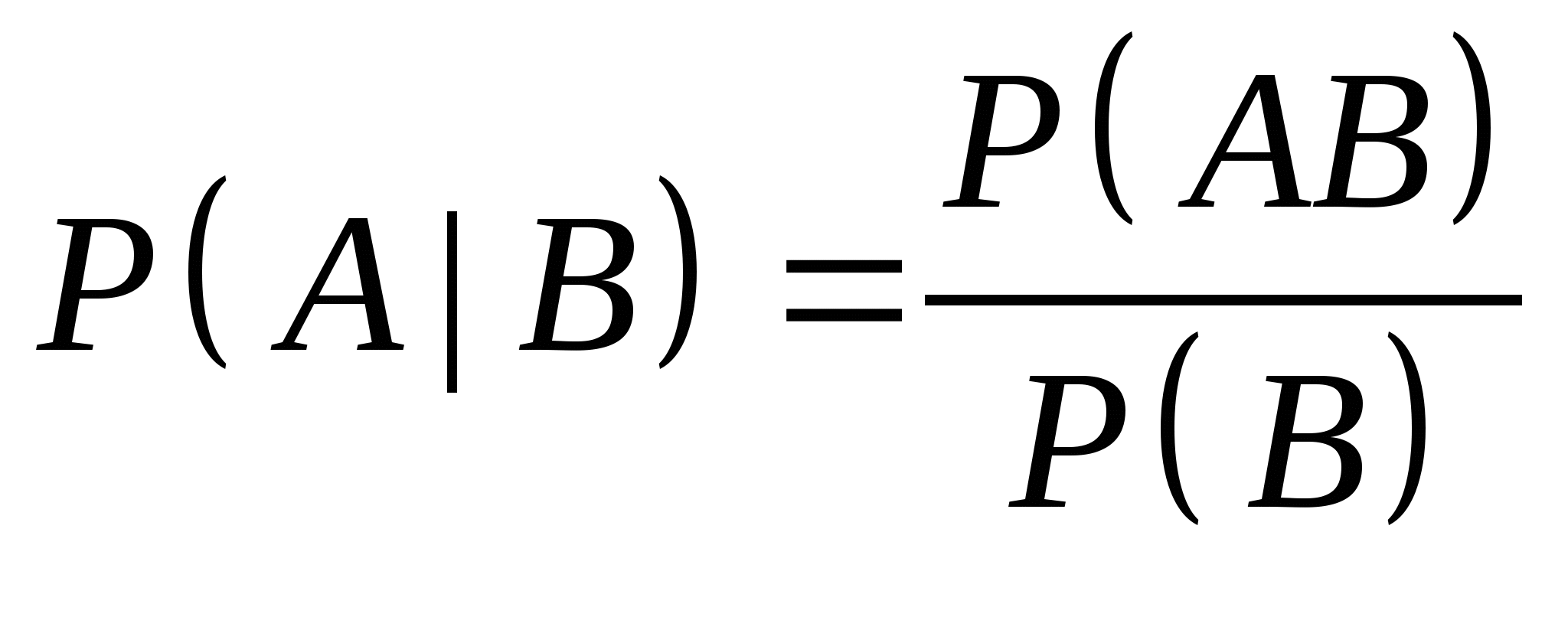 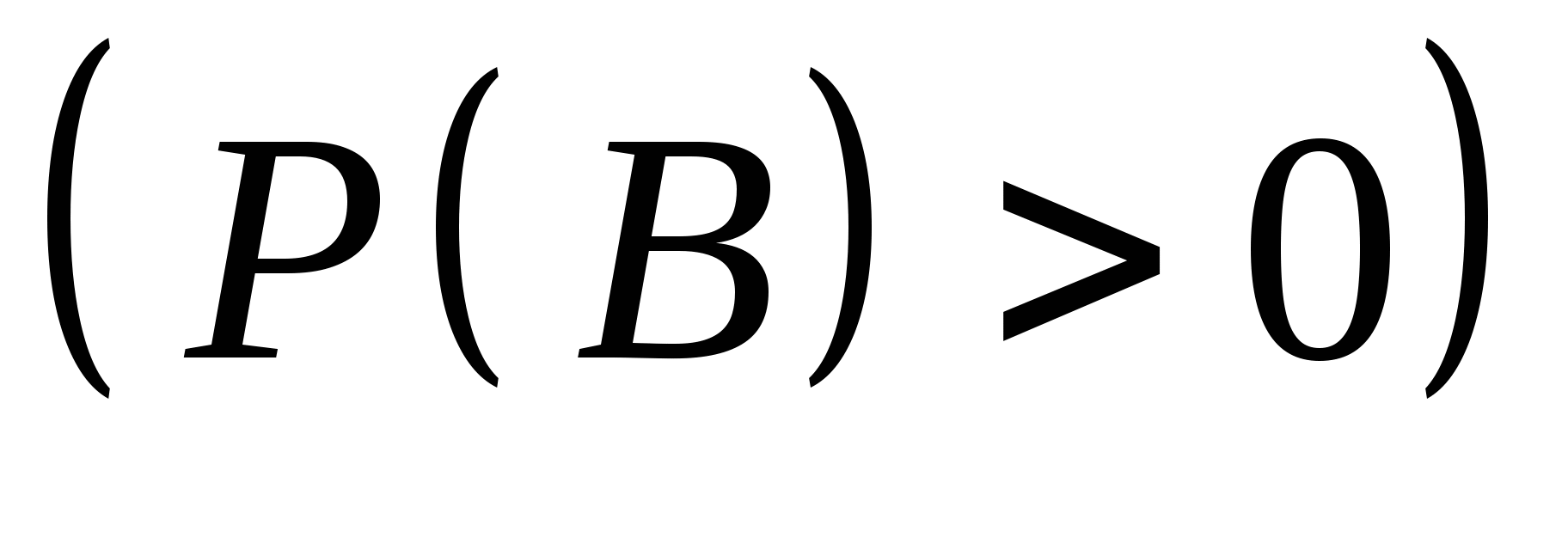 (2) (2)
为在事件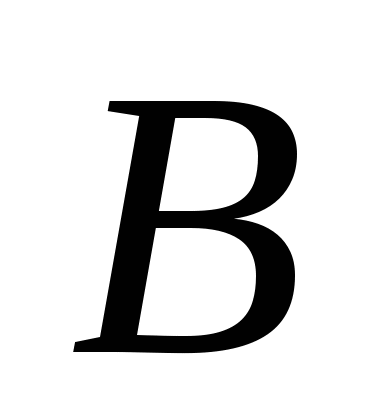 发生的条件下,事件 发生的条件下,事件 发生的条件概率. 发生的条件概率.
不难验证上一节给出的概率性质,对条件概率仍然成立,即有 (1)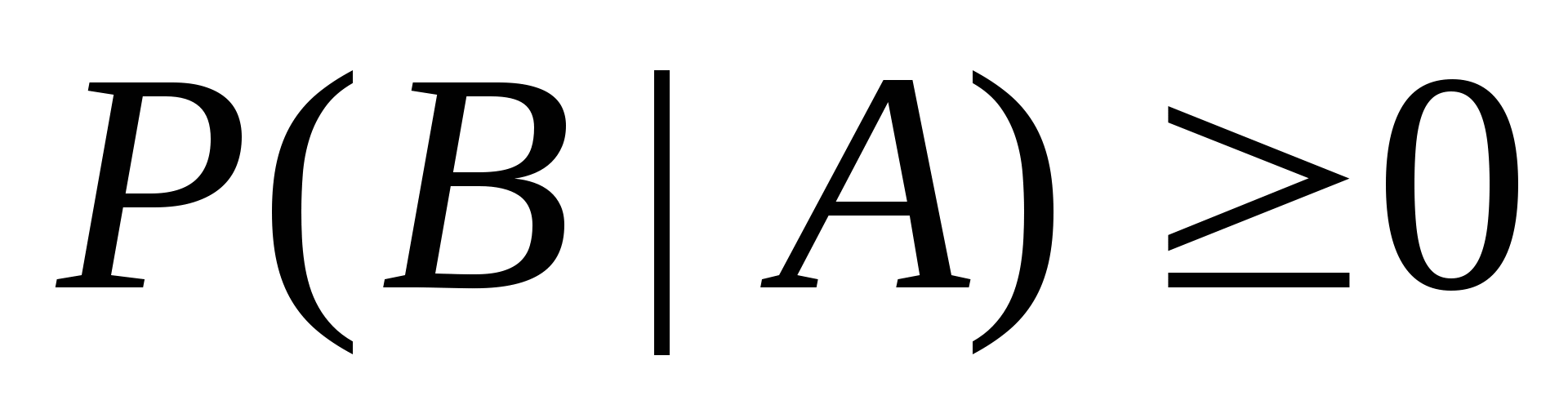 ; (2) ; (2)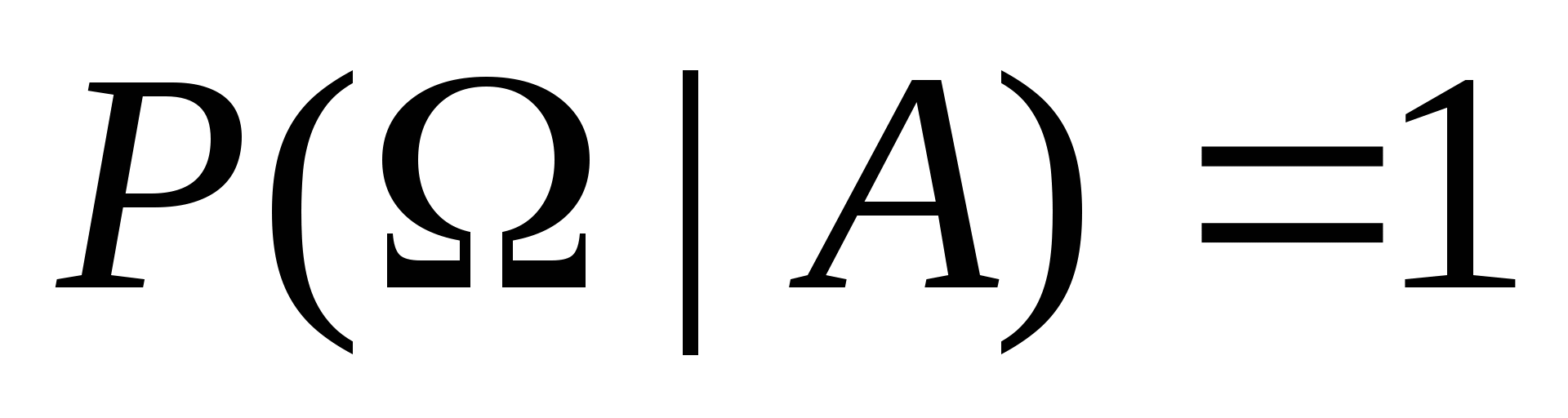 ; ; (3)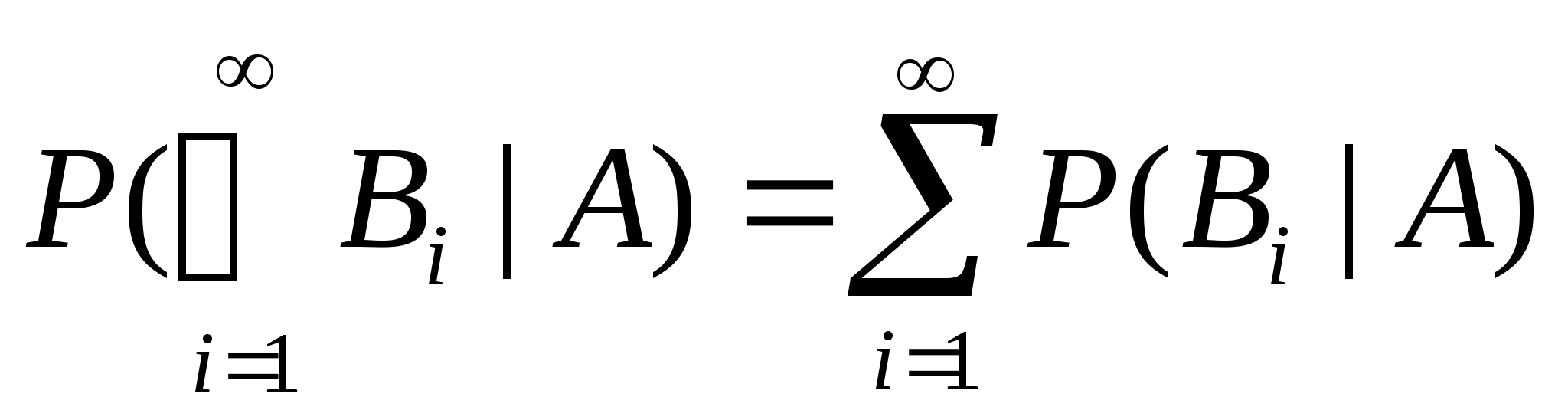 ,(其中 ,(其中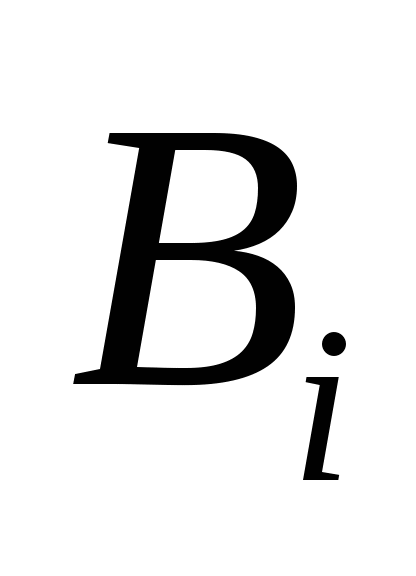 两两互斥); (4) 两两互斥); (4)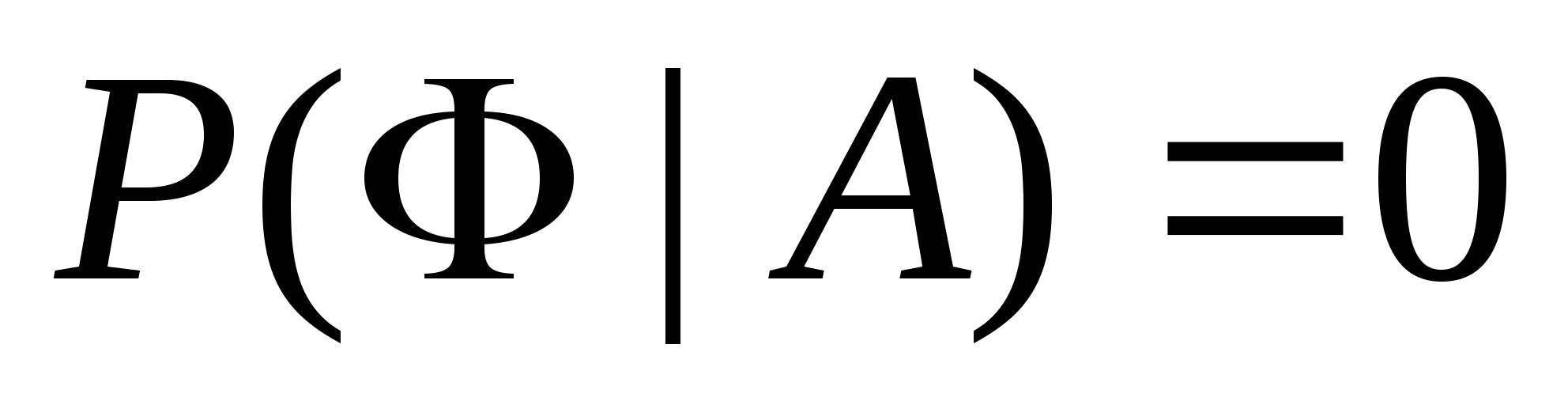 ; ; (5)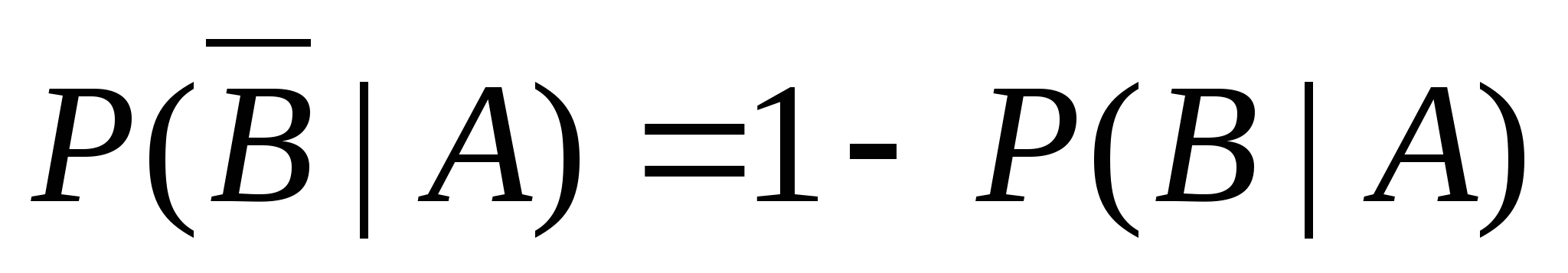 . . 例1 甲、乙二车间生产同一种产品共1500个,已知甲车间生产600个产品中正品数为560个.现从1500个中任取一个,已知它是甲车间生产的,求取到正品的概率. 二、概率的乘法公式 由公式(1)及(2)即得 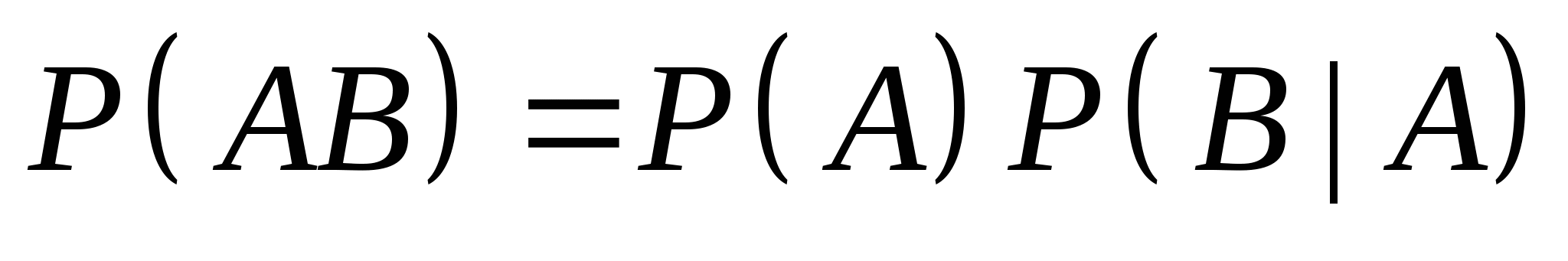 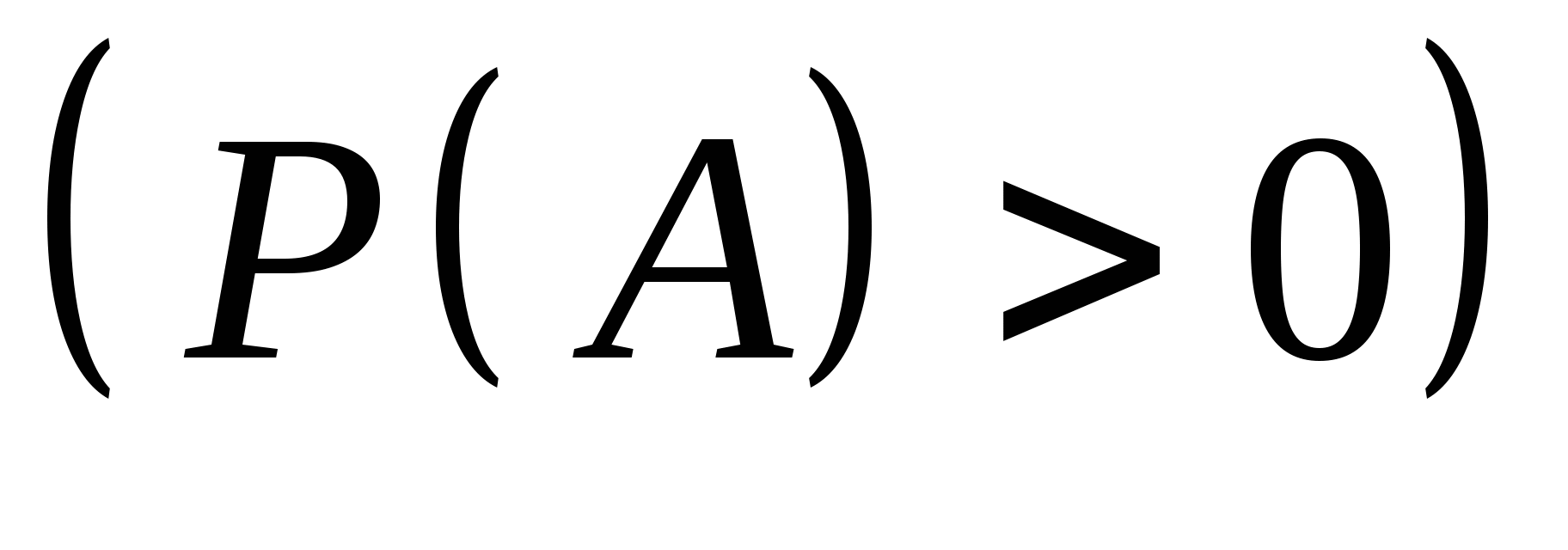
=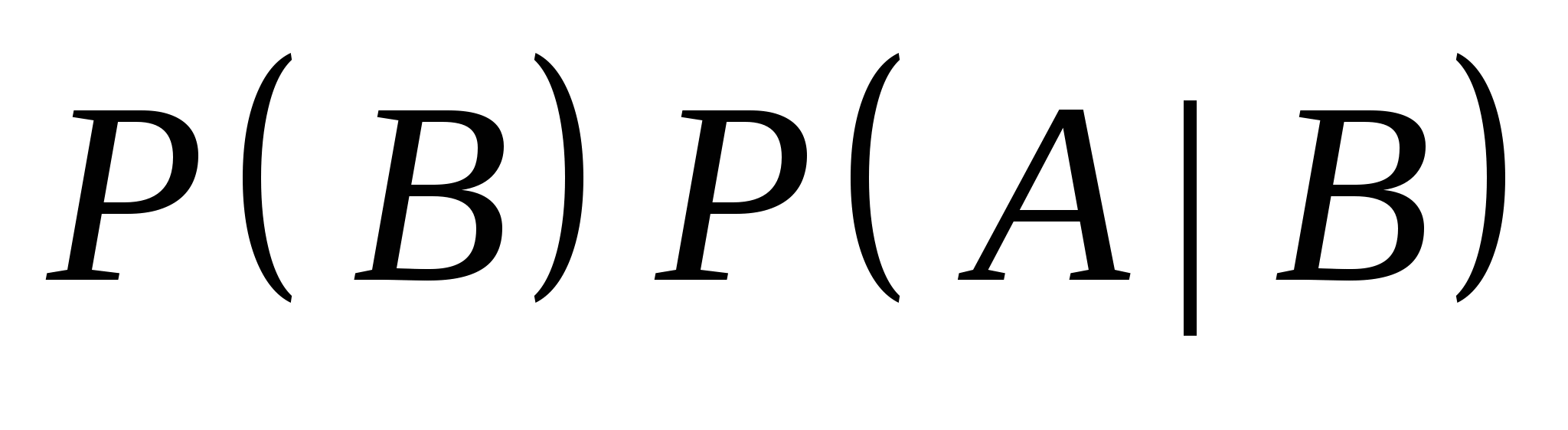 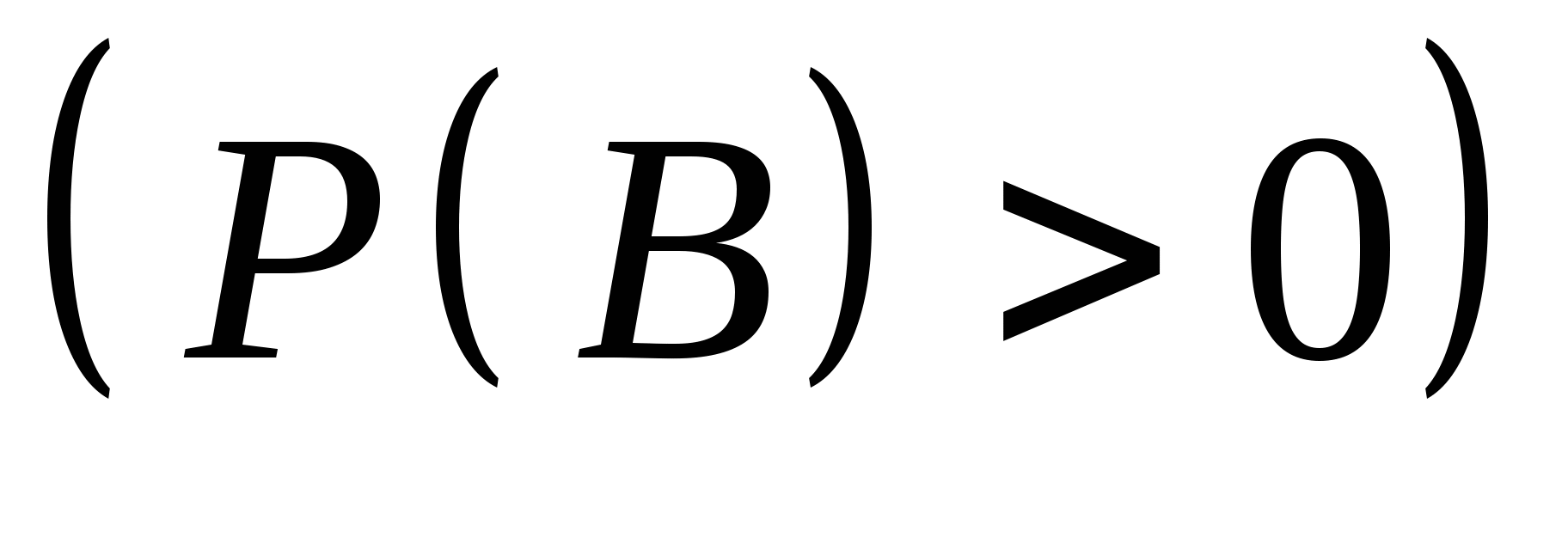 (3) (3) 公式(3)叫做概率的乘法公式. 例2 在10个球中有4个新球,现有甲乙2人取球(不放回),按甲、乙的次序,每人取一球.求(1)甲、乙都取到新球;(2)甲没有取到新球而乙取到新球的概率. 概率的乘法公式(3)可以推广到多个事件的情形.一般地,对事件 , , ,…, ,…,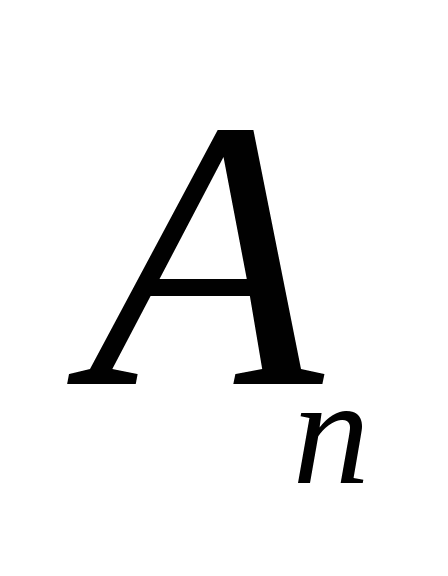 ,若 ,若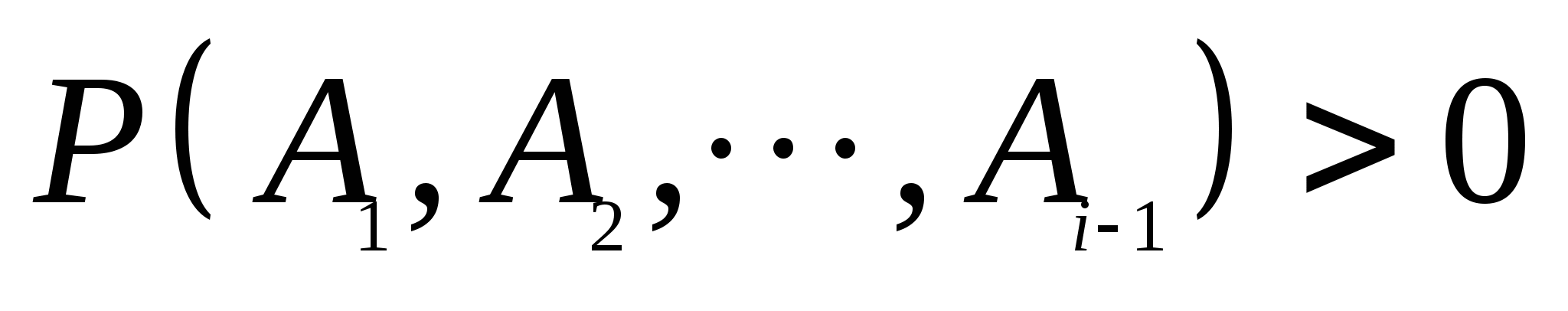 则有 则有 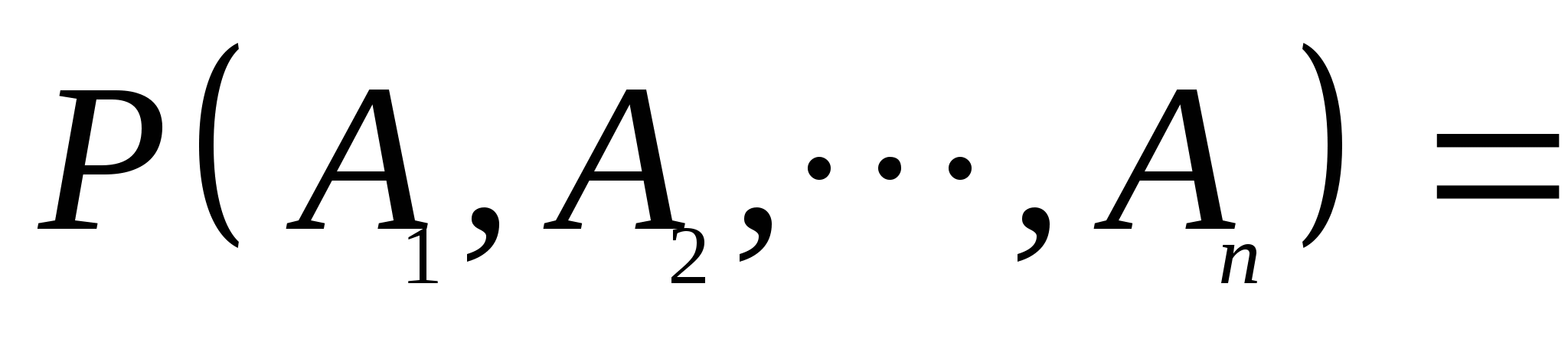 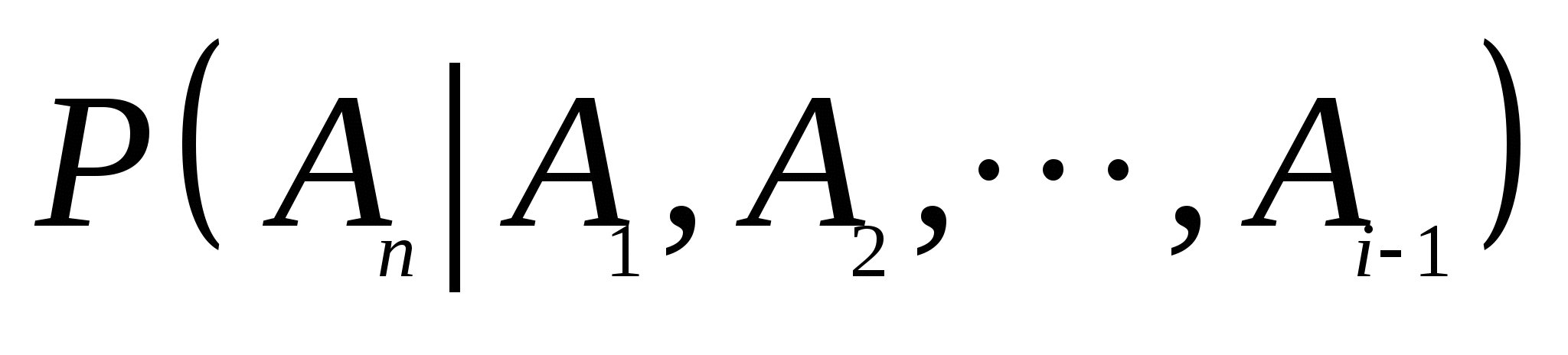 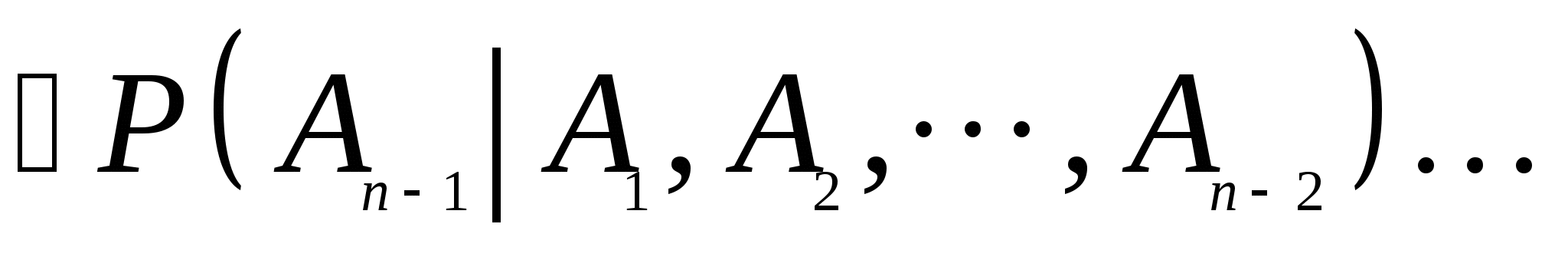
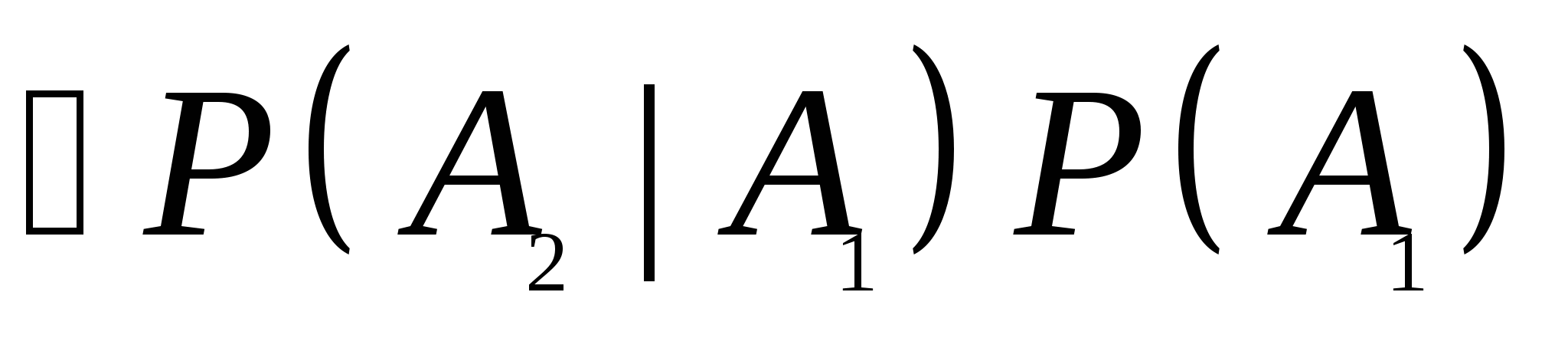
二、全概率公式 设事件 , , ,…, ,…,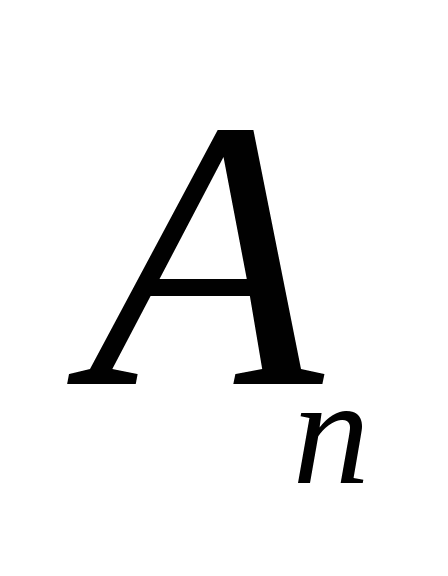 两两互斥, 两两互斥,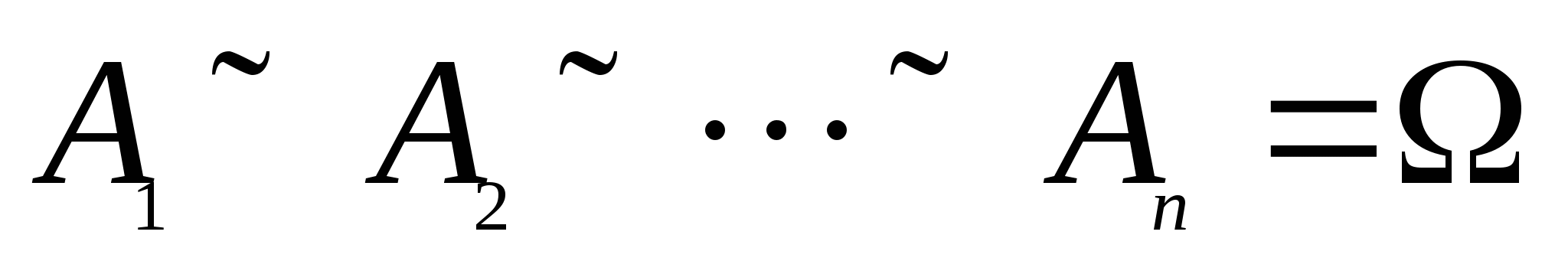 ,且 ,且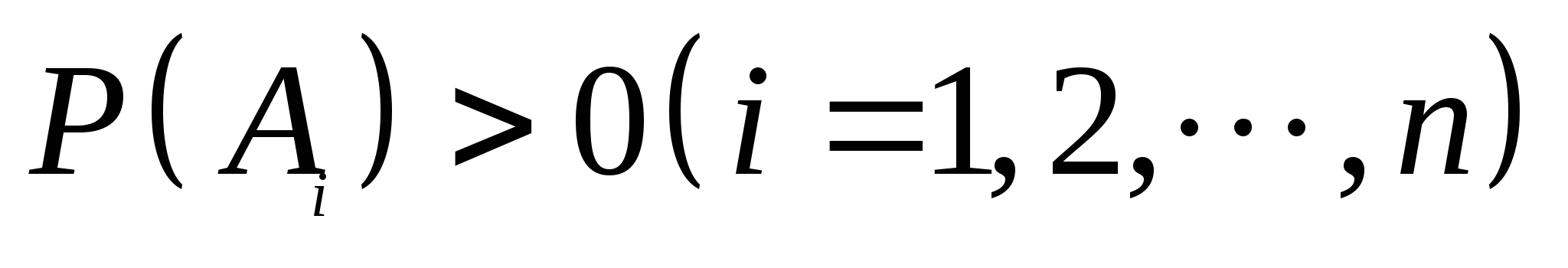 , , 为任一事件,则 为任一事件,则 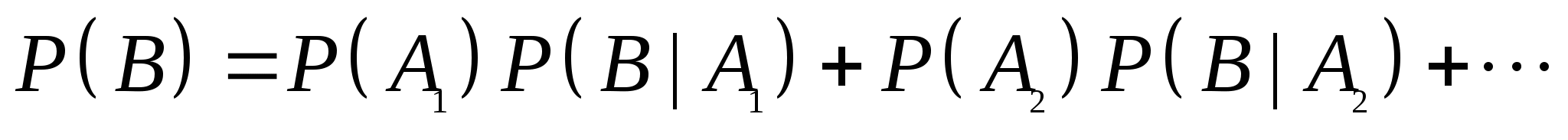 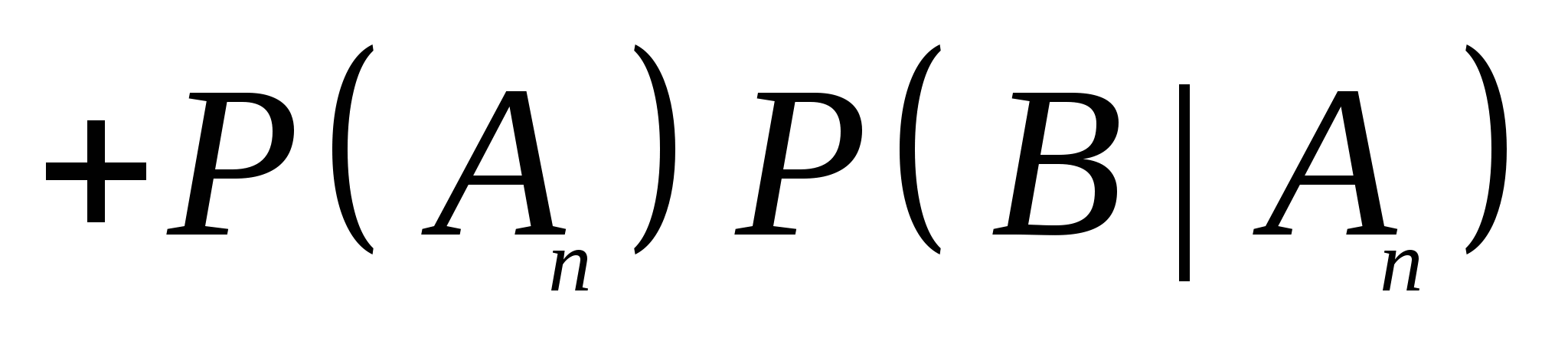 (5) (5)
=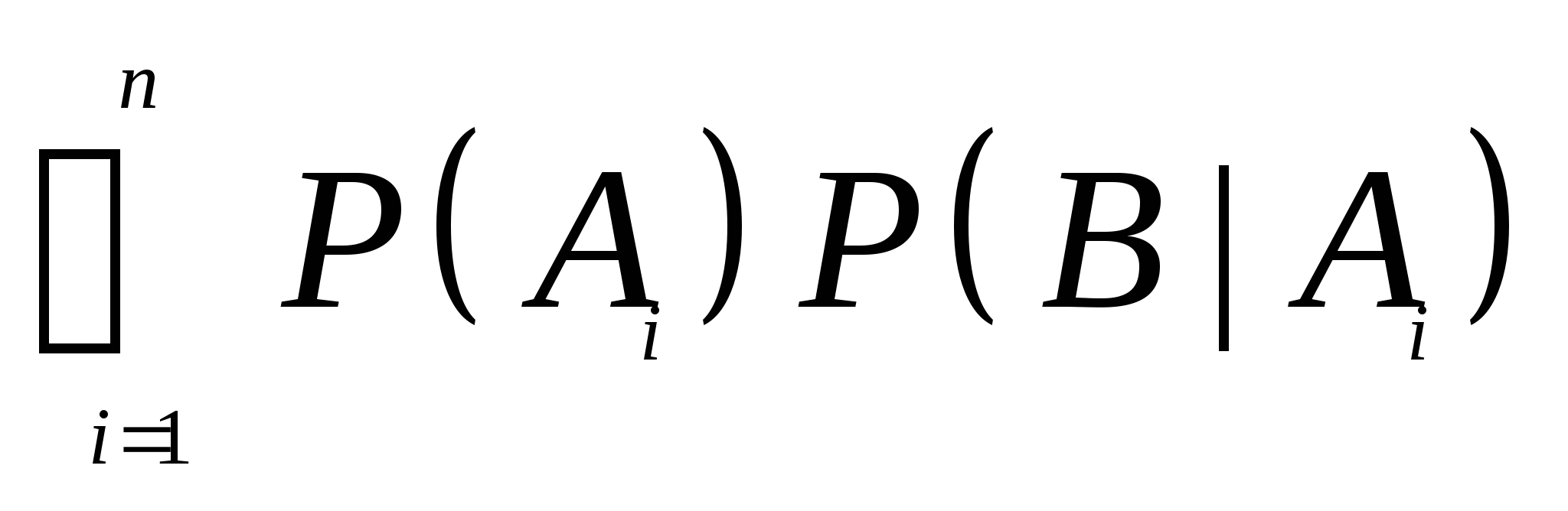 (5)式叫做全概率公式. 例4 一仓库中有甲、乙、丙厂生产的同样型号的产品,已知其中甲、乙、丙厂生产的分别是总量的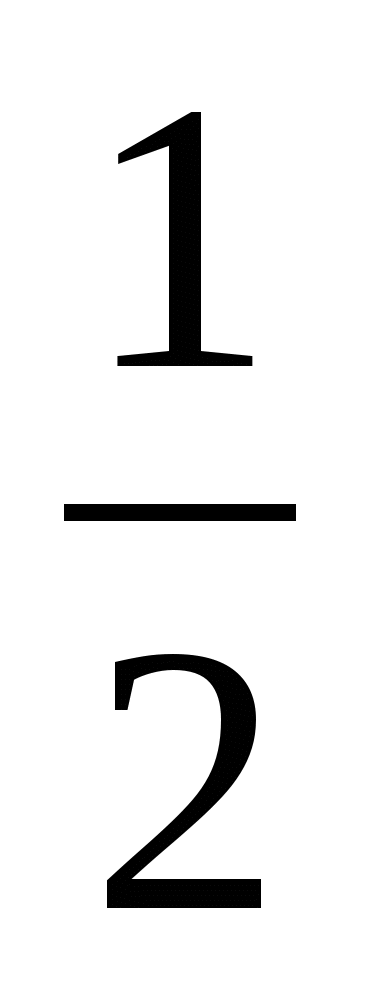 、 、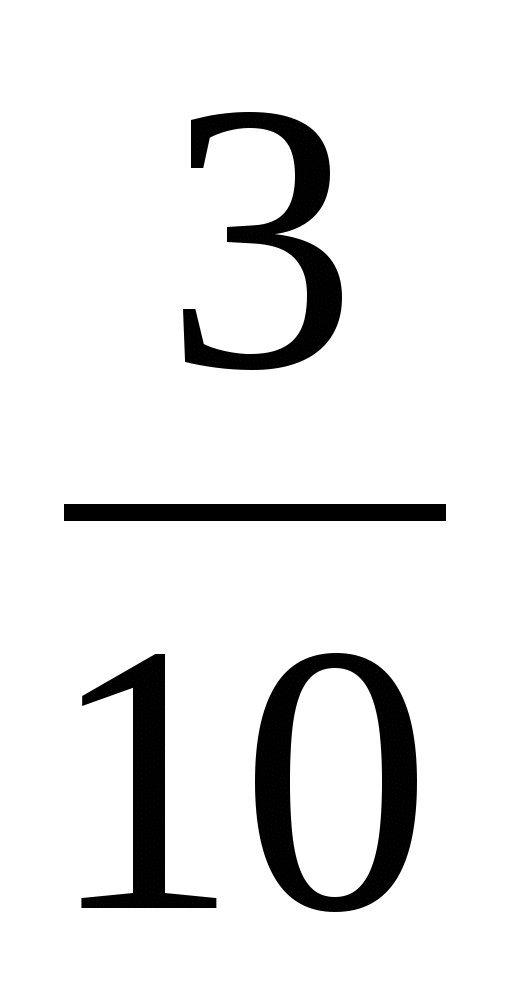 、 、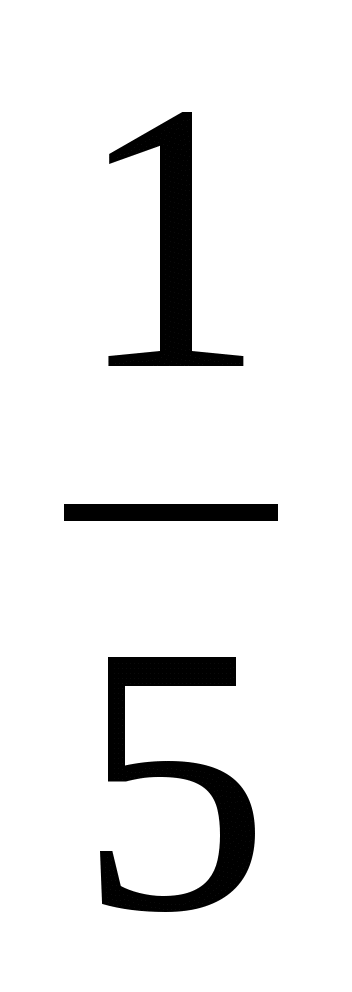 ,且甲厂、乙厂、丙厂次品率依次为0.95、0.94、0.90.从其中任取一件产品,求取到正品的概率. ,且甲厂、乙厂、丙厂次品率依次为0.95、0.94、0.90.从其中任取一件产品,求取到正品的概率. 三、贝叶斯公式 设事件 , , ,…, ,…,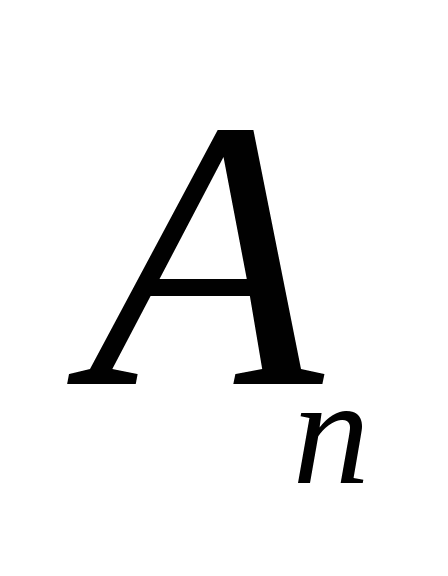 两两互斥, 两两互斥,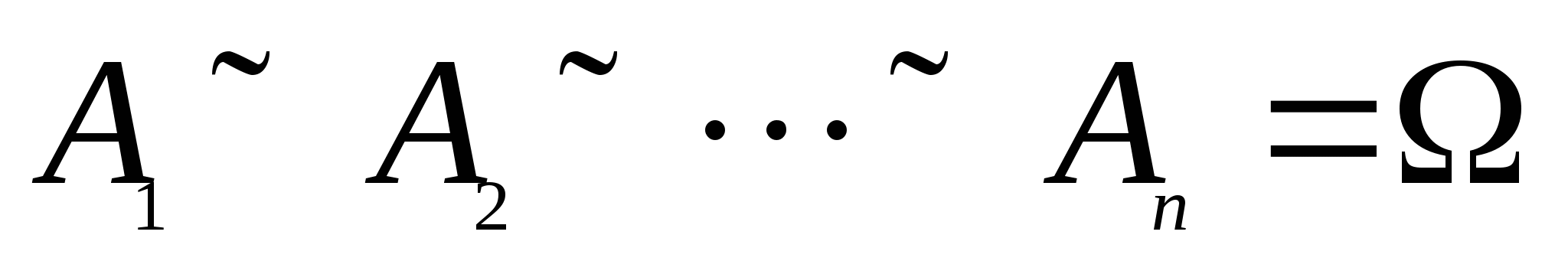 ,且 ,且 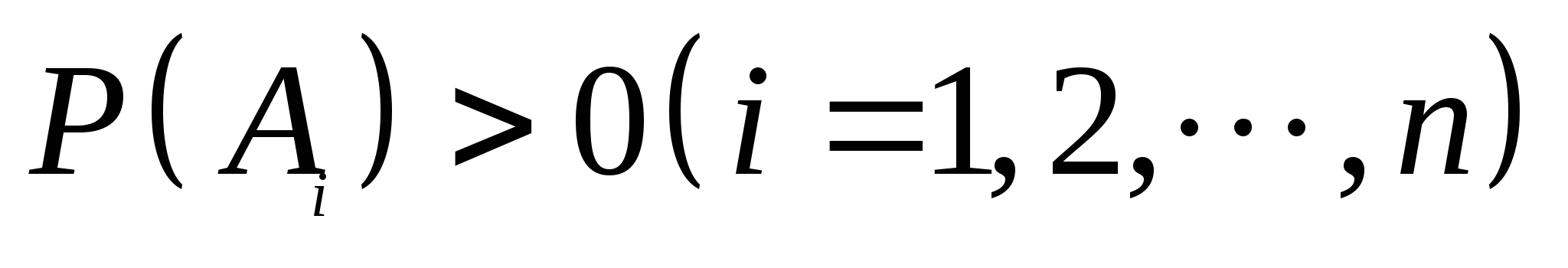 ,对任一事件B, ,对任一事件B,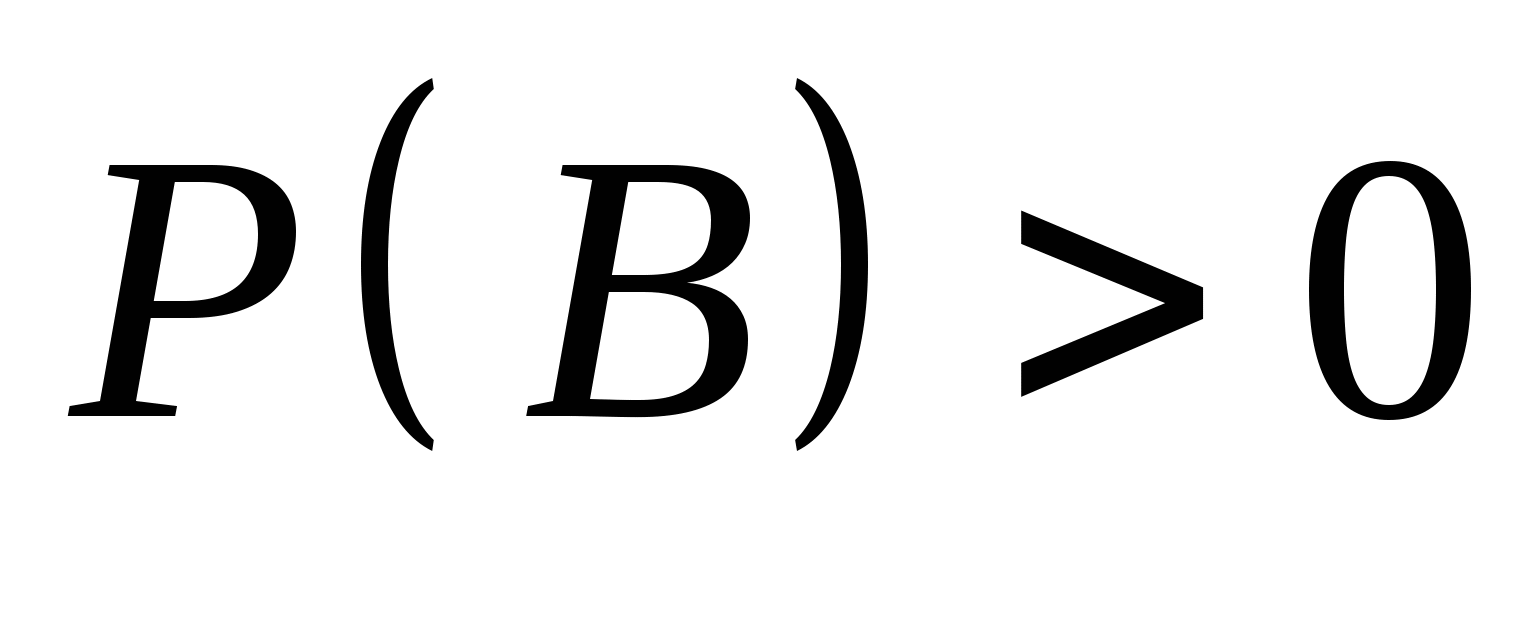 ,则 ,则
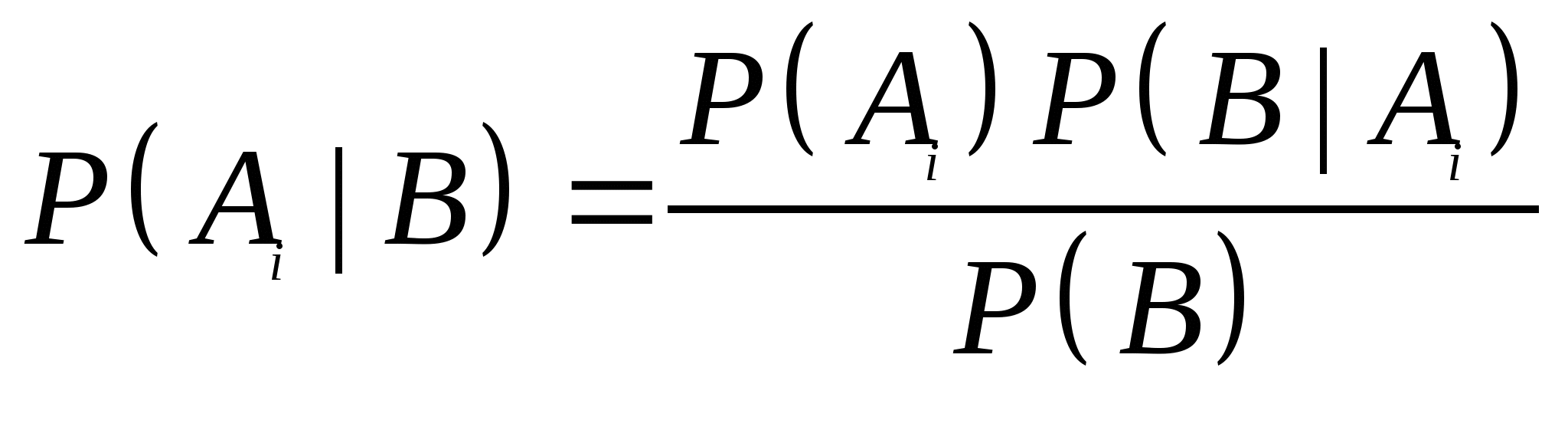
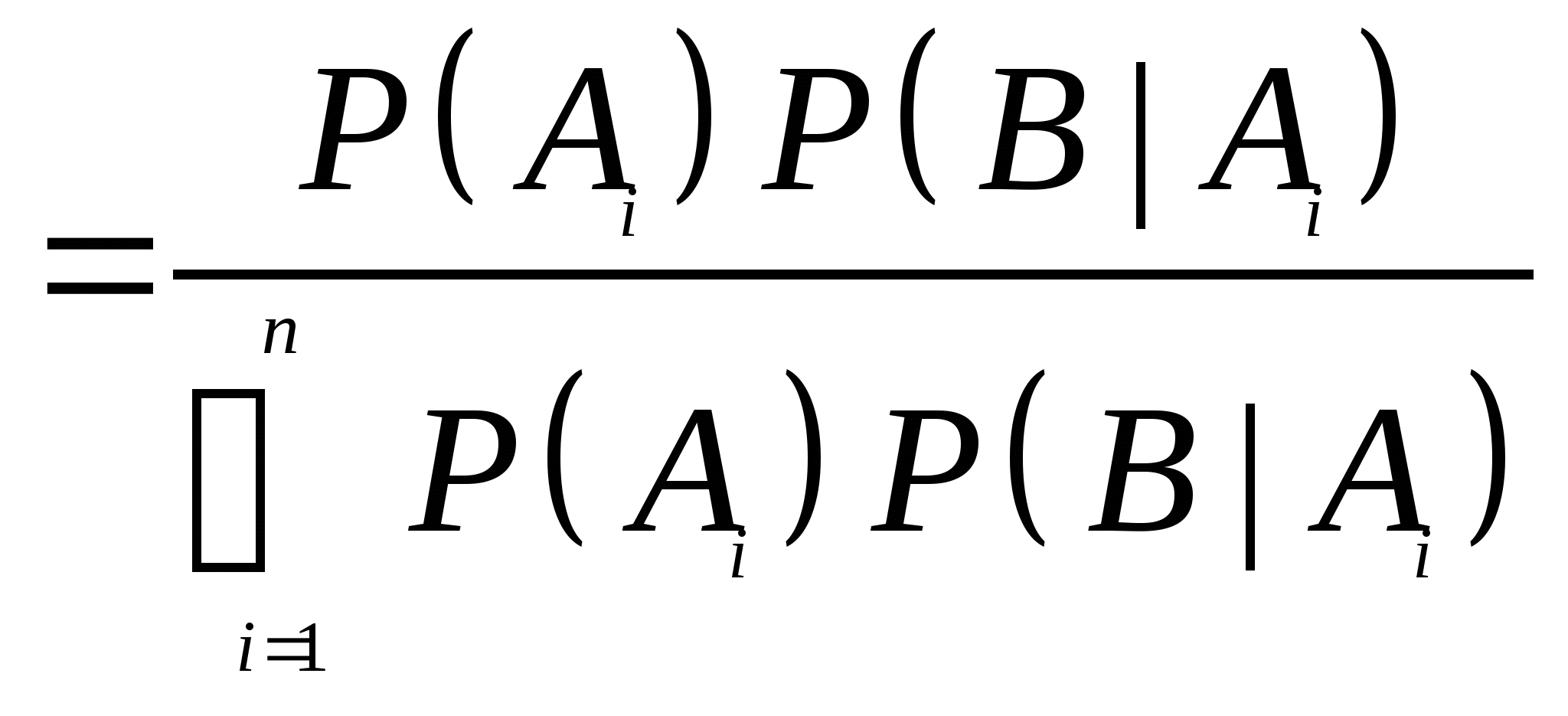 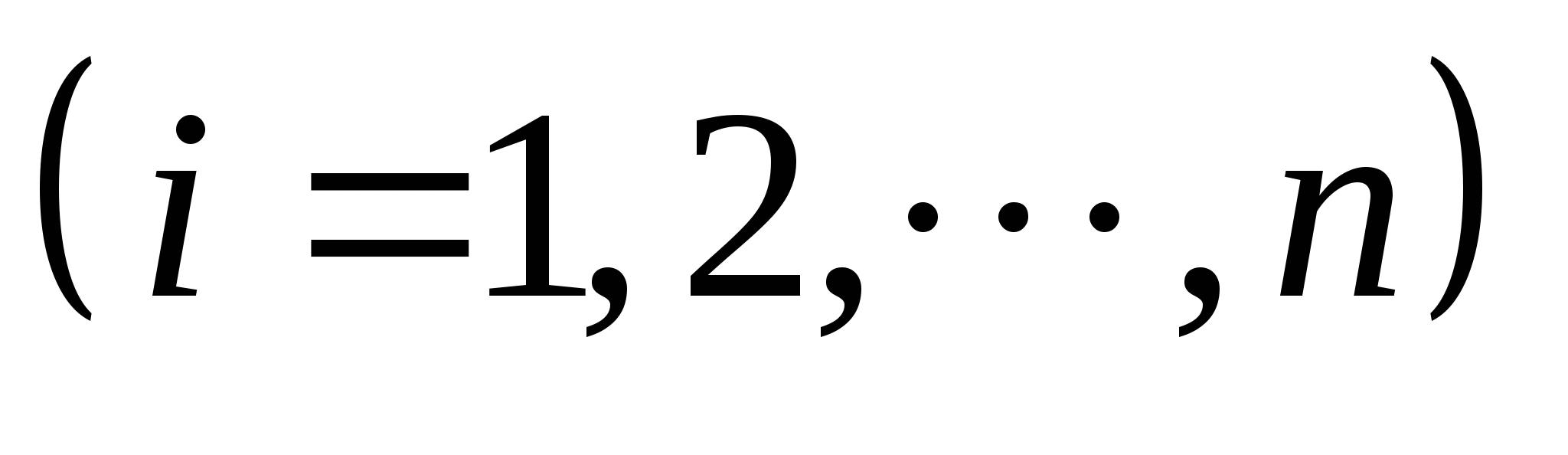 (6) (6)
式叫做贝叶斯公式.
在上面的例4中,取到的一件是正品,问这件产品分别是甲厂、乙厂、丙厂生产的概率各多大?此问题就是分别求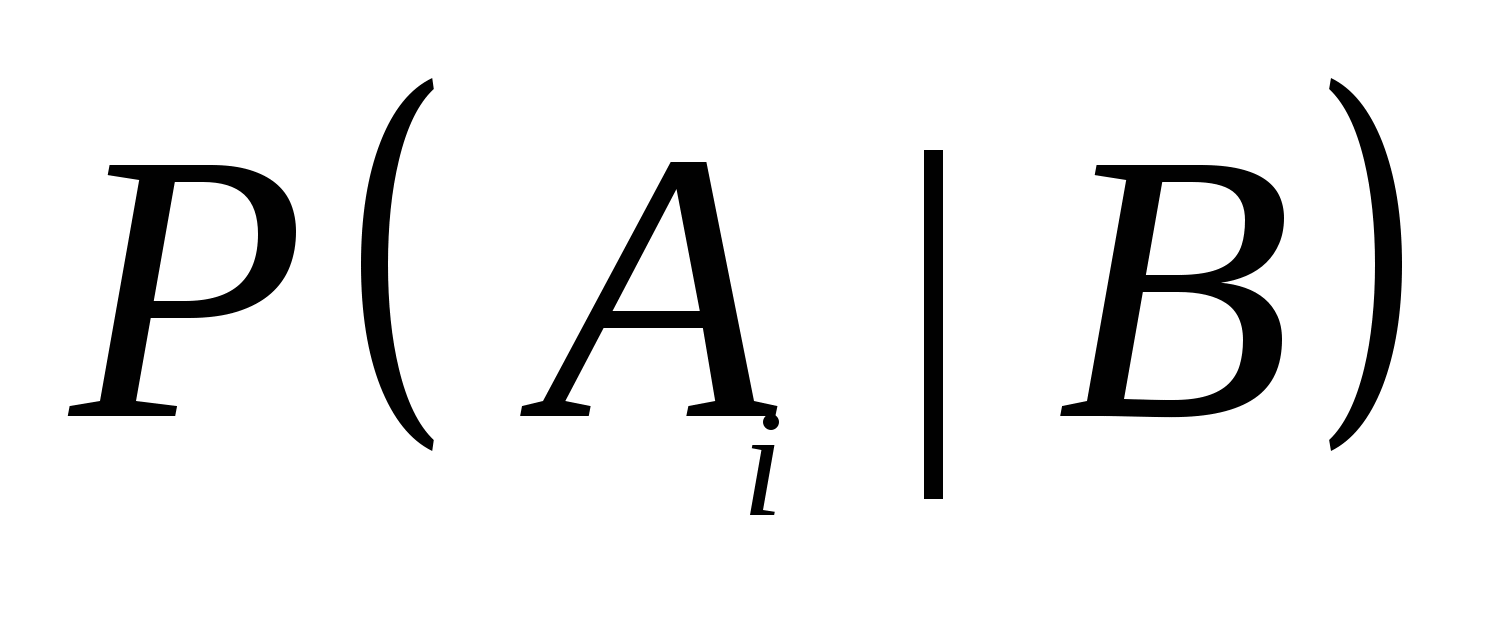 , ,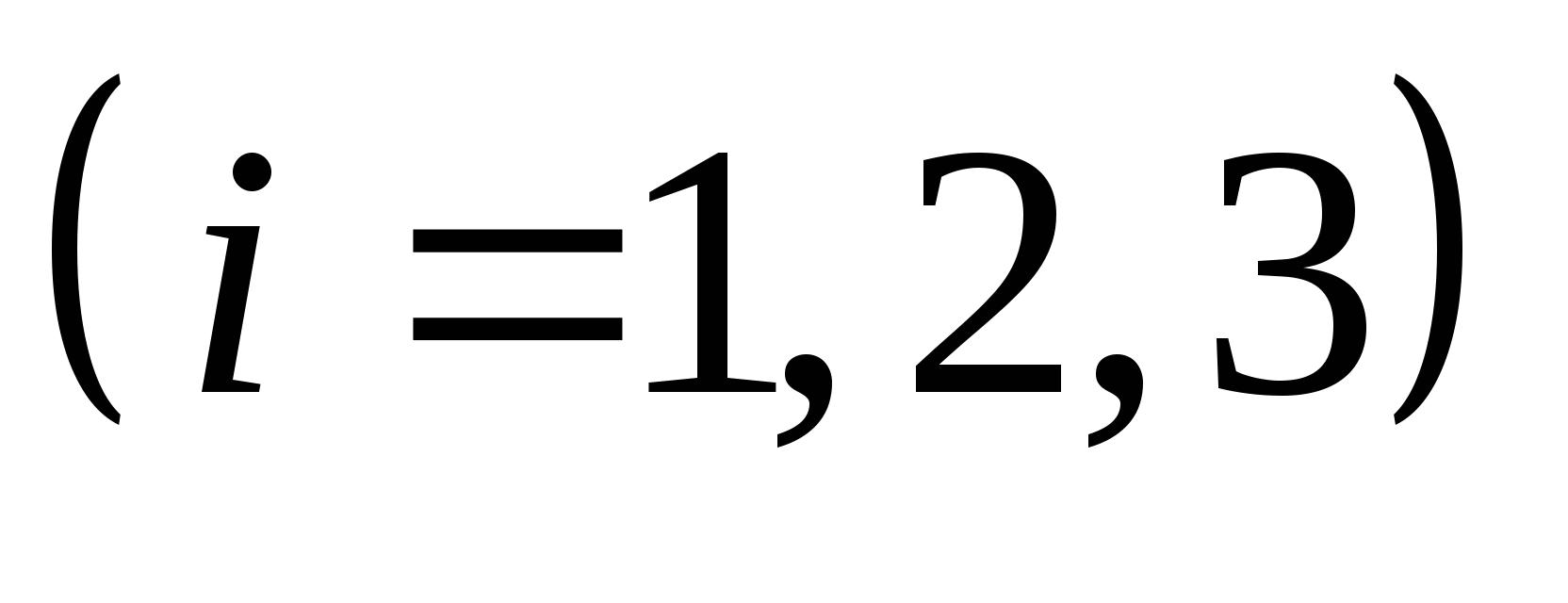 . . 第四节 事件的独立性与二项概率公式 一、事件的相互独立性 定义 如果事件 , , 满足 满足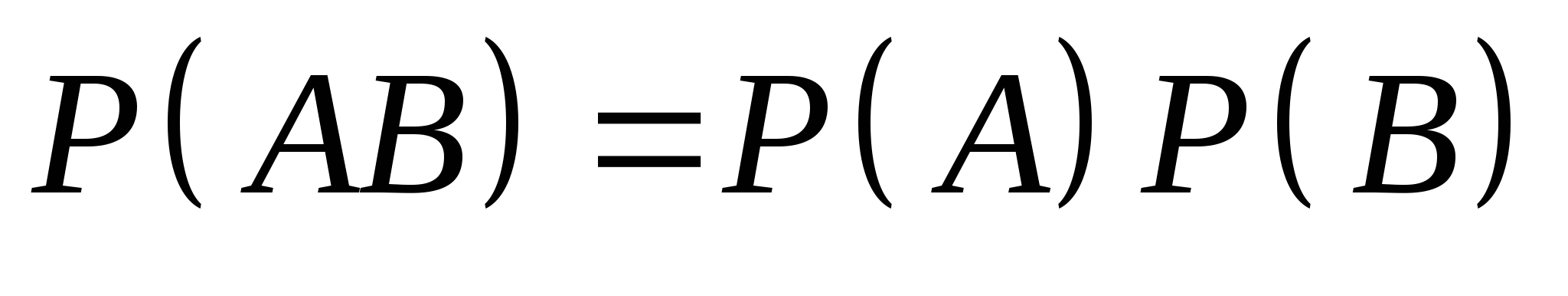 (7) (7) 则称事件 与 与 相互独立,简称 相互独立,简称 , , 独立. 独立. 例1 甲、乙二人独立地向同一目标射击.已知甲、乙二人击中目标的概率分别为0.7和0.8,求目标被击中的概率. 例2 若事件 与 与 相互独立,证明 相互独立,证明 与 与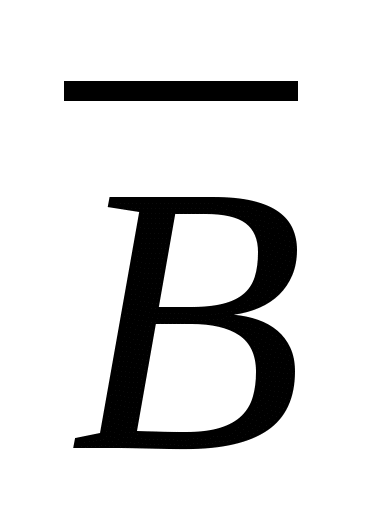 也相互独立. 也相互独立. 设 , , , ,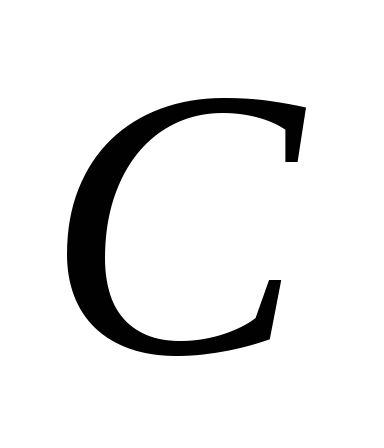 是三个事件,如果满足等式 是三个事件,如果满足等式 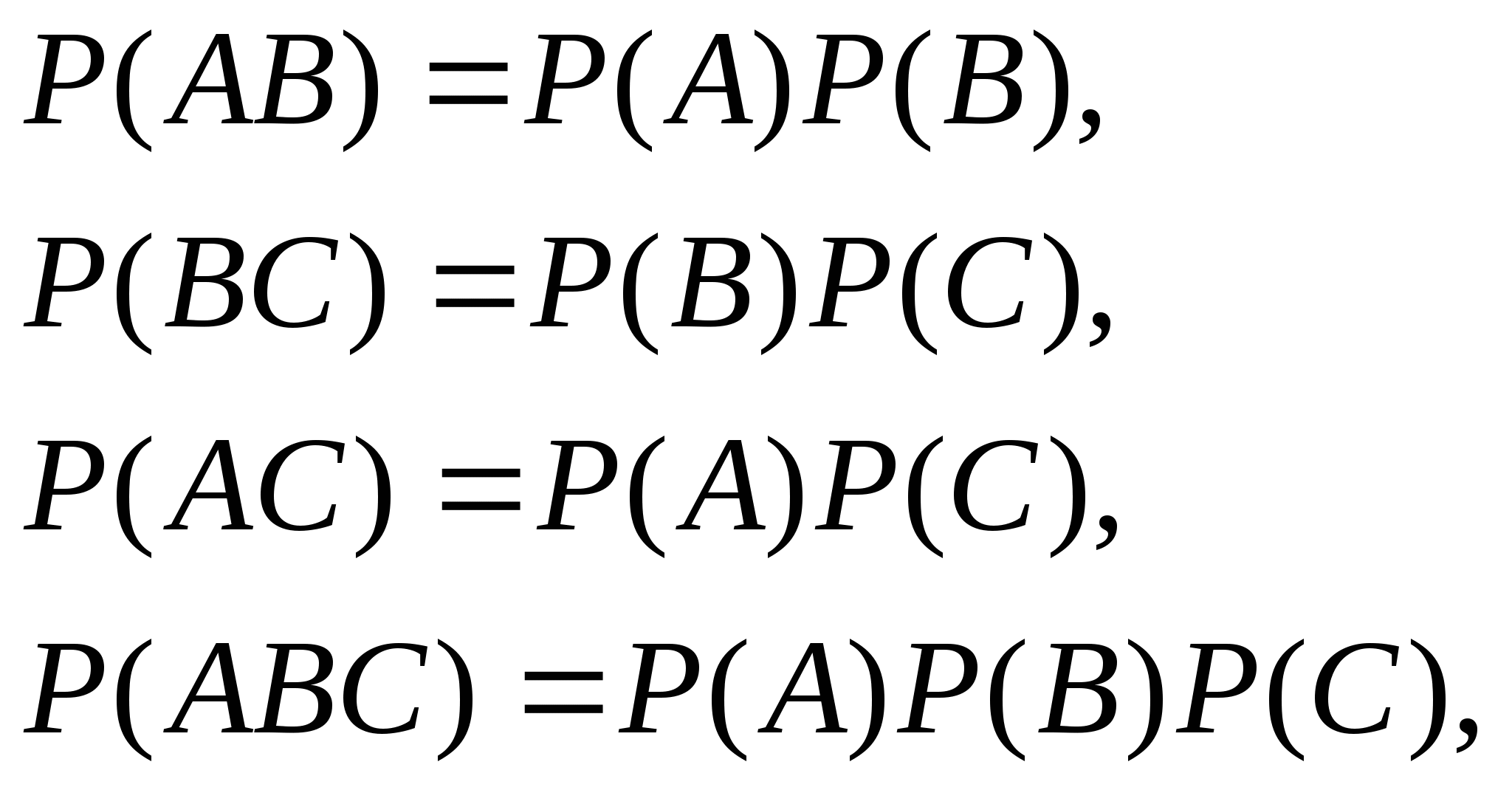 
则称事件 , , , ,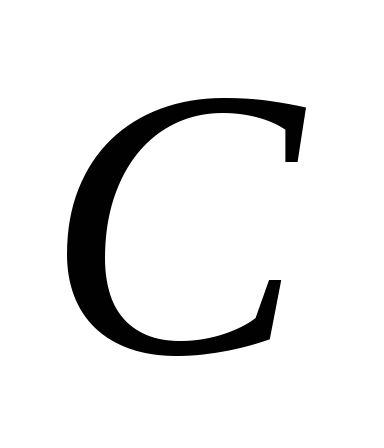 相互独立. 相互独立. 一般地,设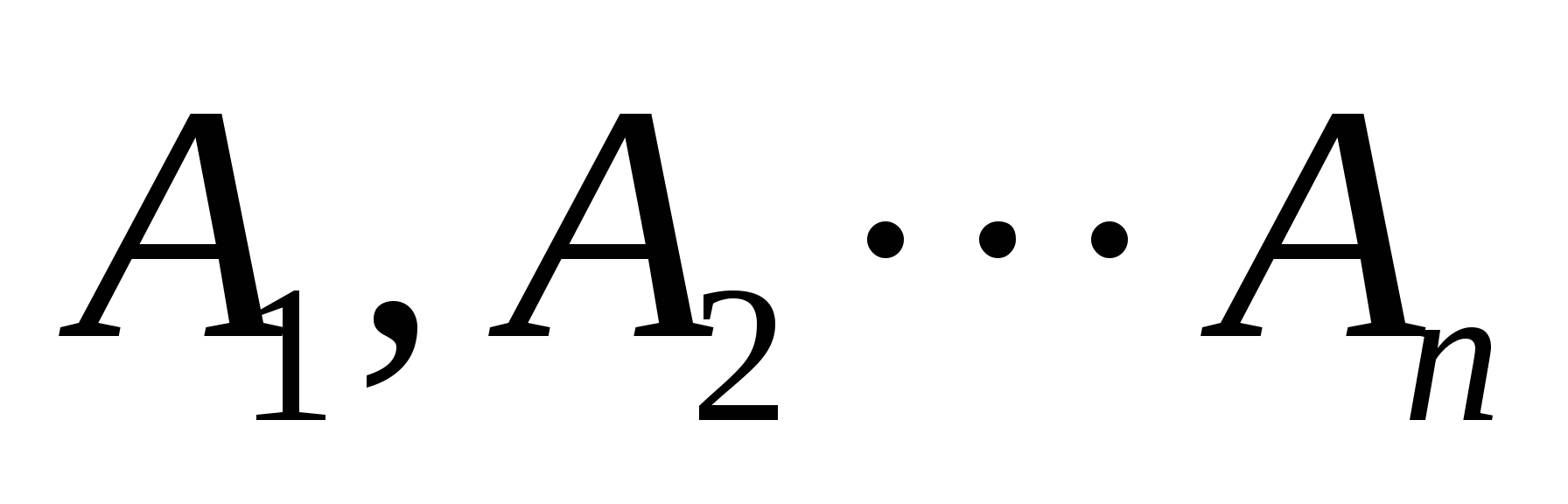 是 是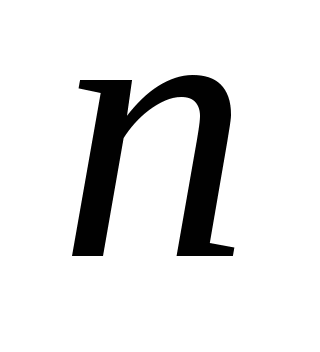 ( (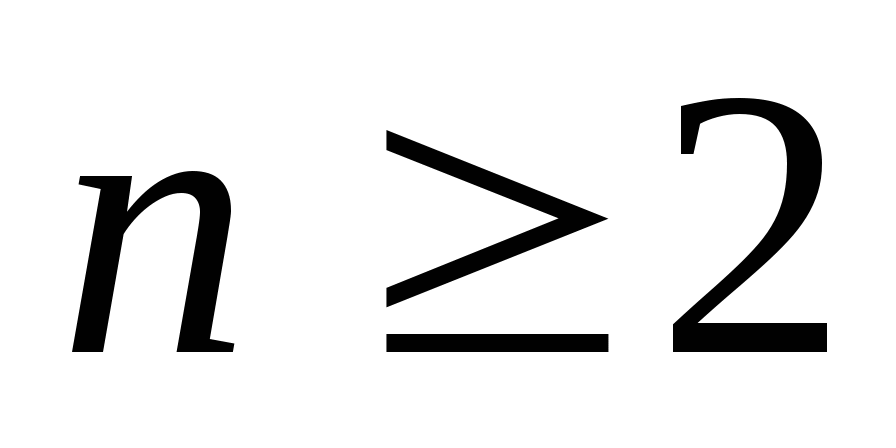 )个事件,如果对于其中任意2个,任意3个,……,任意 )个事件,如果对于其中任意2个,任意3个,……,任意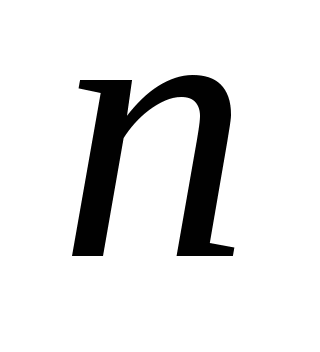 个事件的积事件的概率,都等于各事件概率之积,则称为事件 个事件的积事件的概率,都等于各事件概率之积,则称为事件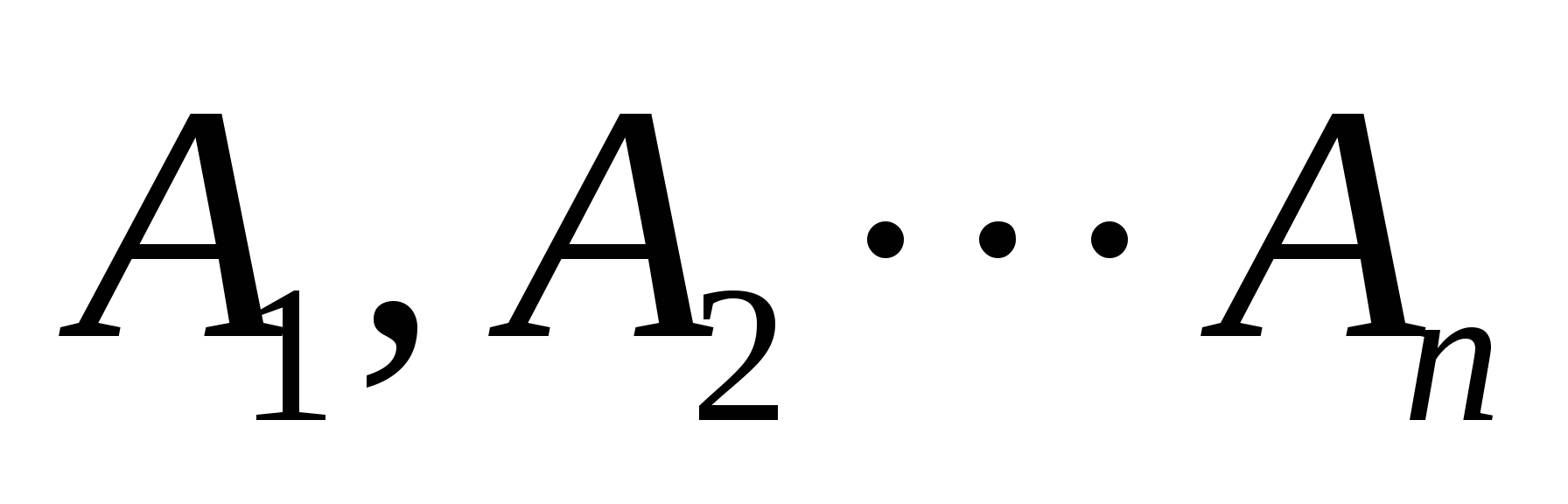 相互独立. 相互独立. 由此即可得到以下两个重要结论: (i)若事件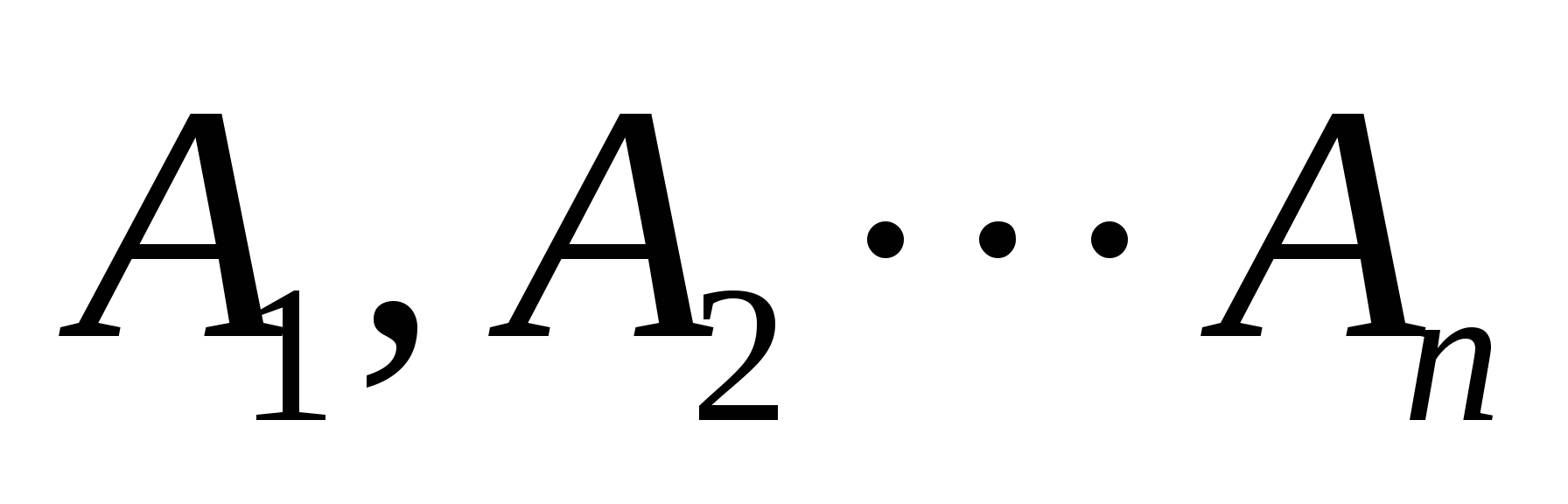 ( (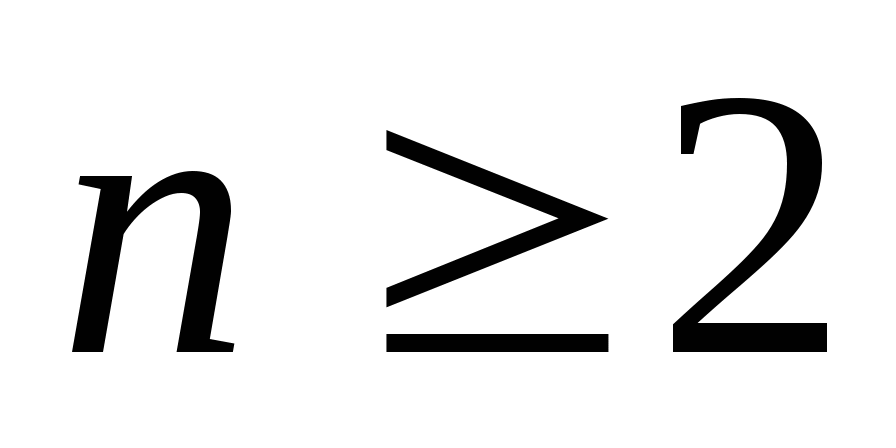 )相互独立,则其中任意 )相互独立,则其中任意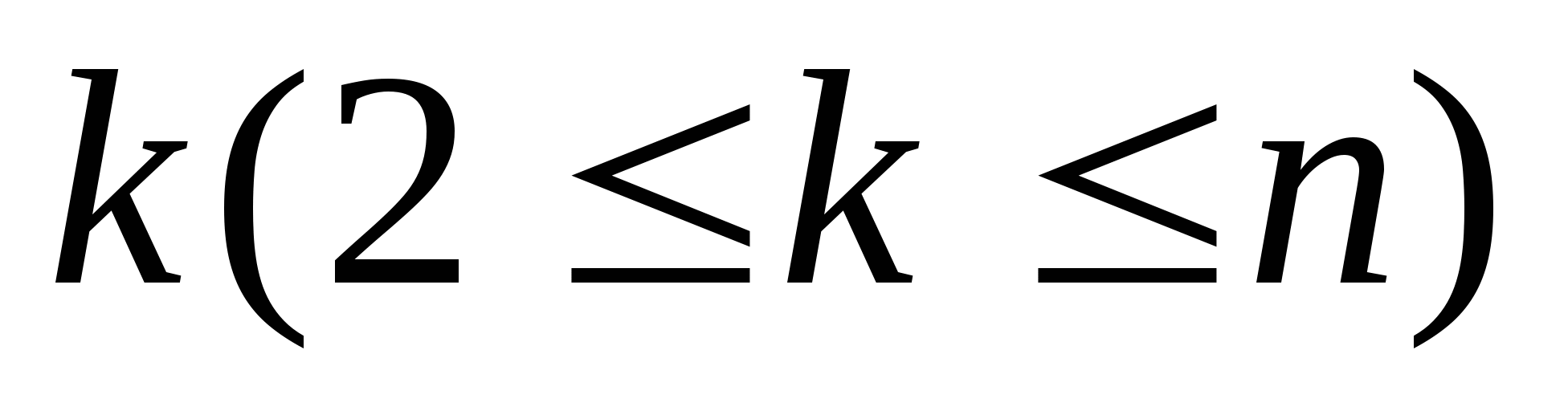 个事件也是相互独立的. 个事件也是相互独立的. (ii) 若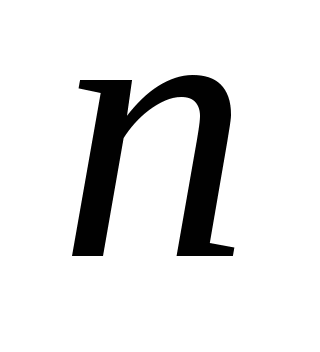 个事件 个事件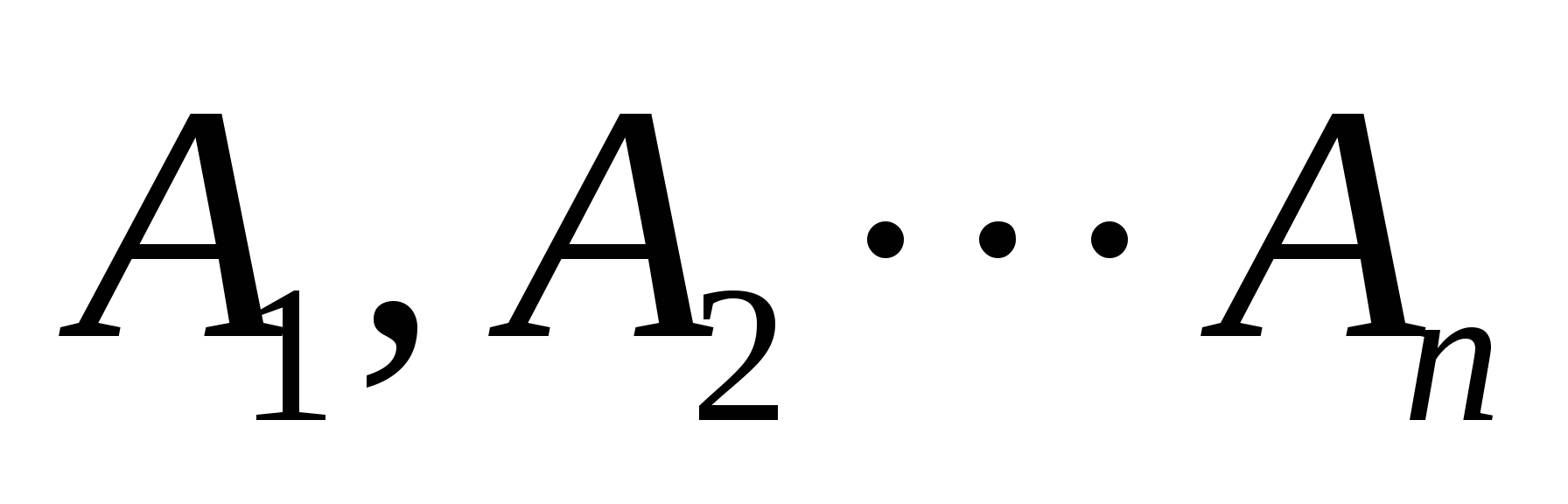 ( (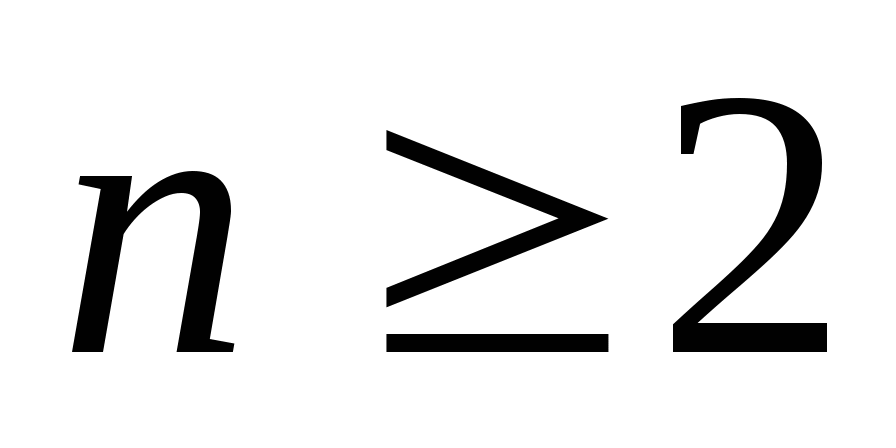 )相互独立,则将 )相互独立,则将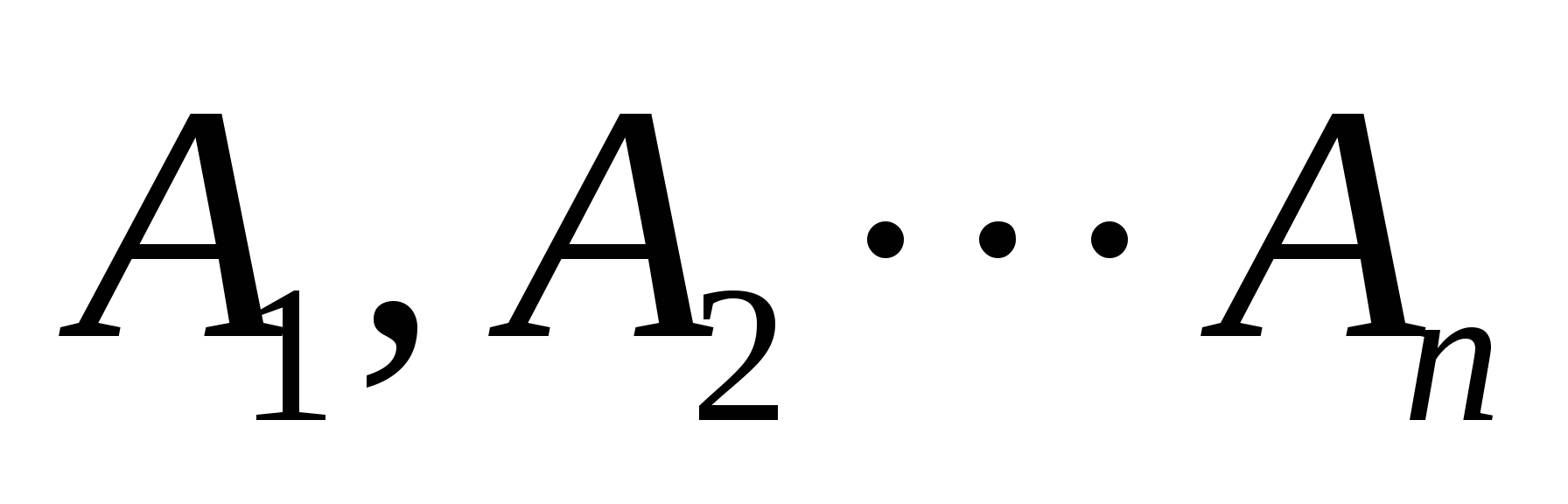 中任意多个事件换成其对立事件仍是独立的. 中任意多个事件换成其对立事件仍是独立的. 若事件 , , ,…, ,…,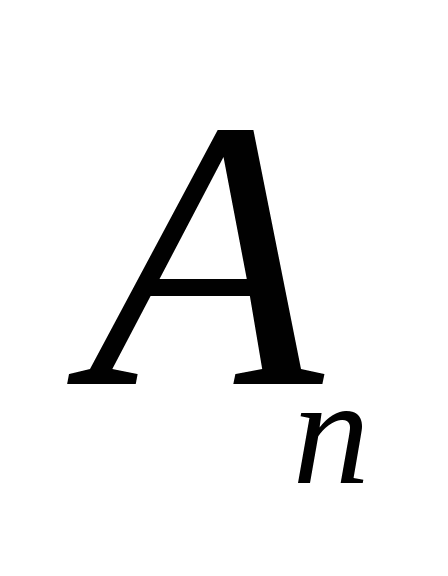 相互独立,则有 相互独立,则有 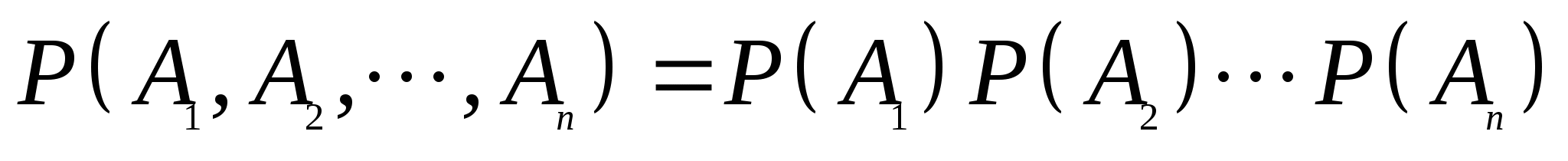
每次试验出现的结果互不影响,这类试验叫做重复独立试验.在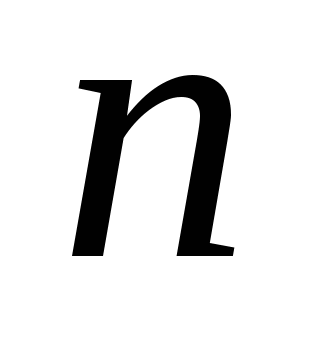 次重复独立试验中,若每次结果只有两个, 次重复独立试验中,若每次结果只有两个, 或 或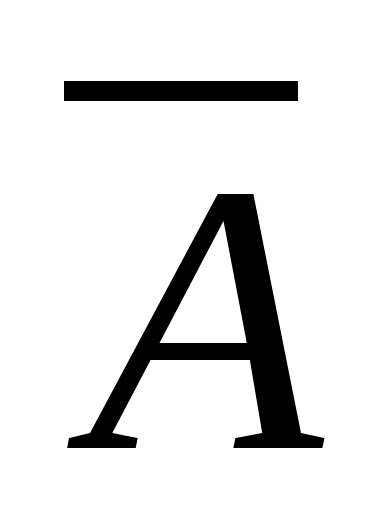 ,则将此类试验叫做 ,则将此类试验叫做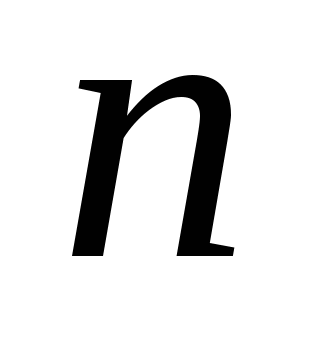 重贝努利试验,这种概率模型叫做贝努利概型. 重贝努利试验,这种概率模型叫做贝努利概型. 2. 二项概率 在贝努利概型中,设事件 发生的概率为 发生的概率为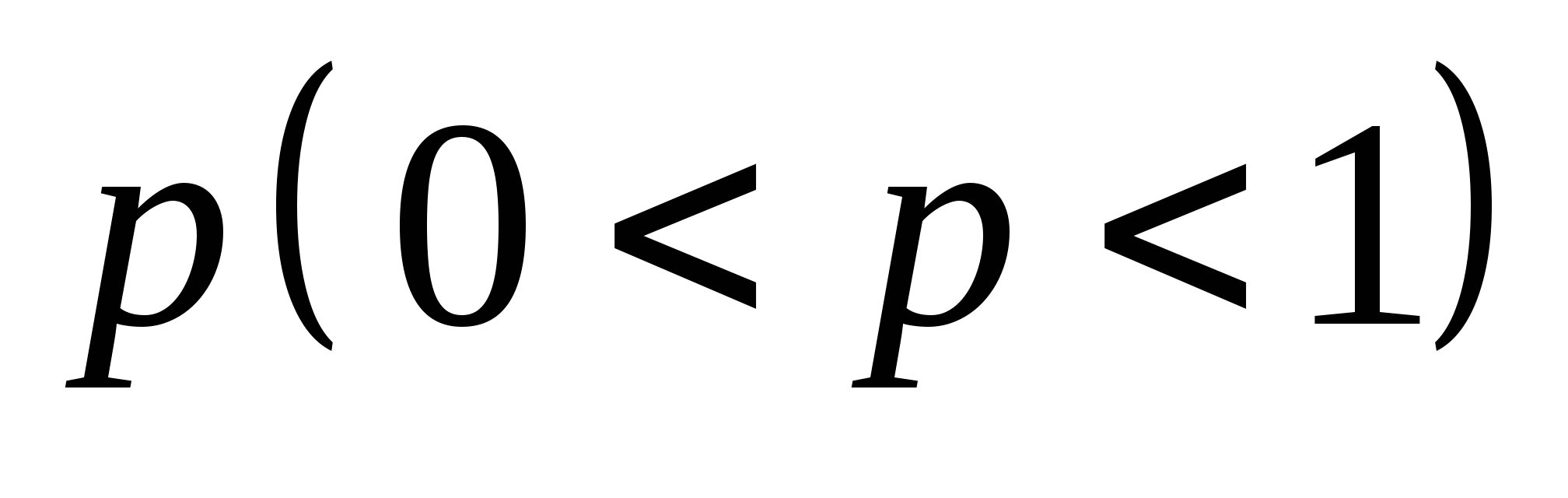 ,则在这 ,则在这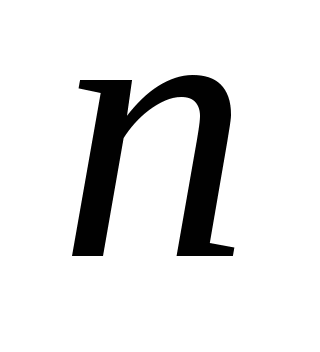 次试验中事件 次试验中事件 恰好发生 恰好发生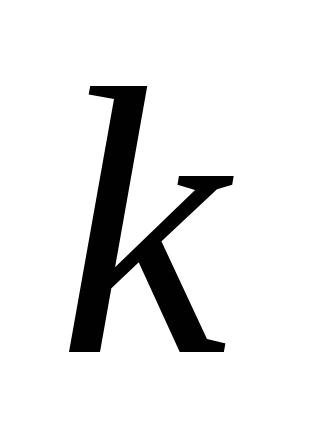 次的事件为 次的事件为
k个 n-k个 k个 n-k个 n-k+1个 k-1个
  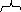  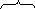 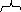
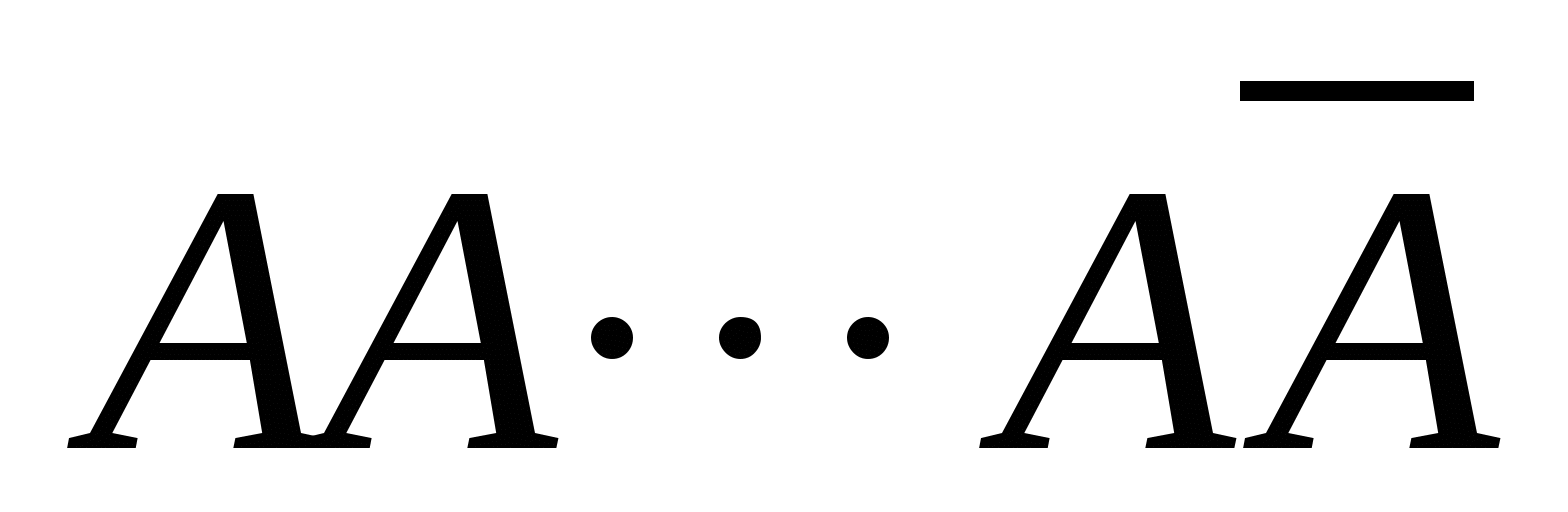 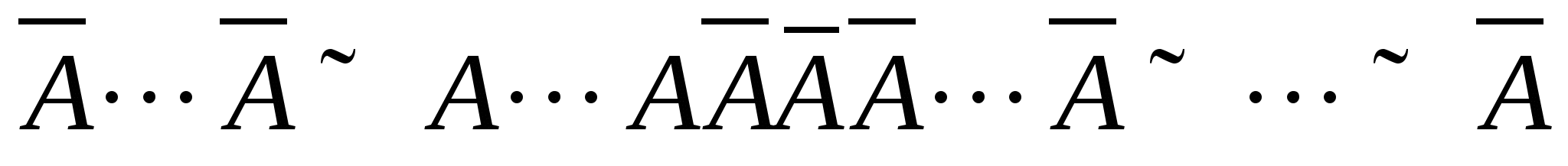 
这是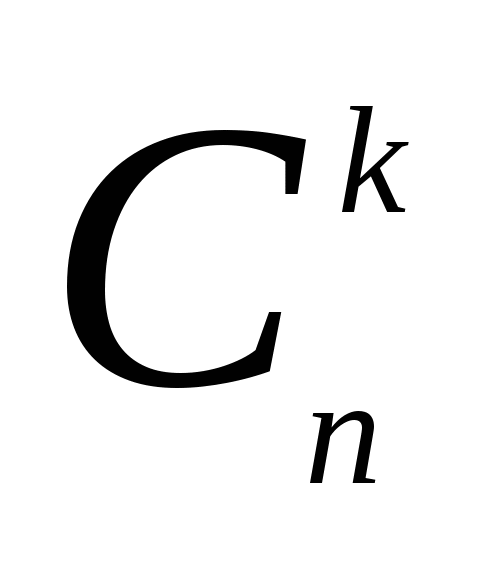 个互斥事件的和,且每一个事件的概率均为 个互斥事件的和,且每一个事件的概率均为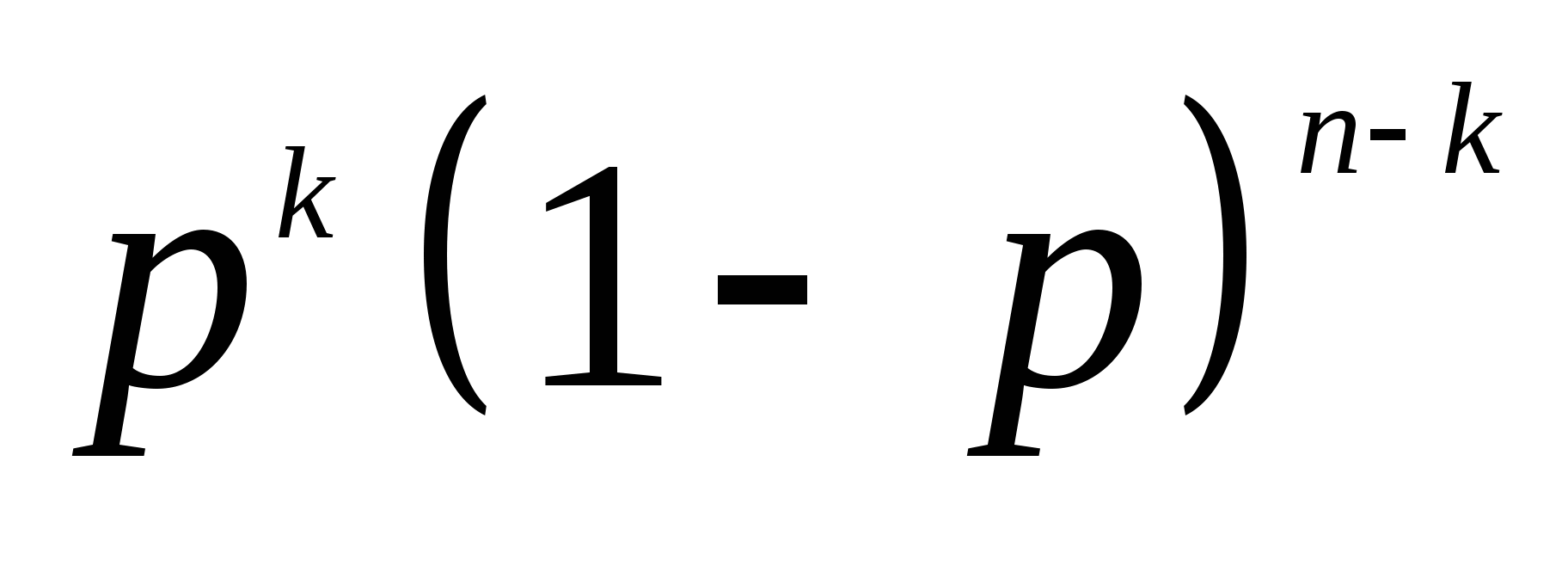 ,所以在 ,所以在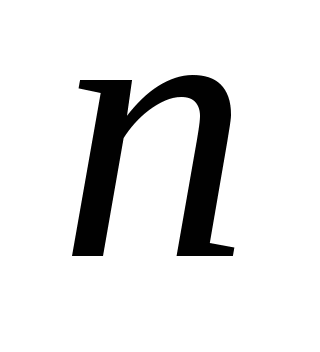 次重复独立试验中事件 次重复独立试验中事件 发生 发生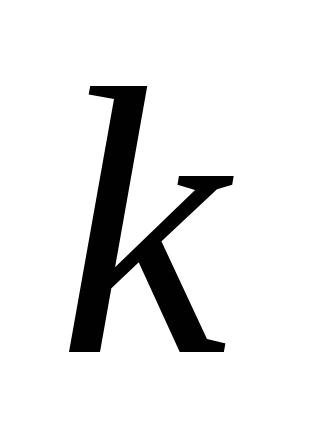 次的概率为 次的概率为 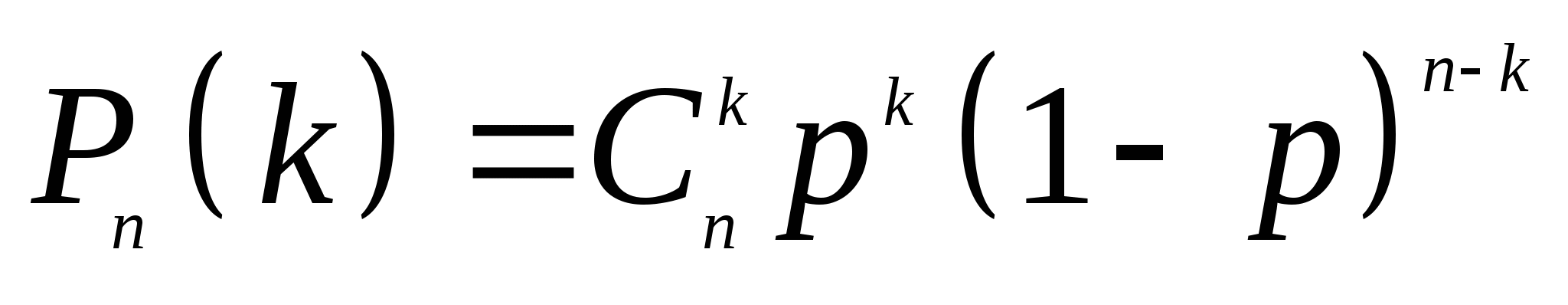 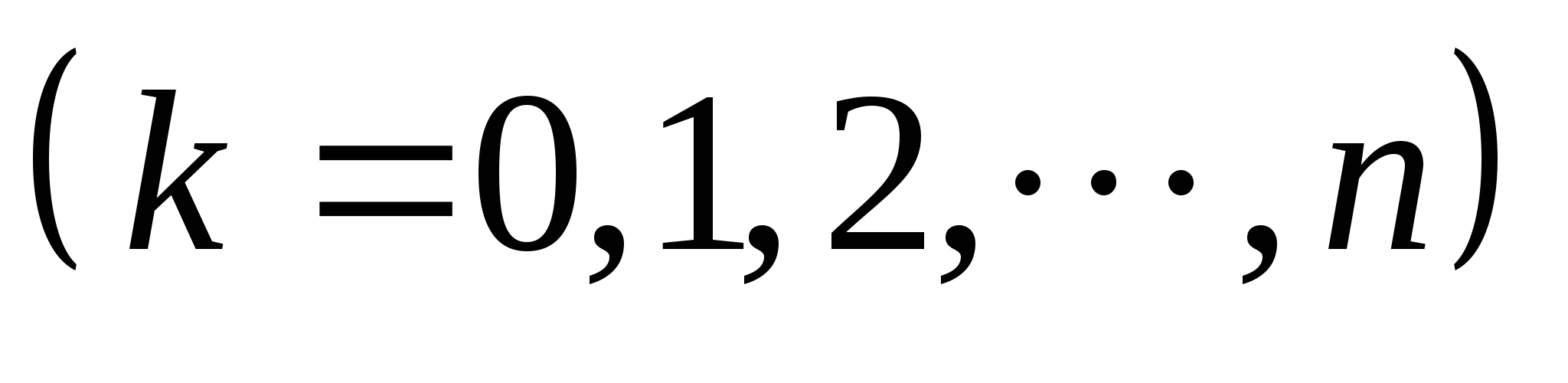 (8) (8)
(8)式叫做二项概率公式. 例4 在10件产品中有2件次品,从中每次取一件,有放回地取三次,求恰好有两件次品的概率. 贝努里概型对试验结果没有等可能的要求,但有下述要求: (1)每次试验条件相同; (2)每次试验只考虑两个互逆结果A或 ,且P(A)=p, ,且P(A)=p, (3)各次试验相互独立. 可以简单地说,二项分布描述的是n重贝努里试验中出现“成功”次数X的概率分布. 这一讲,我们介绍了事件独立性的概念.不难发现,当事件相互独立时,乘法公式变得十分简单,因而也就特别重要和有用. 如果事件是独立的,则许多概率的计算就可大为简化.需要指出的是,不少复杂事件概率的计算是上面两讲的加法公式和乘法公式的综合运用和推广. 第二章 随机变量及其分布 教学基本要求: 理解随机变量概念 离散型随机变量及概率函数(分布律)的概念和性质 连续型随机变量及概率密度函数的概念 理解分布函数的概念和性质 会利用概率分布计算有关事件的概率 掌握两点分布、二项分布、泊松分布、超几何分布、几何分布和指数分布 会求简单随机变量函数的分布。
重点: 离散型、连续型随机变量概念 分布函数概念和性质 概率密度函数概念和性质 几个重要的随机变量 简单随机变量函数的分布。
难点: 1、随机变量函数的分布。 第一节 离散型随机变量及分布律 一、离散型随机变量的分布律 定义1 若随机变量 的所有可能取值为 的所有可能取值为 ,且 ,且 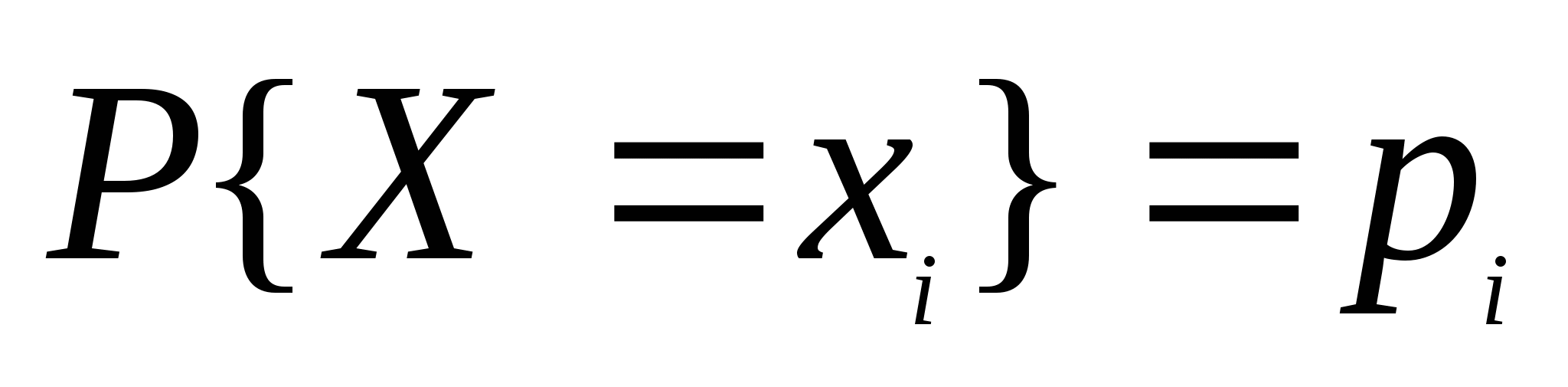 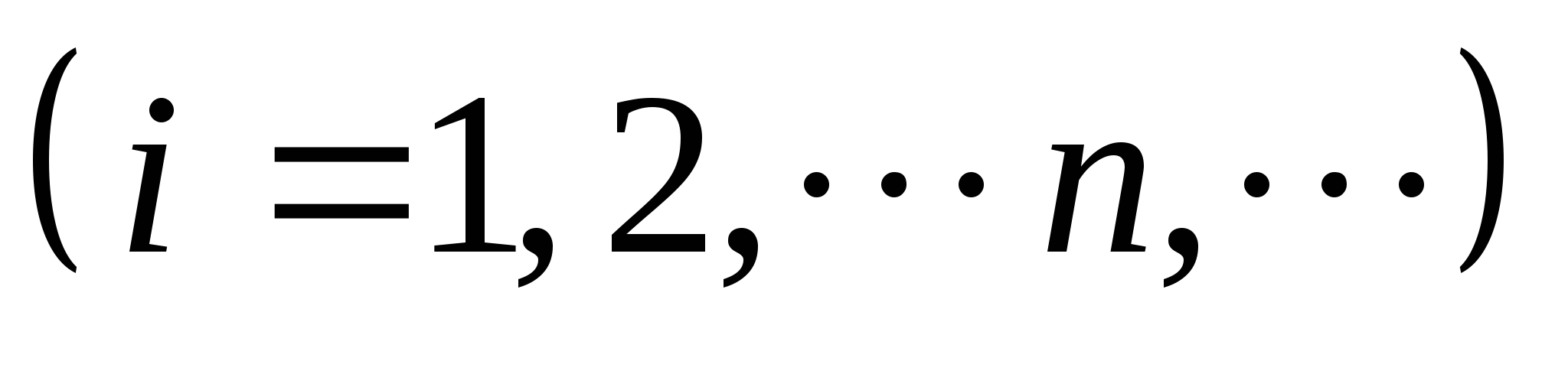 (1) (1)
存在,则称 为离散型随机变量,并称(1)为离散型随机变量 为离散型随机变量,并称(1)为离散型随机变量 的概率分布或分布律(列). 的概率分布或分布律(列). 分布律也可用表格表示为   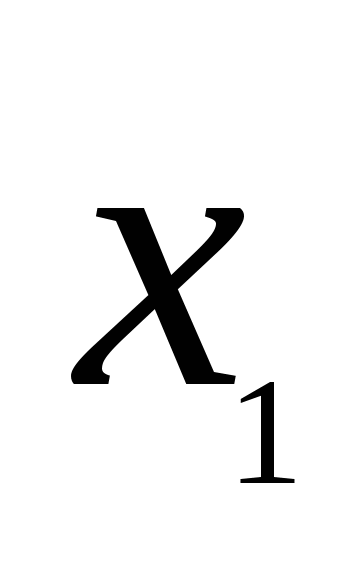 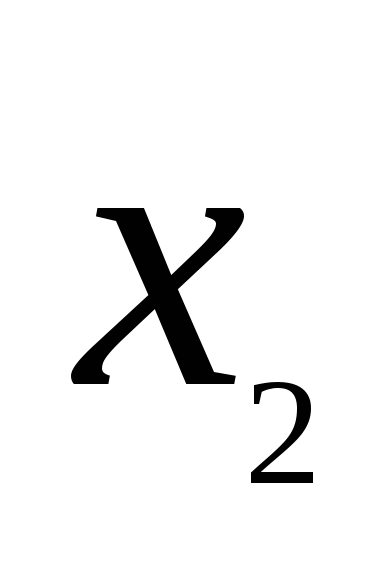 ┅ ┅ 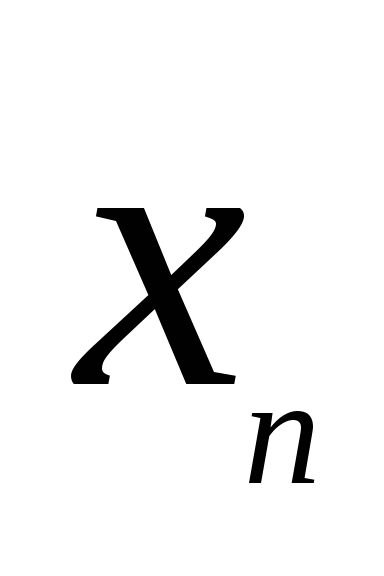 ┅ ┅
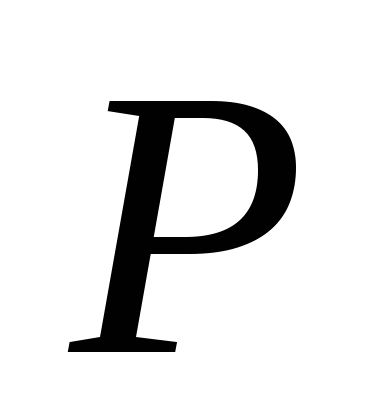  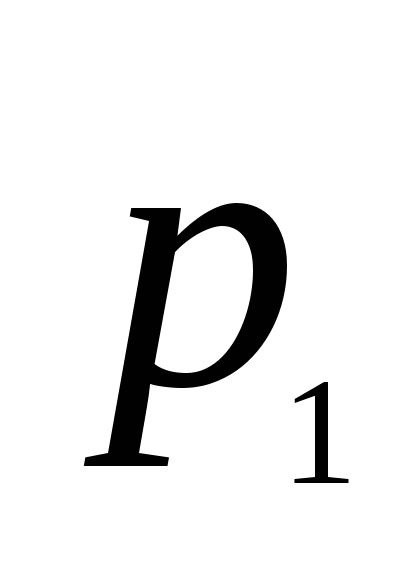 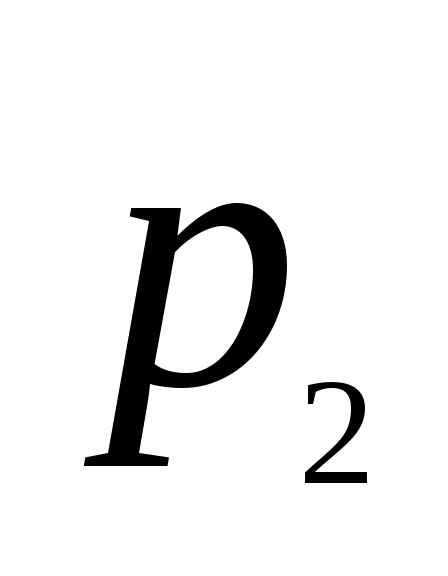 ┅ ┅ 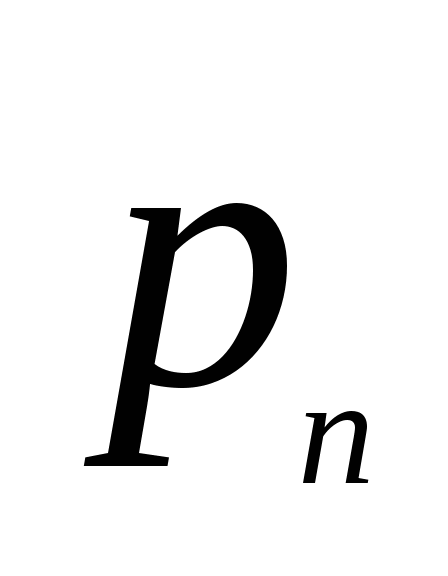 ┅ ┅
由概率定义知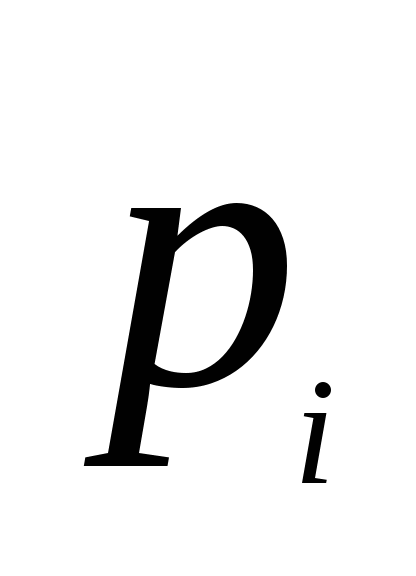 满足下述两个条件: 满足下述两个条件: (1)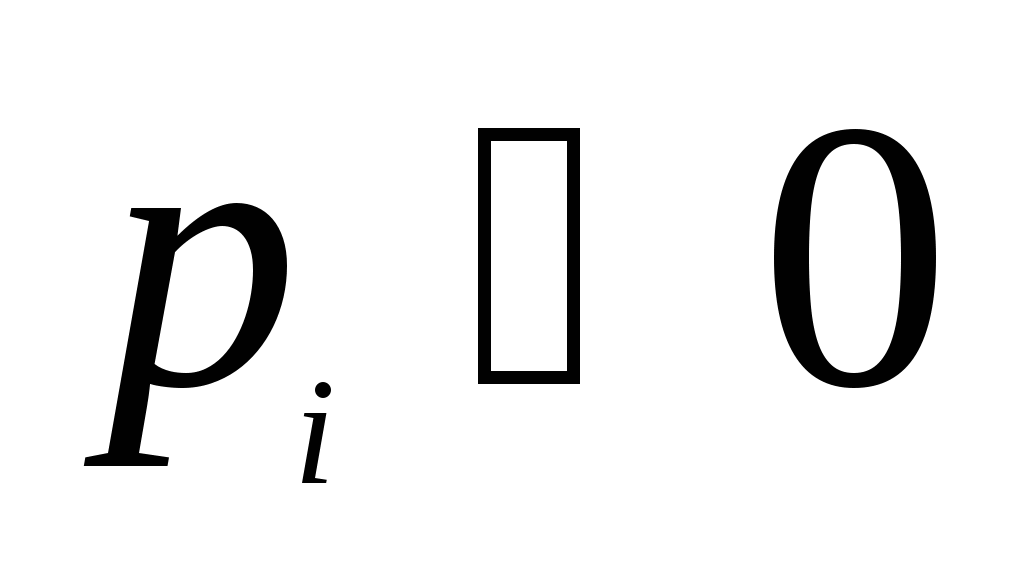 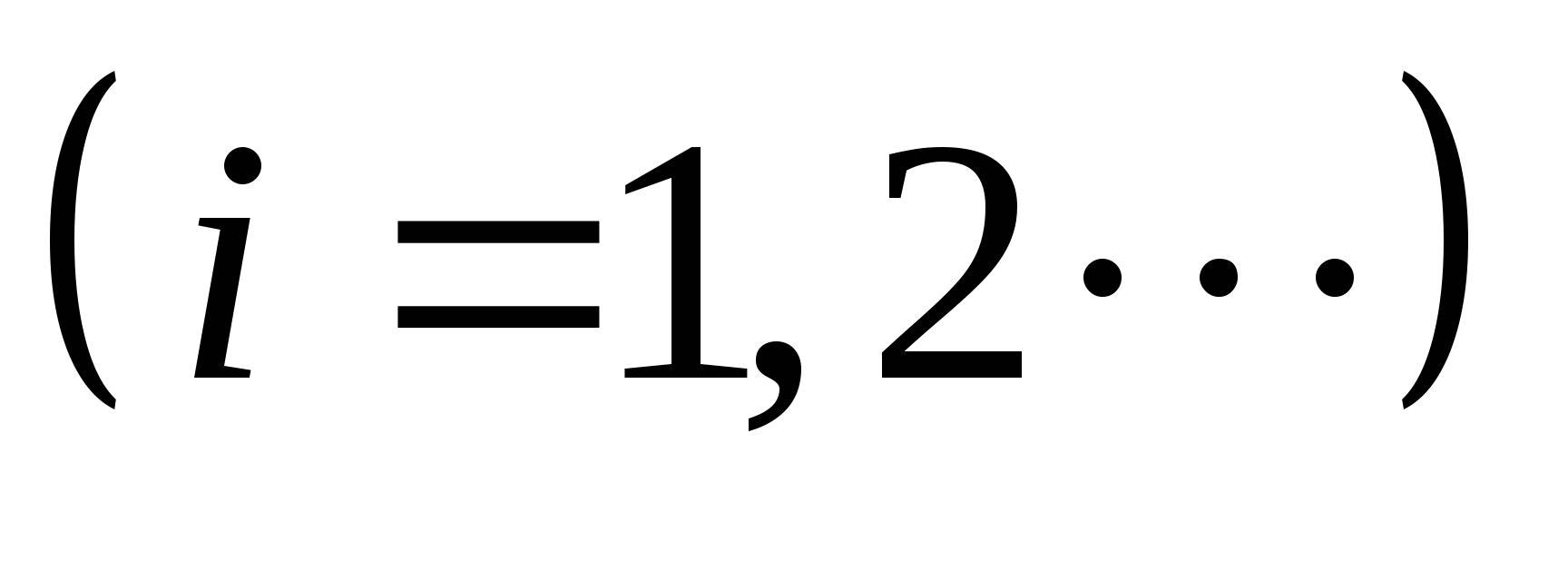 ; (2) ; (2)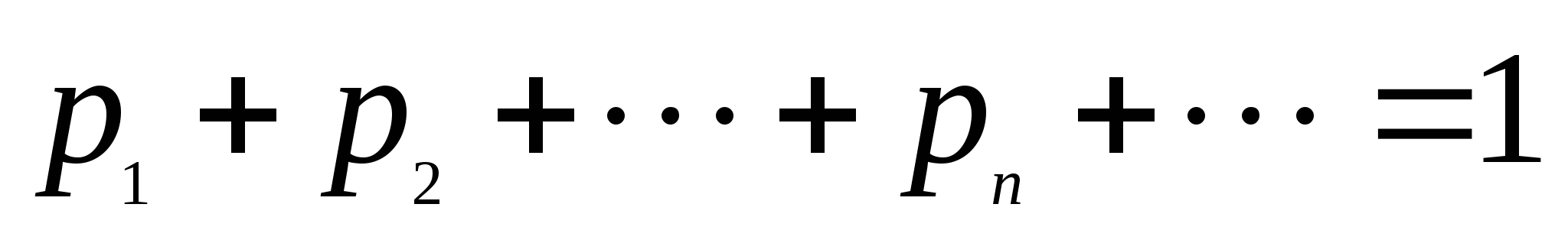 . . 例1 在有2件次品,8件正品的产品中,任取三件,则取得的次品数 是随机变量,求 是随机变量,求 的分布律. 的分布律. 二、几个常用的离散型随机变量的分布 1.(0—1)分布 若随机变量 的分布律为 的分布律为   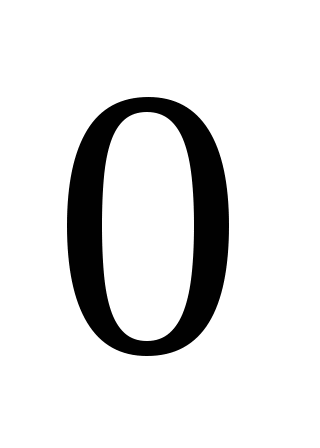 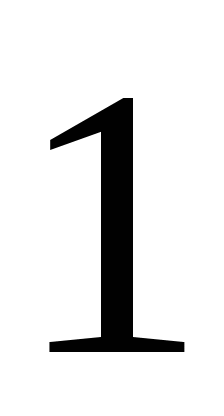
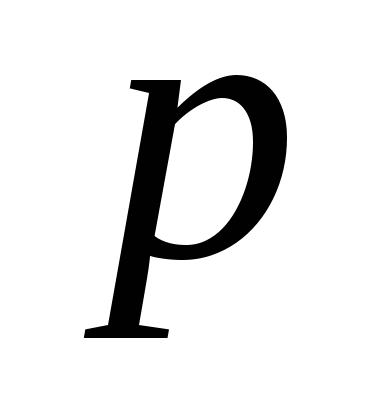  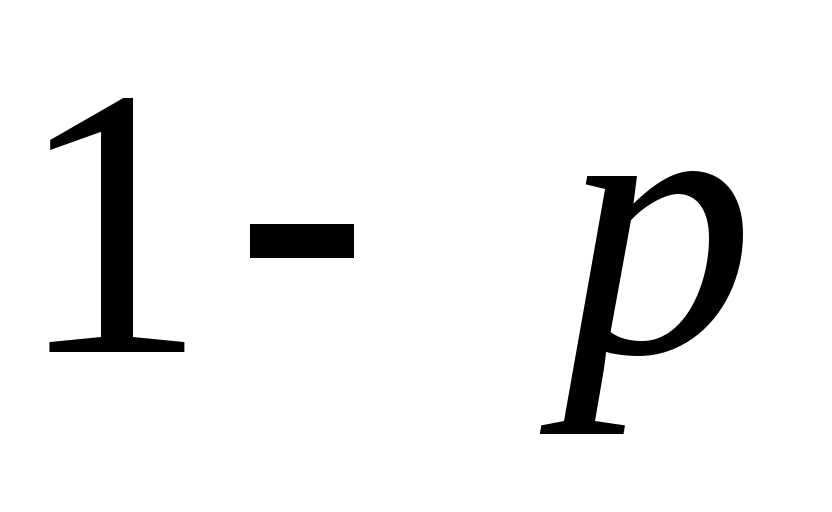 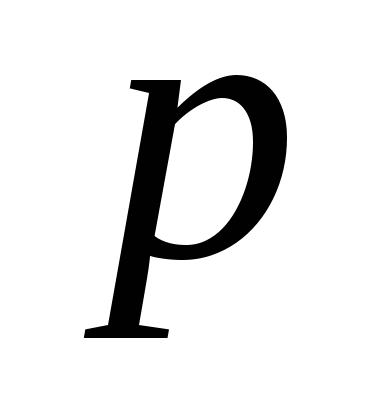 ( (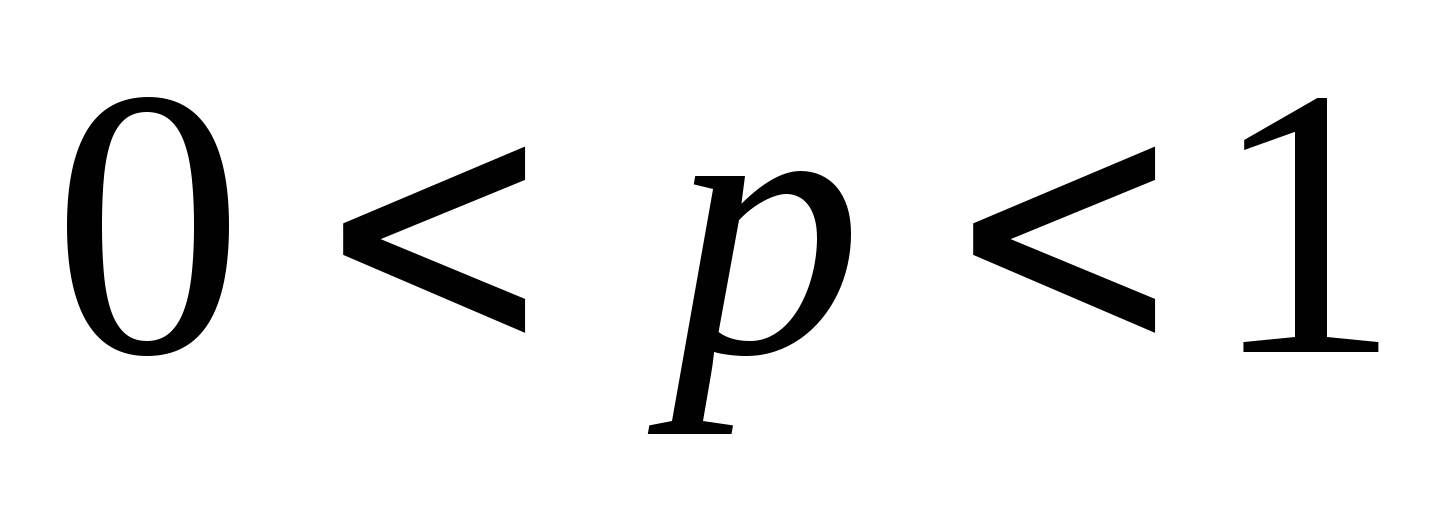 ) )
则 称 称 服从于(0—1)分布.记作 服从于(0—1)分布.记作 ~(0—1). ~(0—1). 例 2 在次品率为5%的一批产品中,任取一件,则取得次品数 2 在次品率为5%的一批产品中,任取一件,则取得次品数 的分布律为 的分布律为  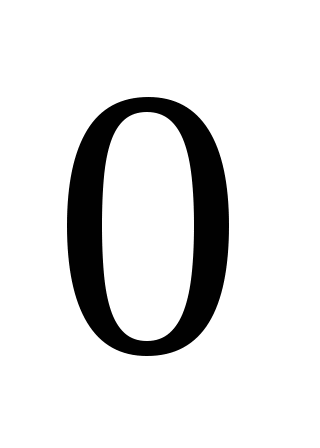 1 1
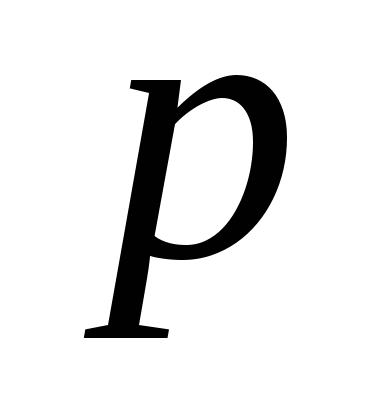  0.95 0.05 0.95 0.05
故 服从(0—1)分布. 服从(0—1)分布. 2.二项分布 若随机变量 的分布律为 的分布律为 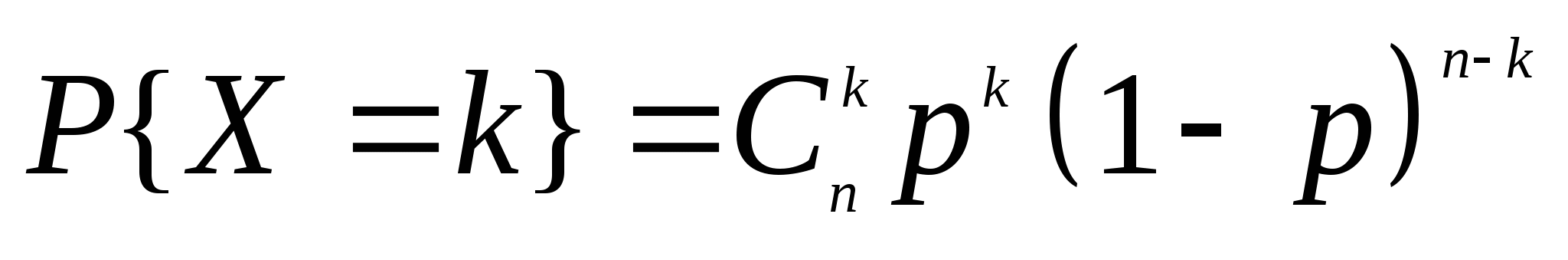 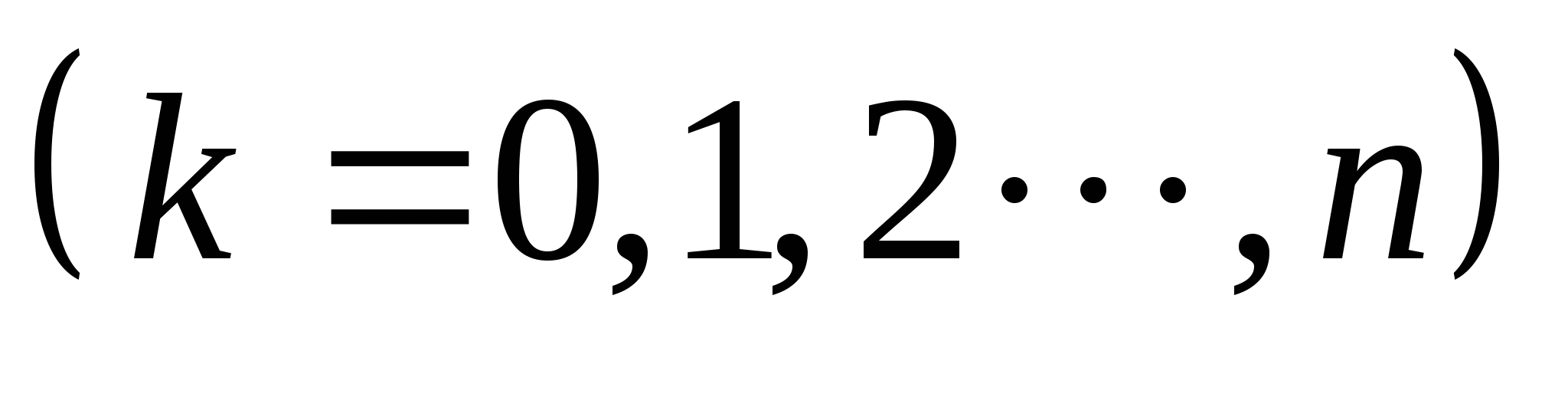
其中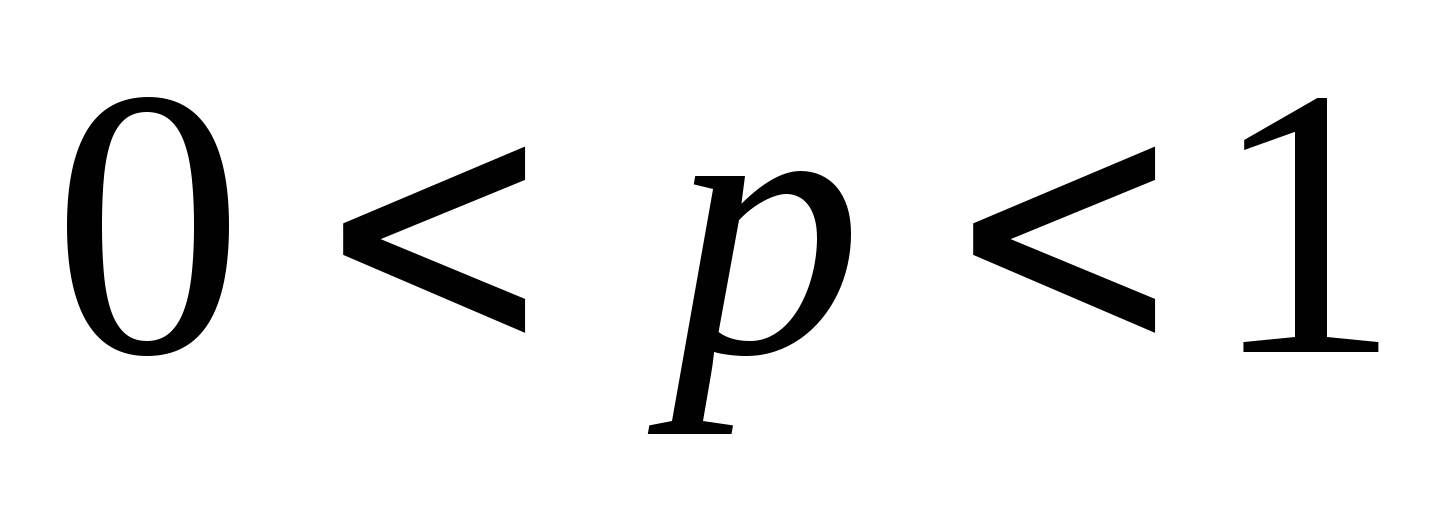 ,则称 ,则称 服从参数为 服从参数为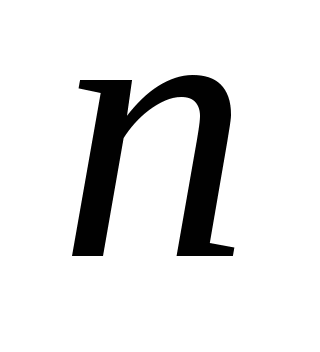 和 和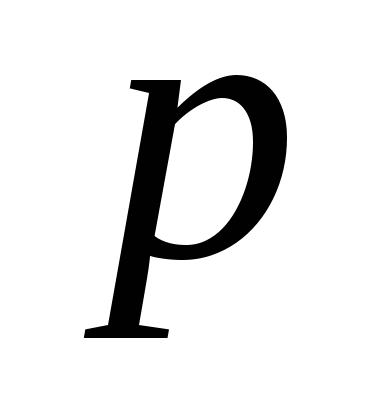 的二项分布,记作 的二项分布,记作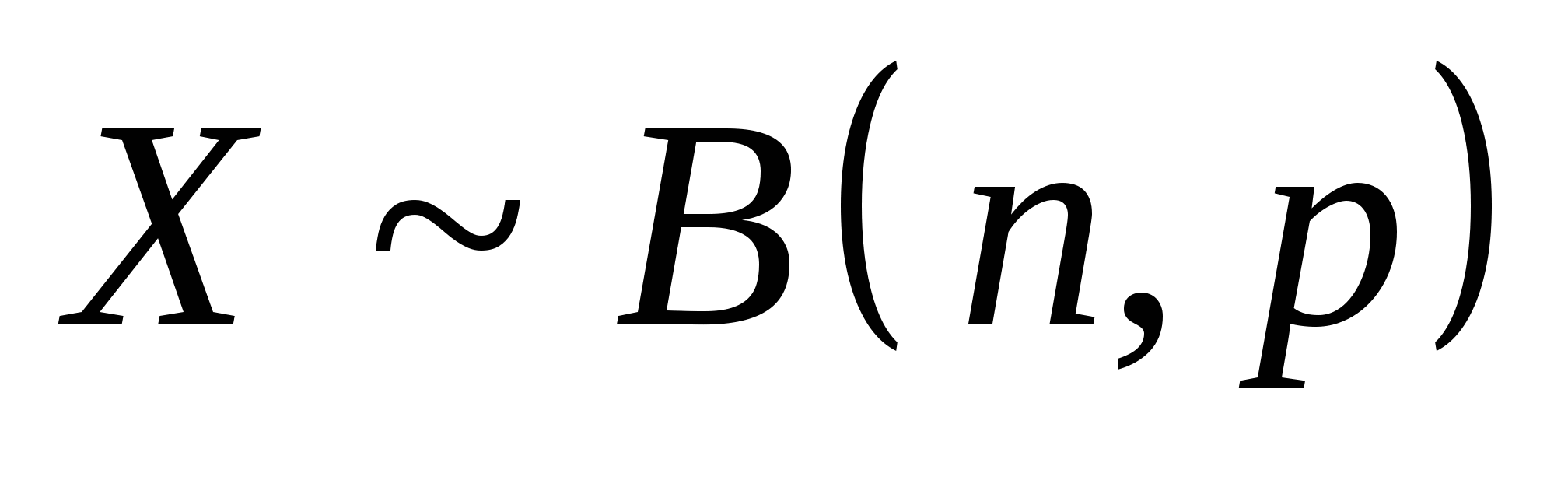 . . 例3在装有10个球的盒子中,有2个红球,从中每次取一个球,有放回地取三次,所取到红球个数 服从二项分布,其中 服从二项分布,其中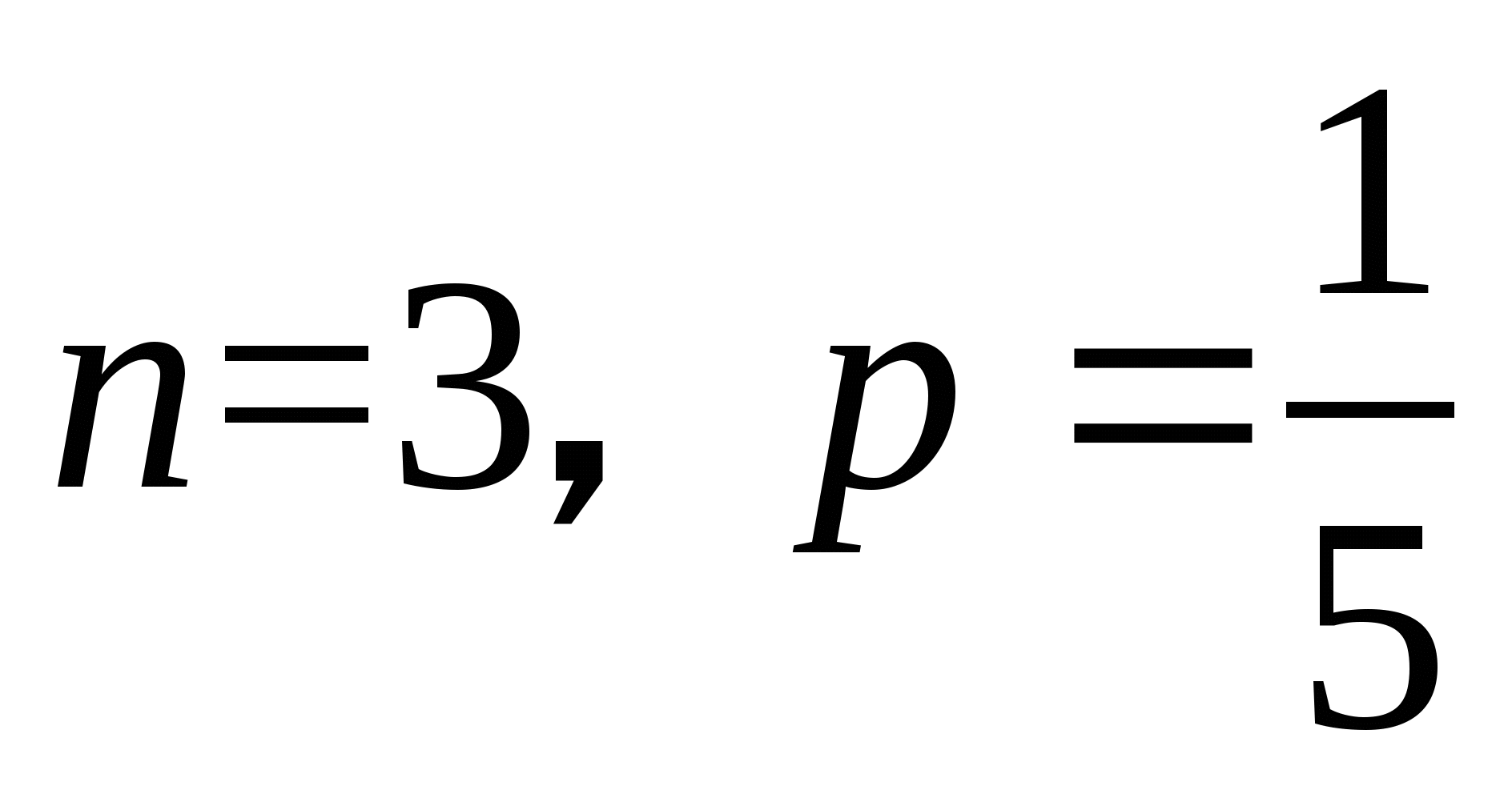 ,即 ,即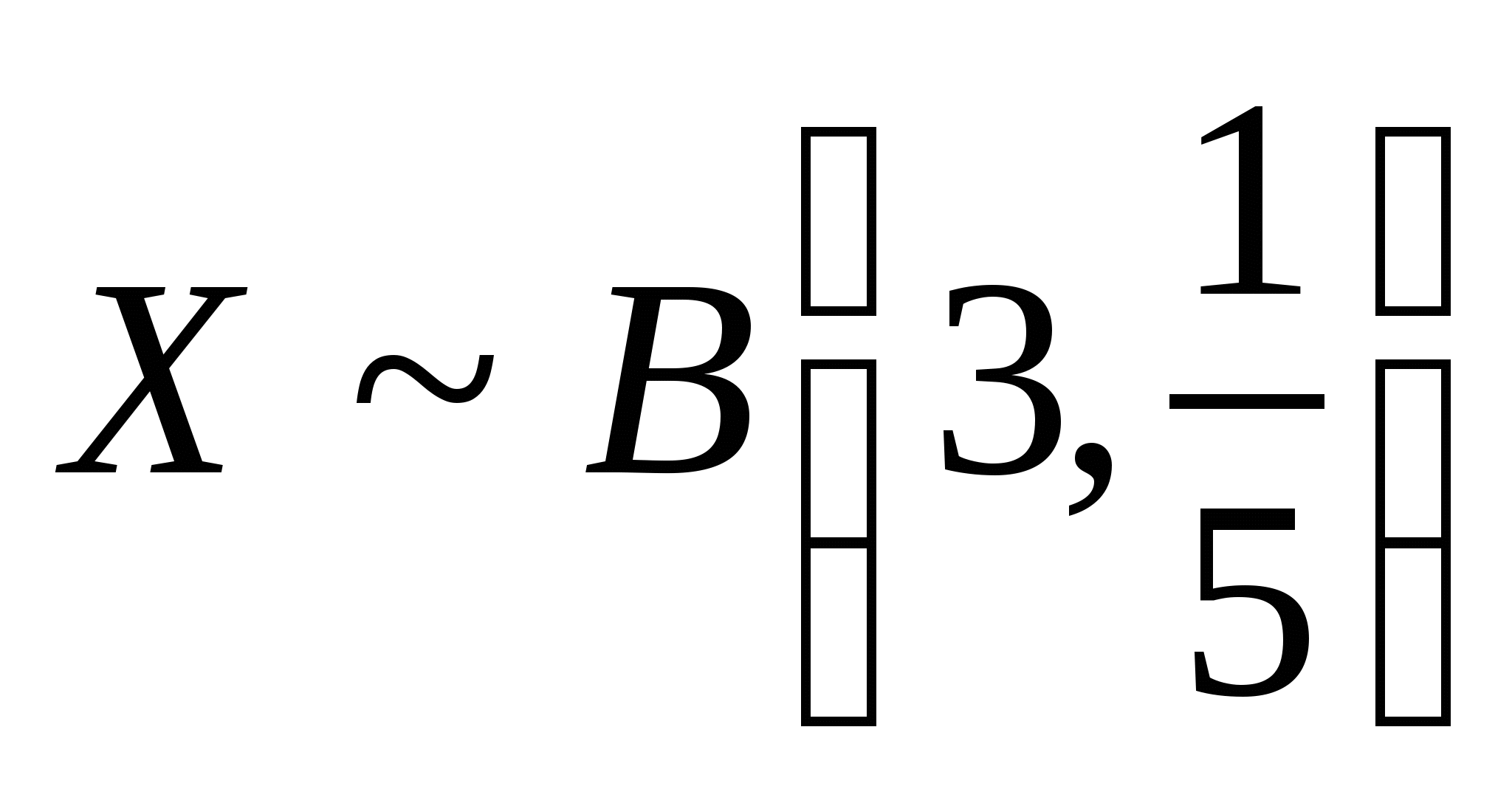 例4 从次品率为10%的一大批产品中,任取5件.(1)求5件中含有次品数 的分布律;(2)求5件中至少有4件次品的概率. 的分布律;(2)求5件中至少有4件次品的概率. 3.泊松分布 若随机变量 的分布律为 的分布律为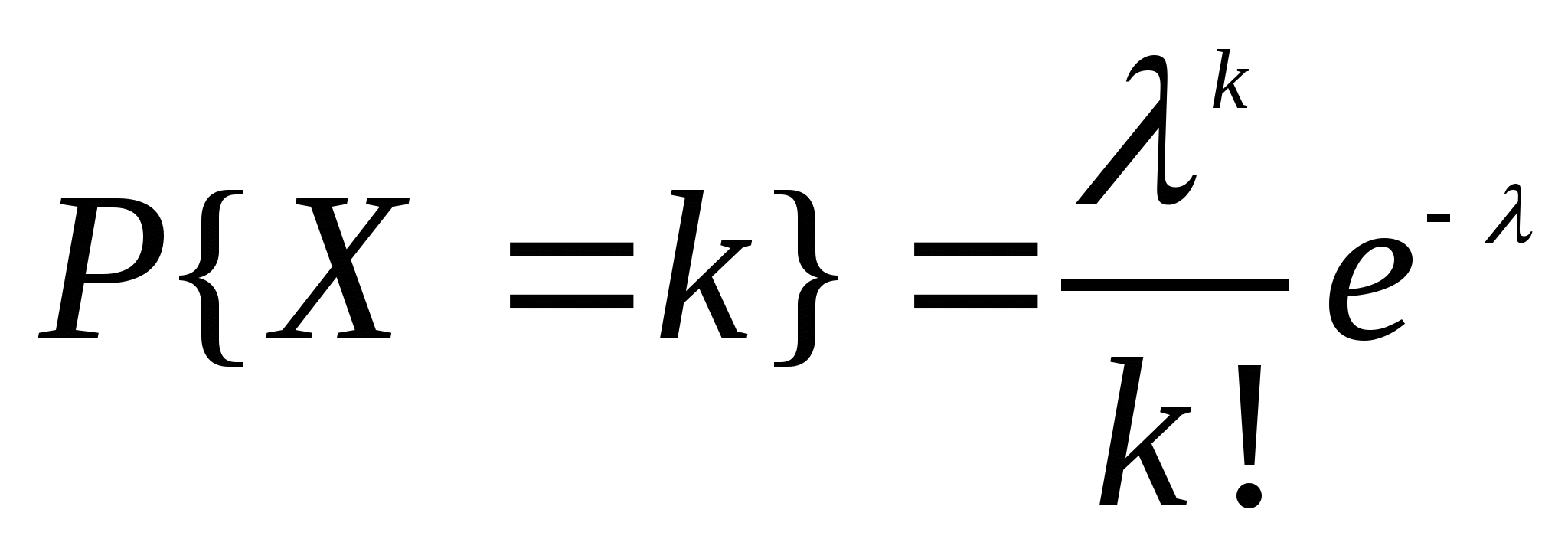 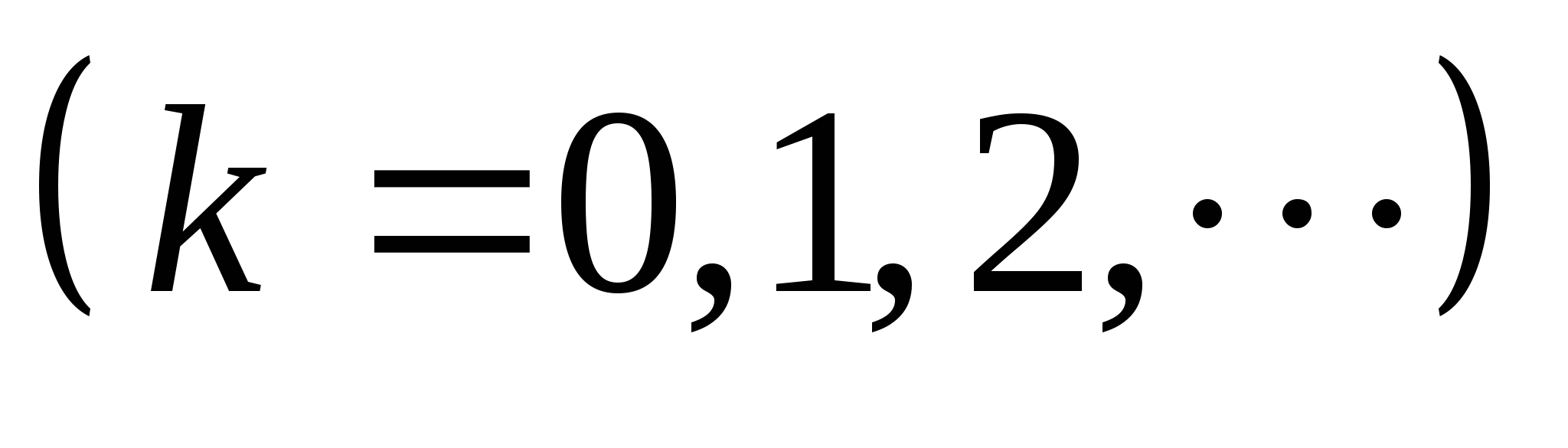 其中常数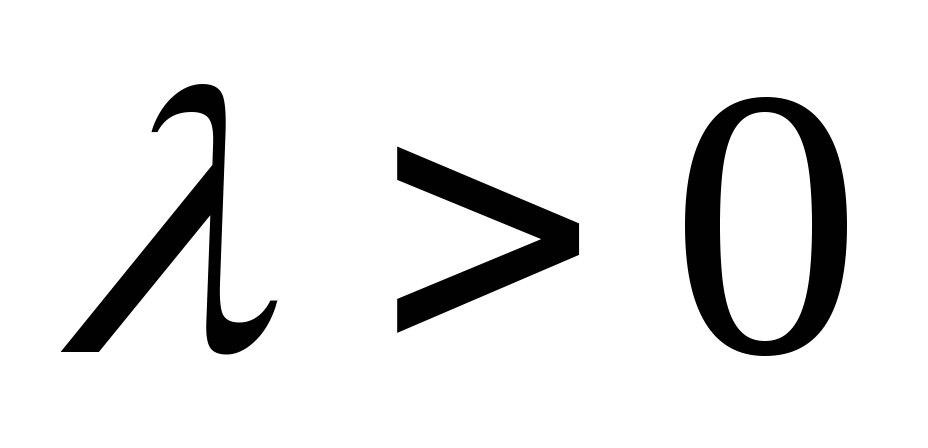 ,则称 ,则称 服从参数为 服从参数为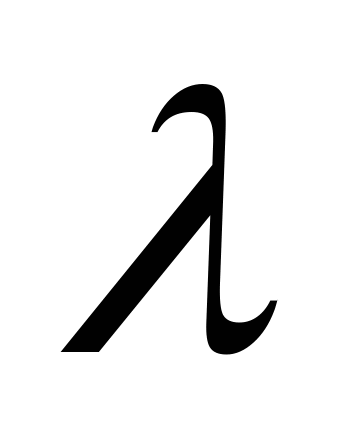 的泊松分布,记作 的泊松分布,记作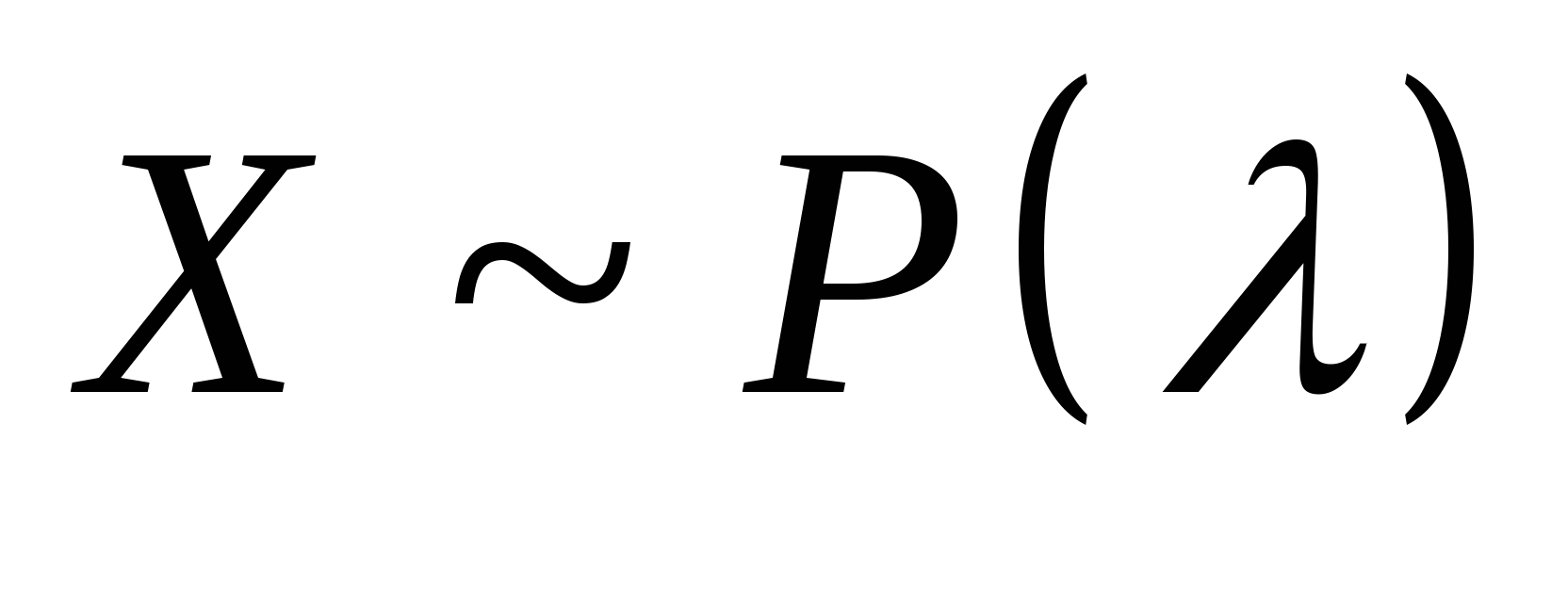 . . 例5 一电话交换台每分钟的呼唤次数 服从参数为 服从参数为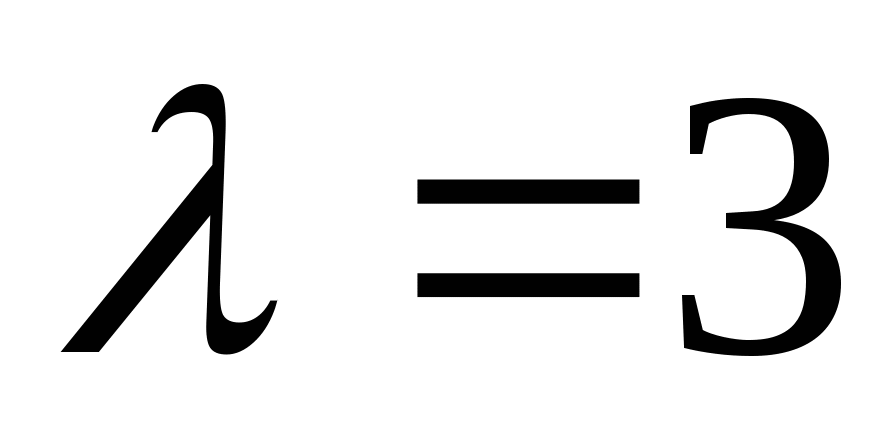 的泊松分布.求(1)每分钟至少有2次呼唤的概率;(2)每分钟恰有2次呼唤的概率. 的泊松分布.求(1)每分钟至少有2次呼唤的概率;(2)每分钟恰有2次呼唤的概率. 三、分布函数 定义2设 是随机变量,对任意实数 是随机变量,对任意实数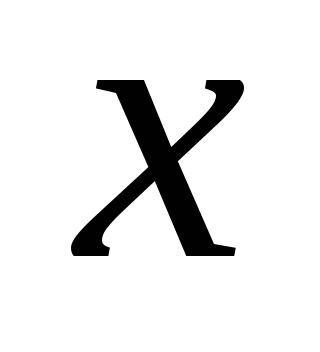 ,称函数 ,称函数  
为随机变量 的分布函数. 的分布函数. 由定义知,对于任意实数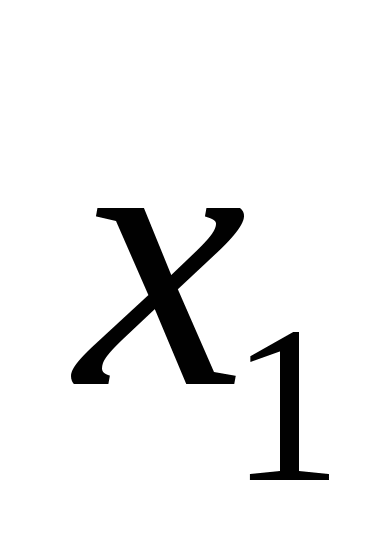 、 、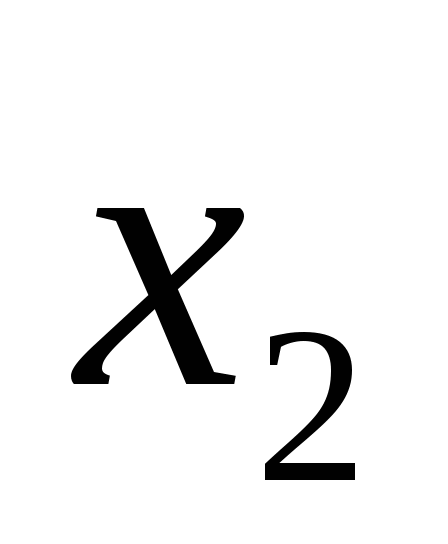 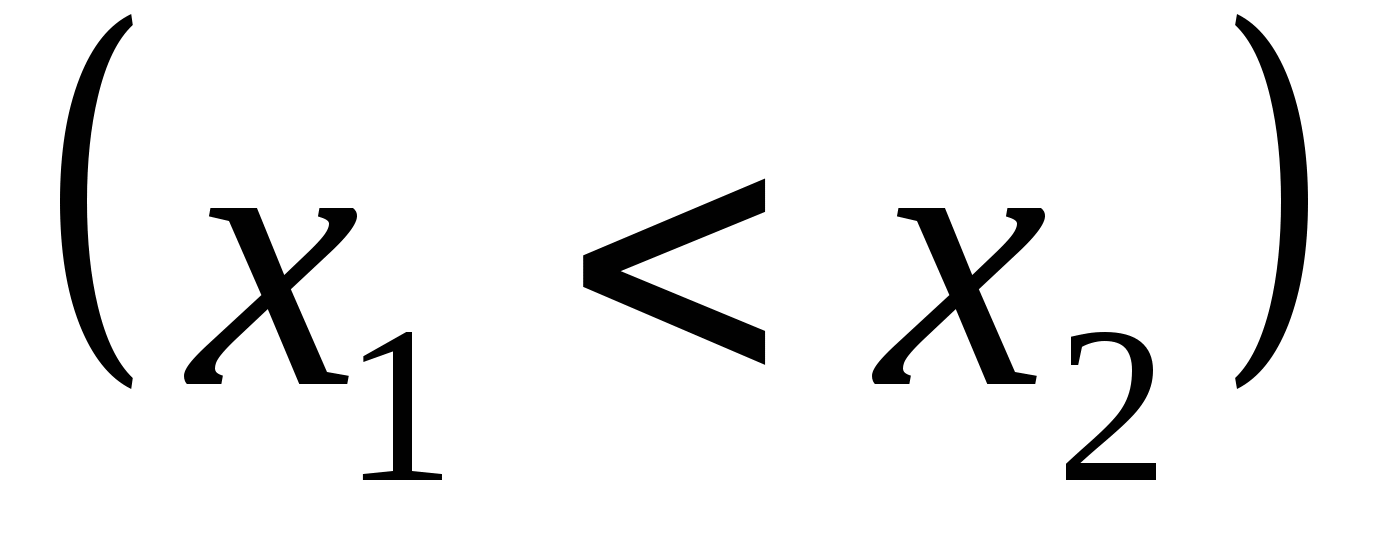 ,随机变量 ,随机变量 落在区间( 落在区间(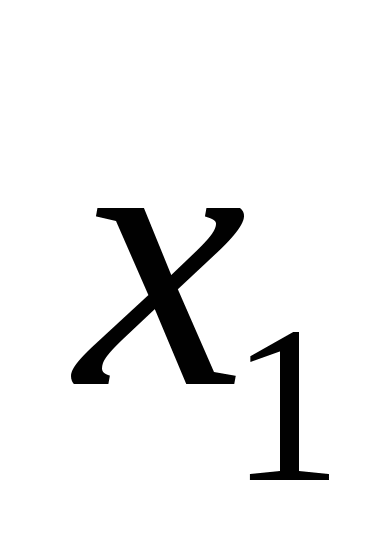 , ,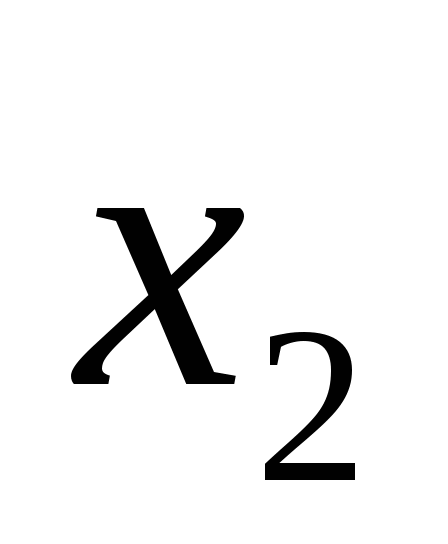 ]内的概率为 ]内的概率为 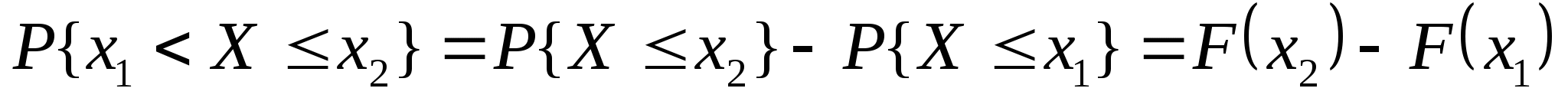
因此,当已知 的分布函数时, 的分布函数时, 落在区间( 落在区间(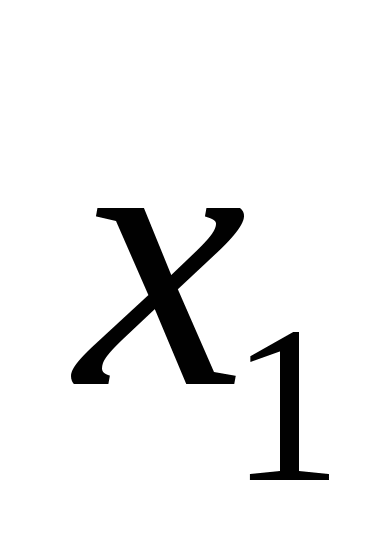 , ,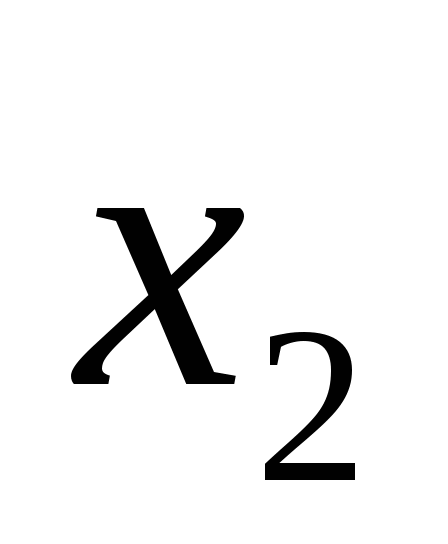 ]内的概率就是其在该区间函数值的增量.这表明分布函数完整地描述了随机变量的统计规律性. ]内的概率就是其在该区间函数值的增量.这表明分布函数完整地描述了随机变量的统计规律性. 分布函数具有以下性质: (1)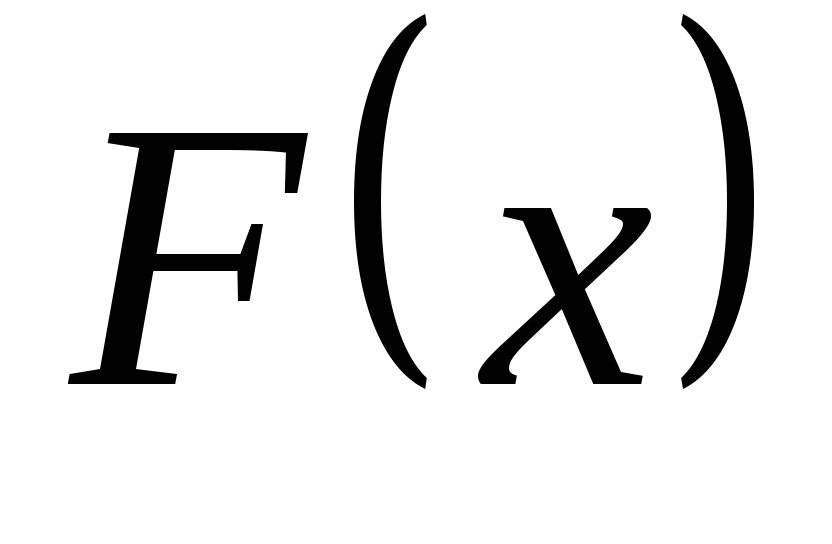 是一个不减函数,即当 是一个不减函数,即当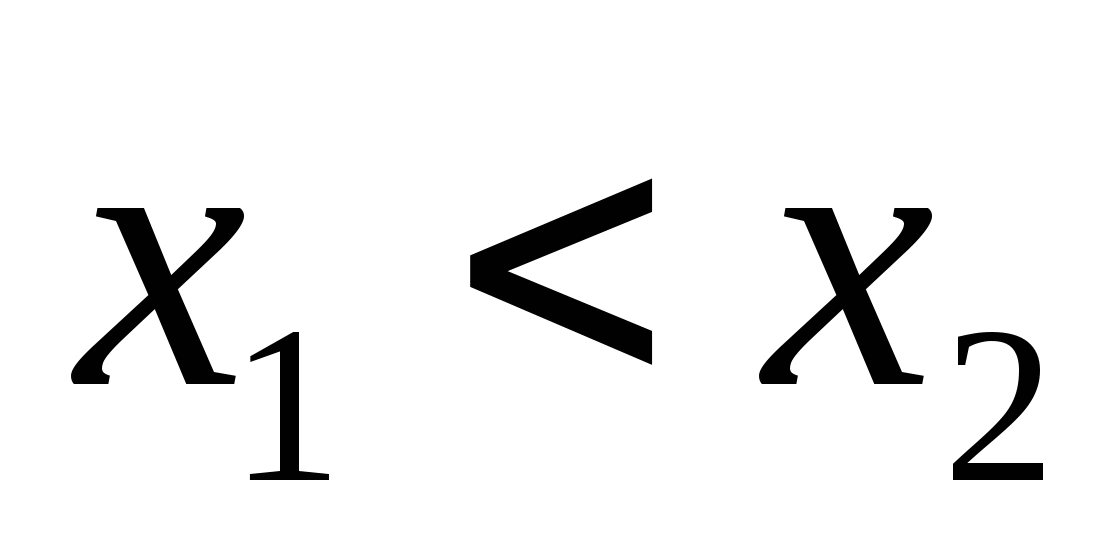 时有 时有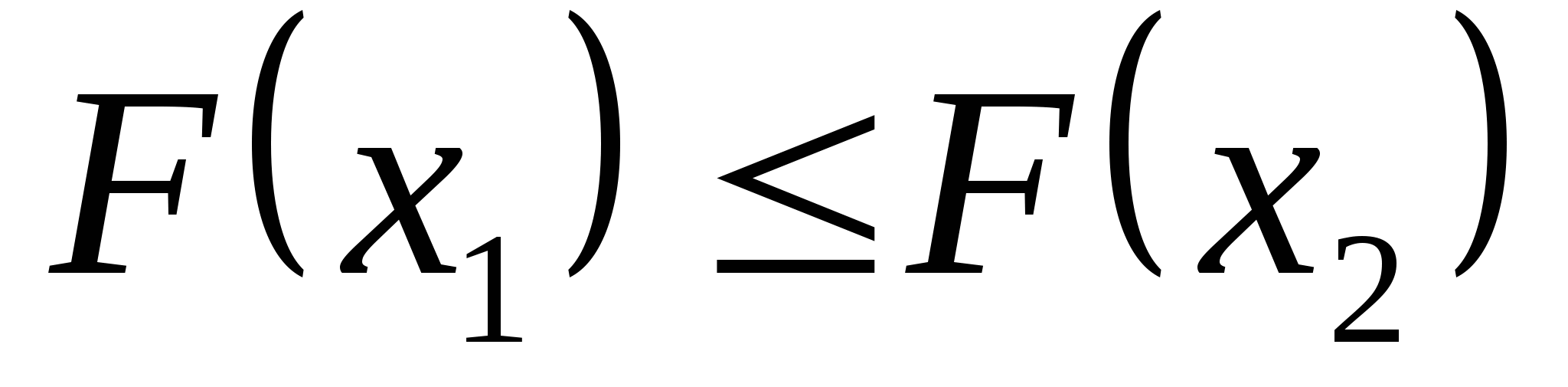 ; ; (2)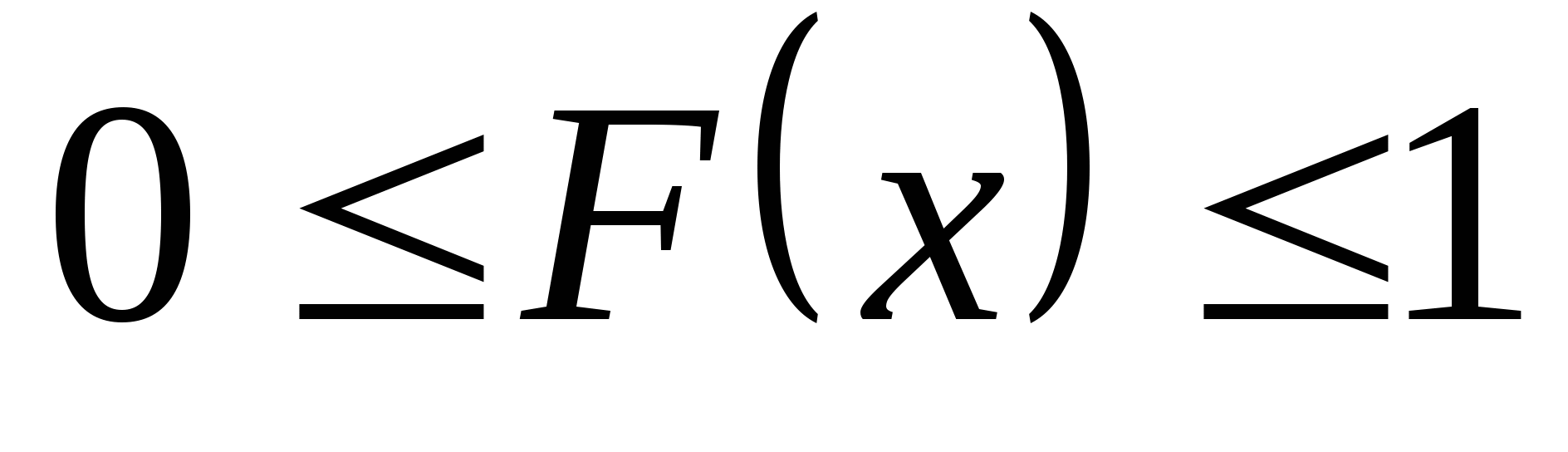 ; ; (3) , ,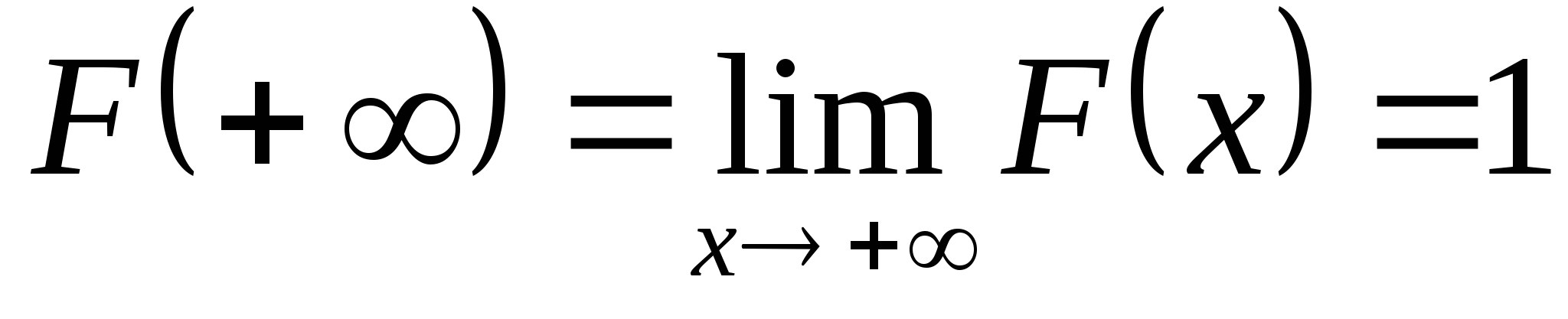 ; ; (4)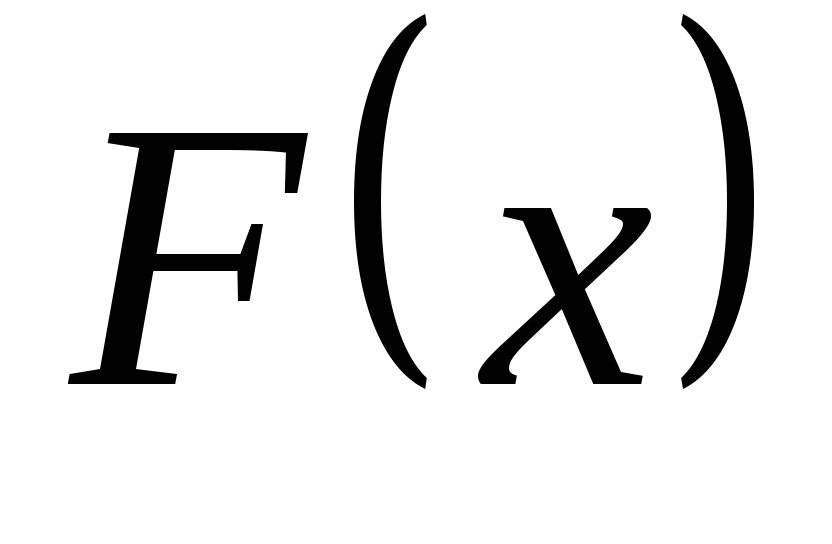 是右连续的. 是右连续的. 证明略. 分布函数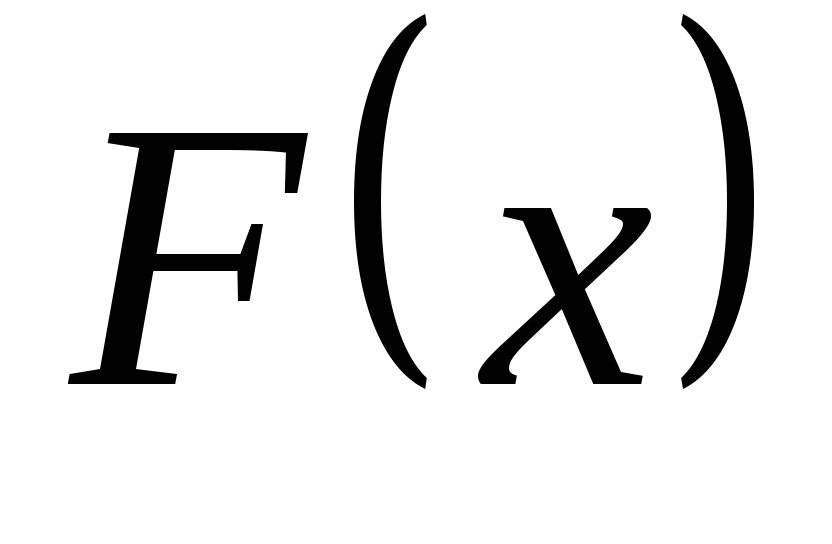 是事件 是事件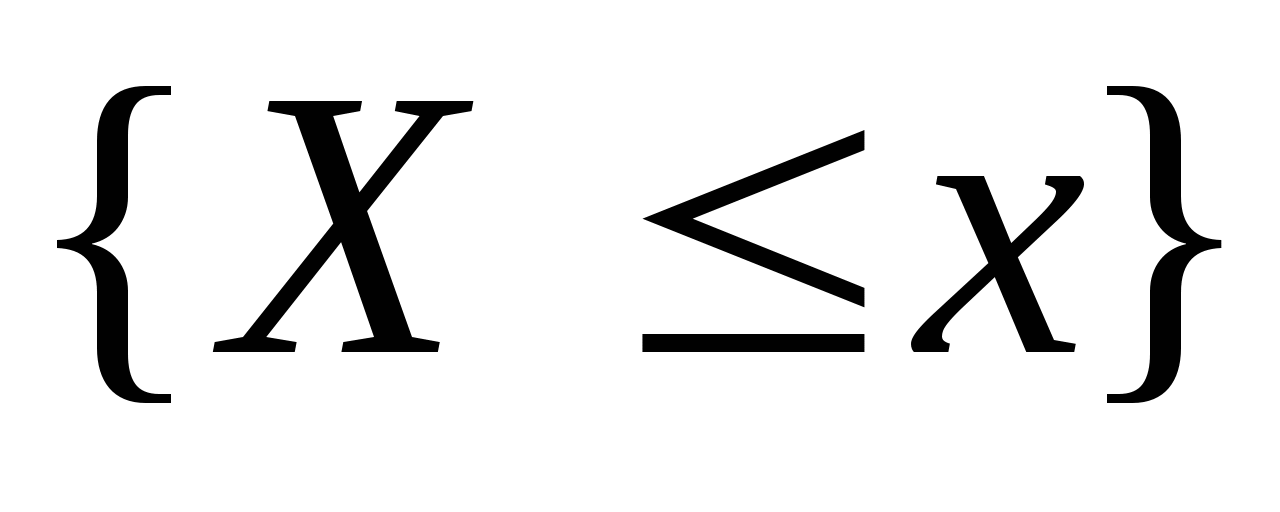 的概率.因此,求随机变量的分布函数的方法是求概率 的概率.因此,求随机变量的分布函数的方法是求概率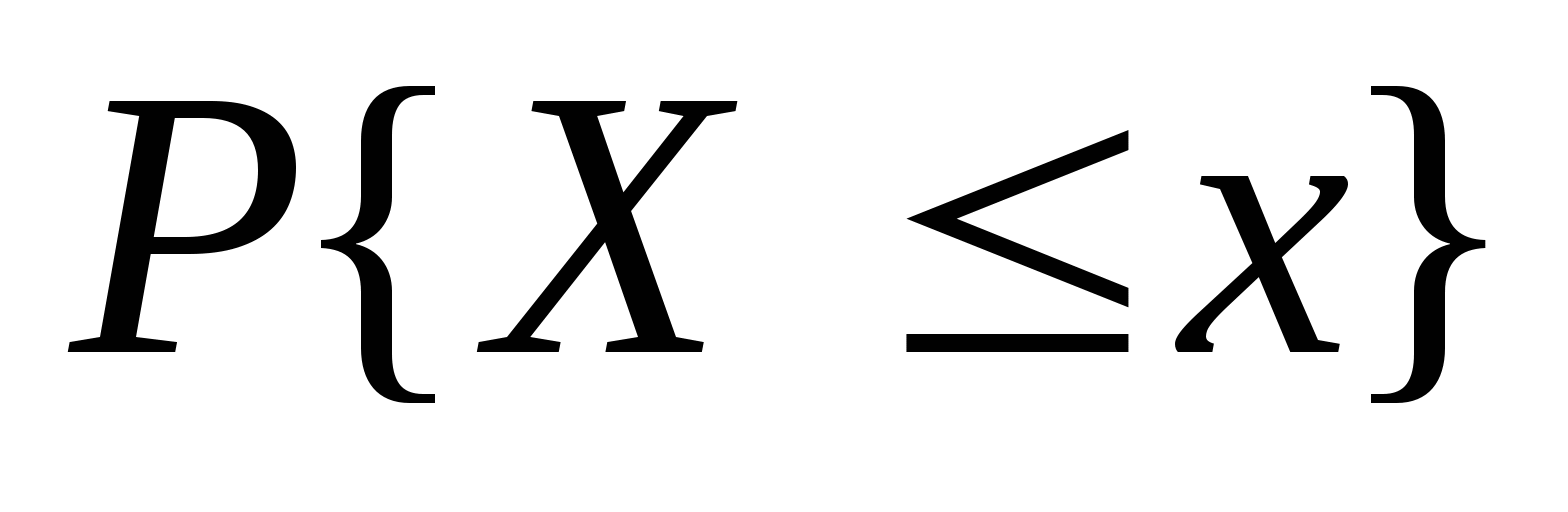 , , ,因此,若离散型随机变量的分布律为 ,因此,若离散型随机变量的分布律为 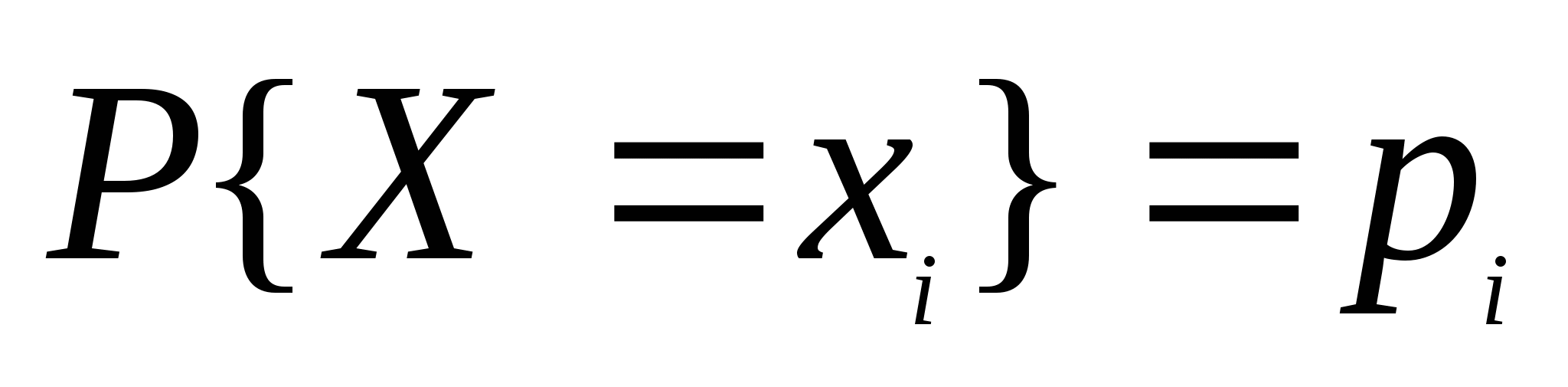 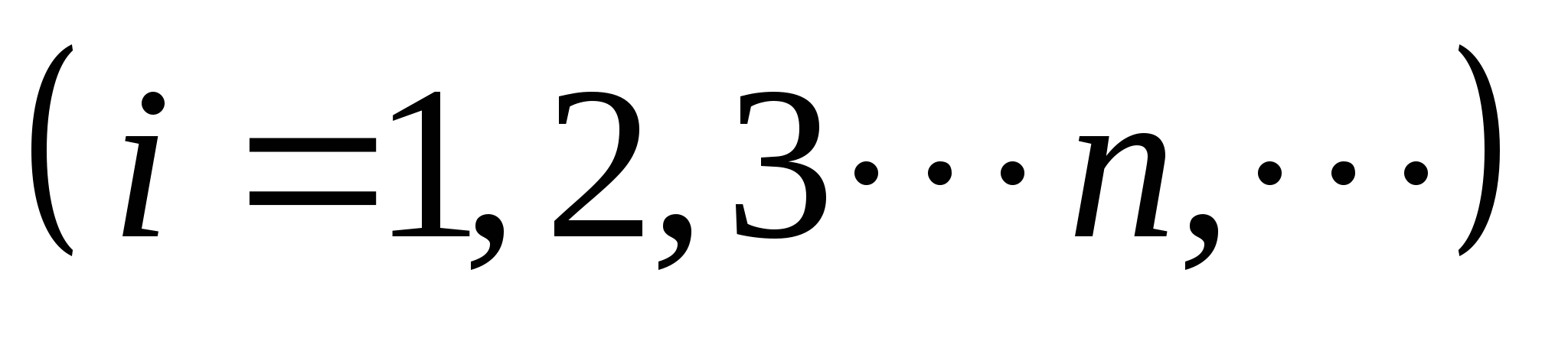 , ,
则其分布函数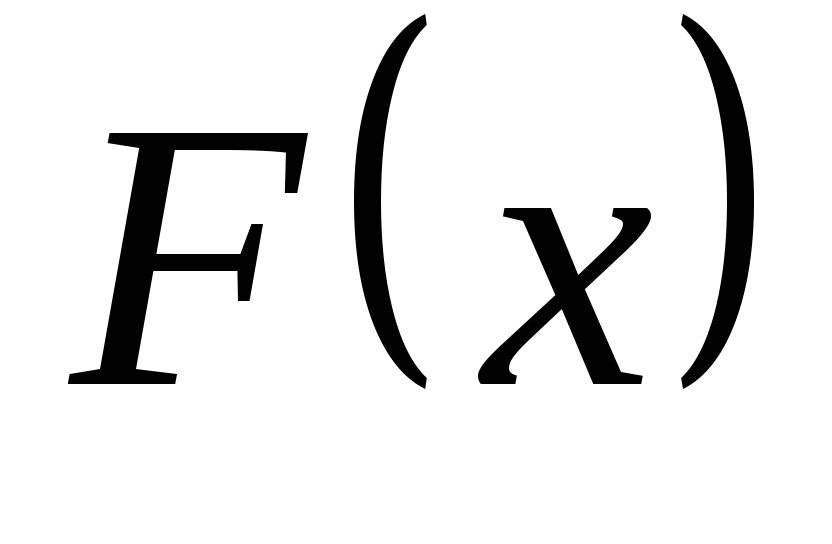 = = 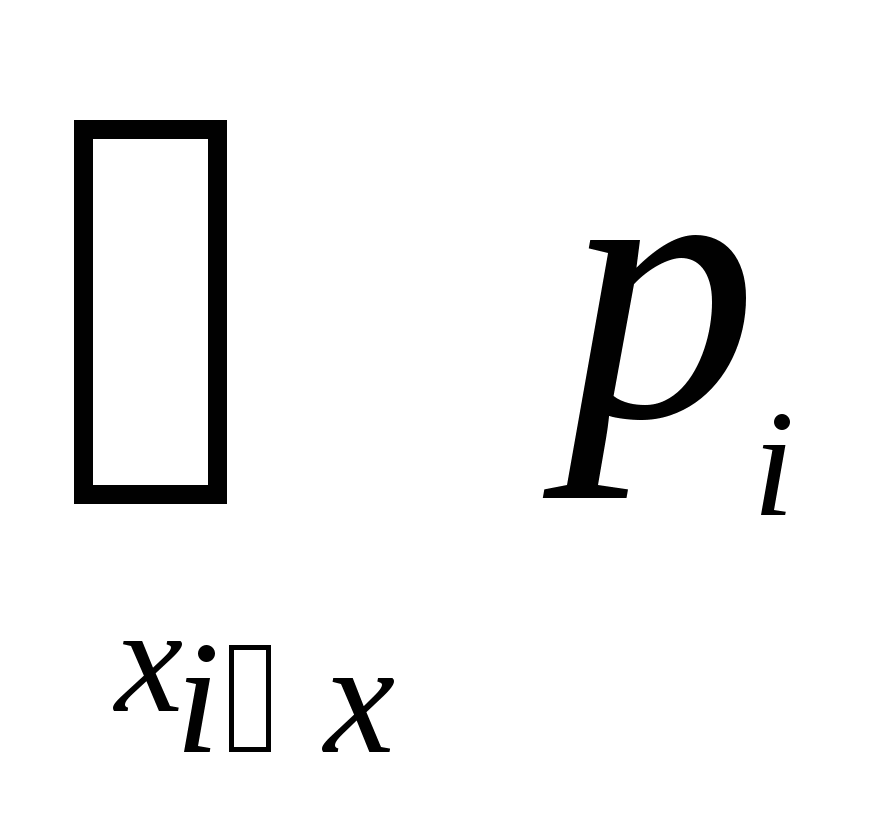 . . 例7 设随机变量 的分布律为 的分布律为   -1 1 2 -1 1 2
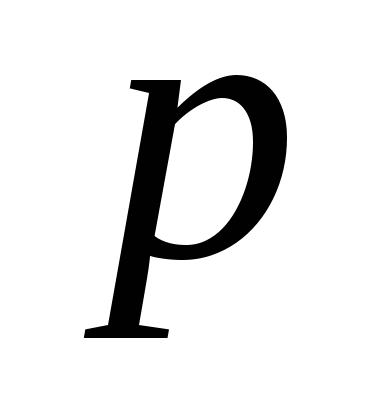  0.3 0.2 0.5 0.3 0.2 0.5
求(1) 的分布函数 的分布函数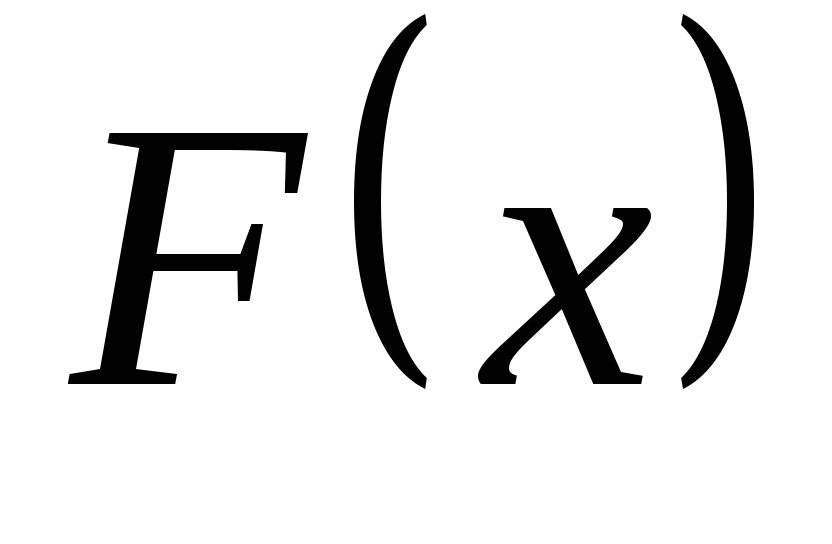 ; (2) ; (2)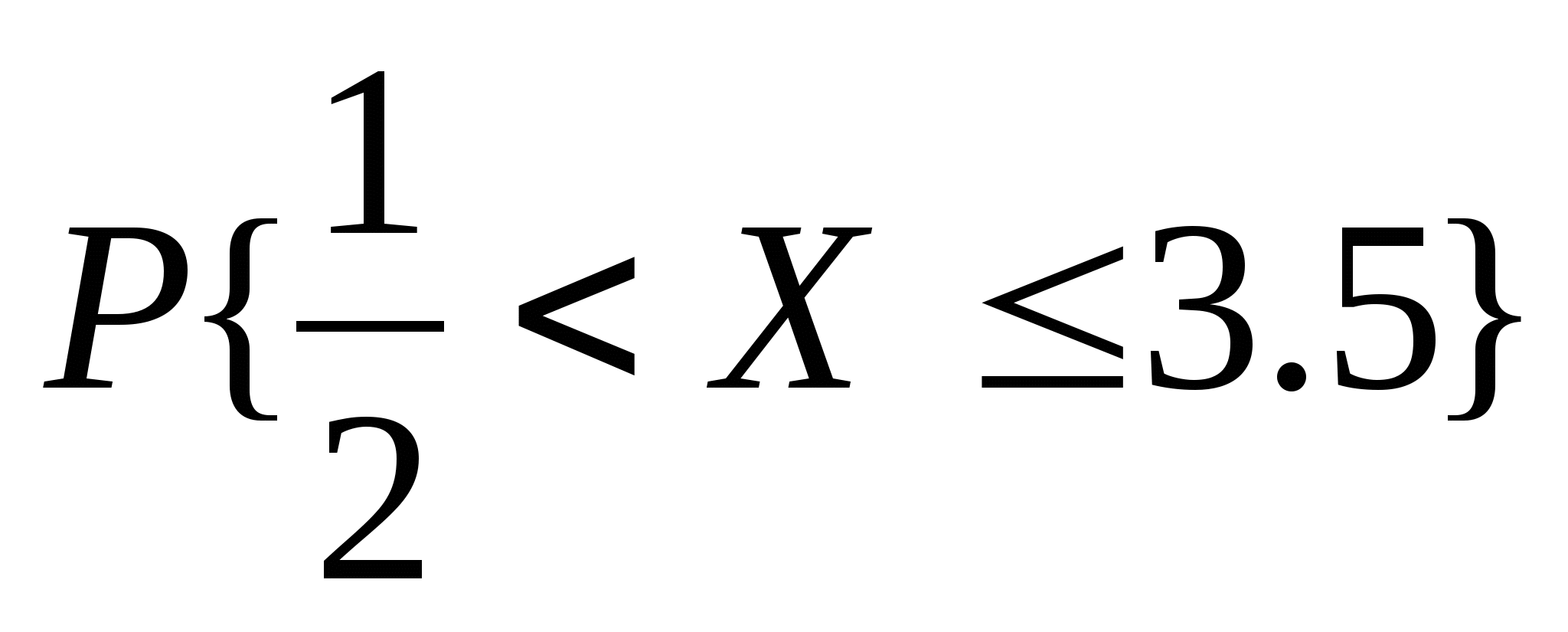 . . 第二节 连续型随机变量的分布一、连续型随机变量的分布密度 定义 设随机变量 的分布函数为 的分布函数为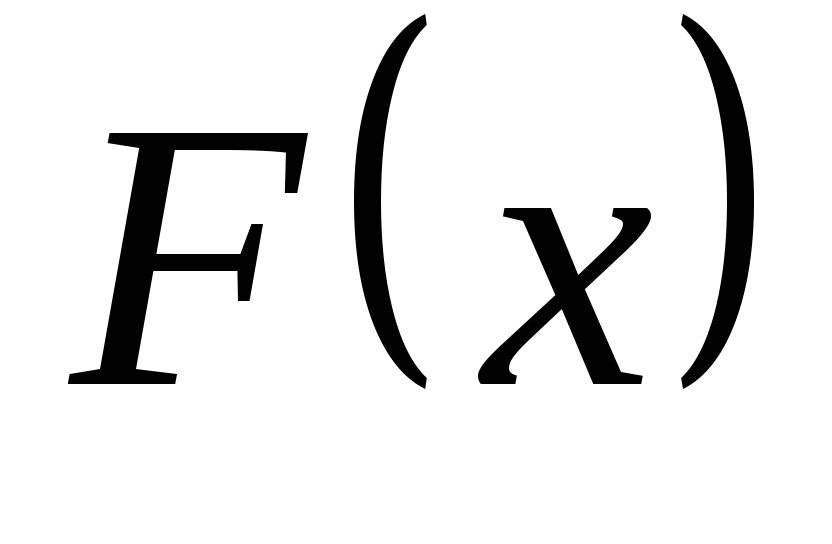 ,如果存在非负可积函数 ,如果存在非负可积函数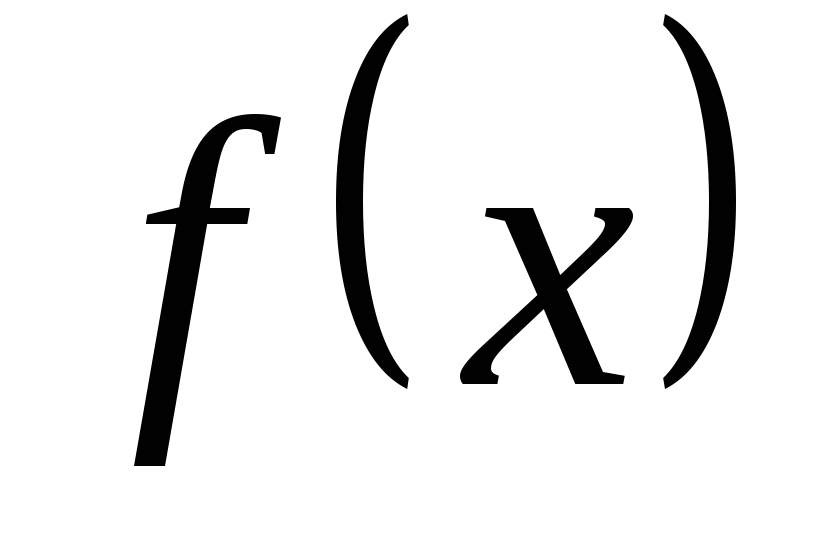 ,使得对于任意实数 ,使得对于任意实数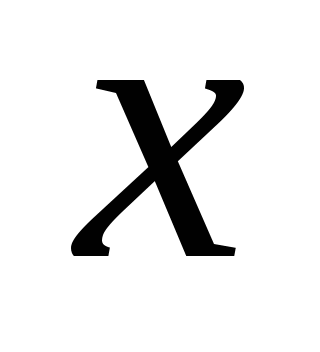 ,有 ,有 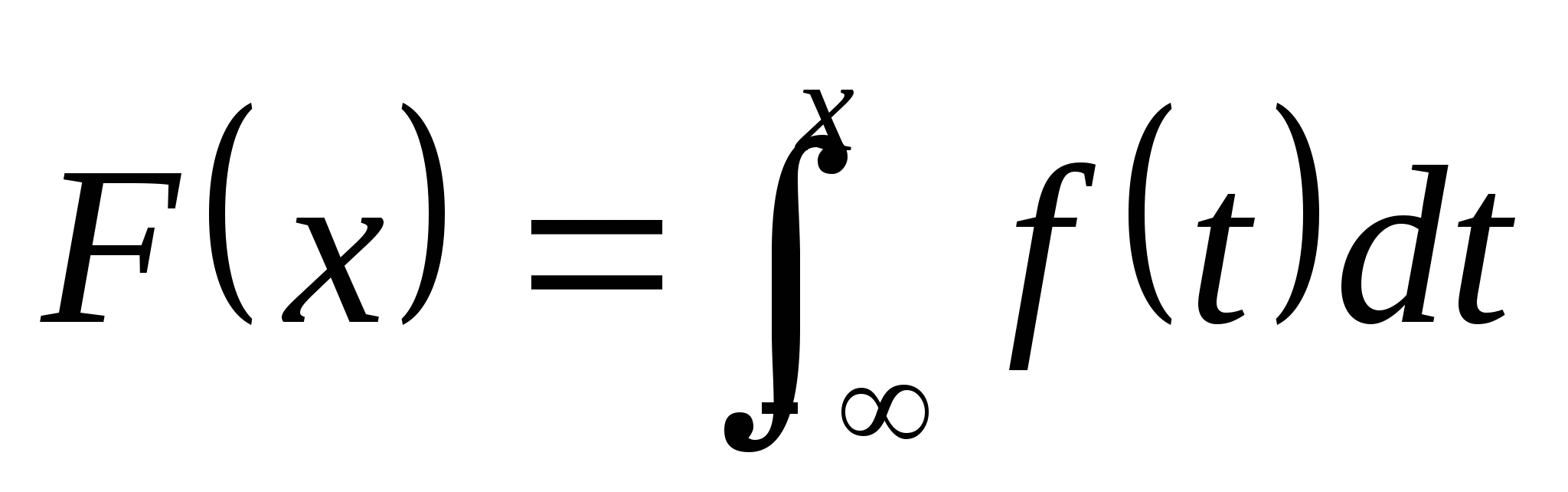 则称 为连续型随机变量,并称 为连续型随机变量,并称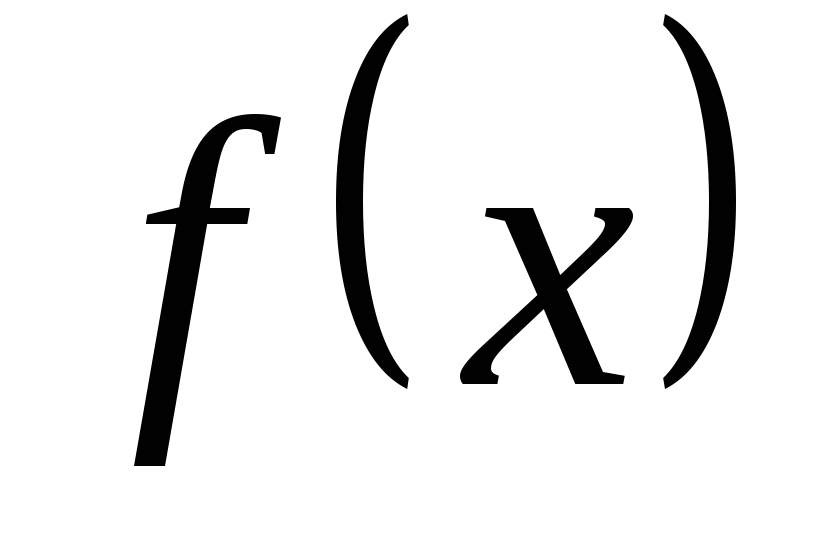 为 为 的概率密度函数或密度函数,简称概率密度或密度. 的概率密度函数或密度函数,简称概率密度或密度. 由此定义知,连续型随机变量的分布函数是连续函数.密度函数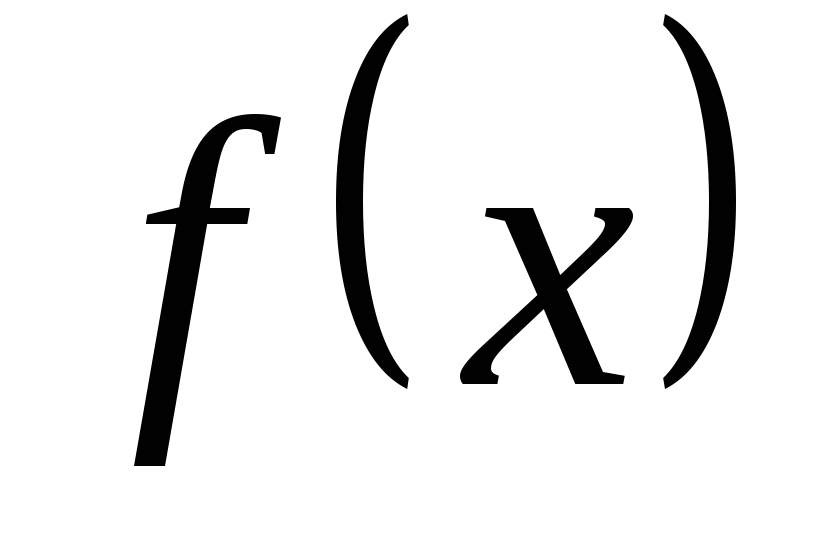 具有如下性质: 具有如下性质: (1)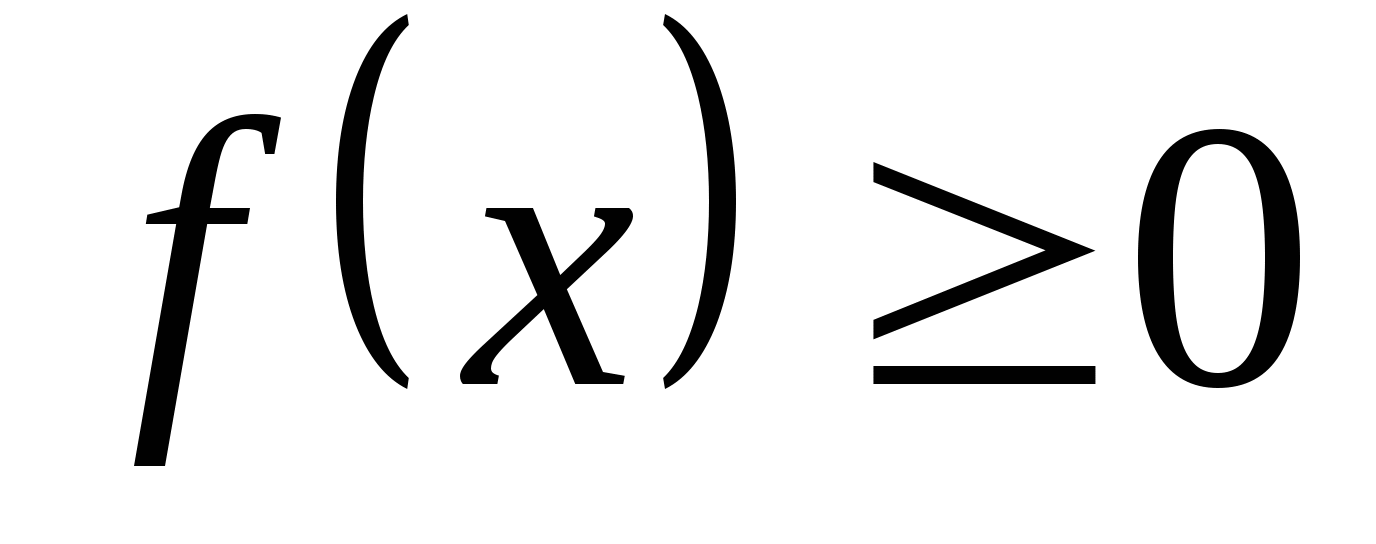 ; (2) ; (2)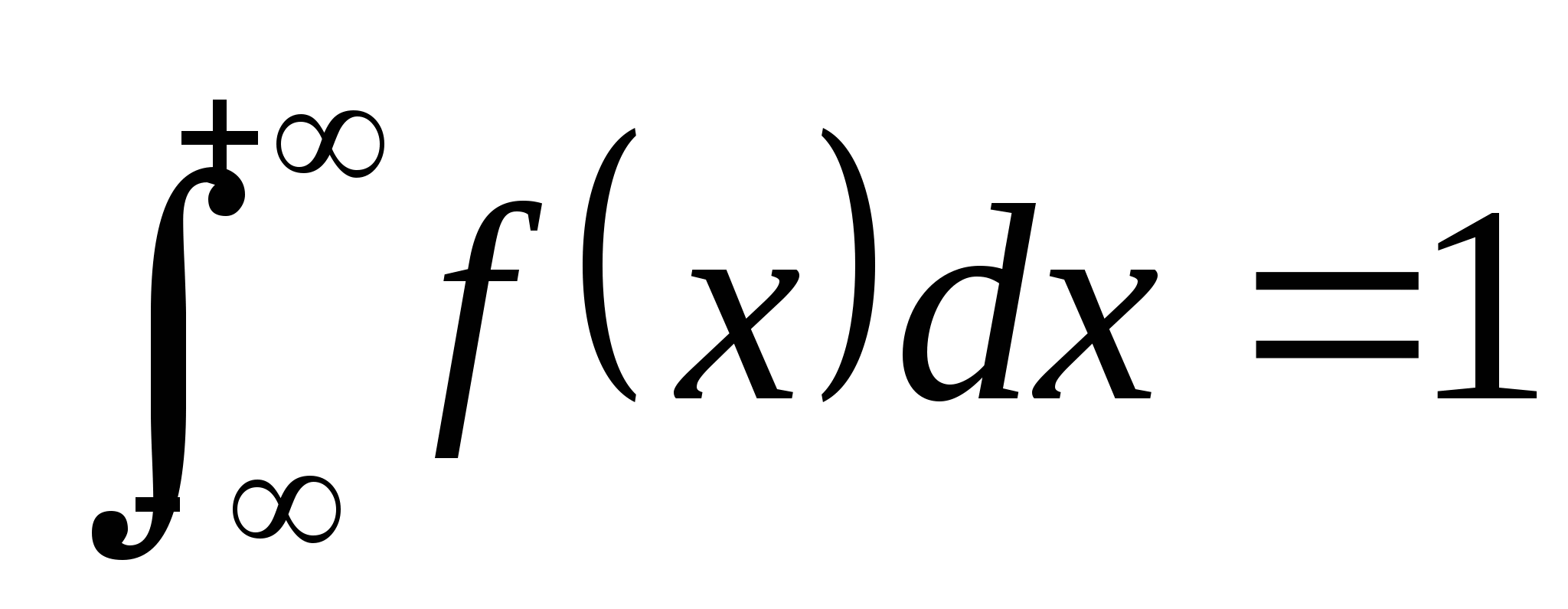 ; ; (3)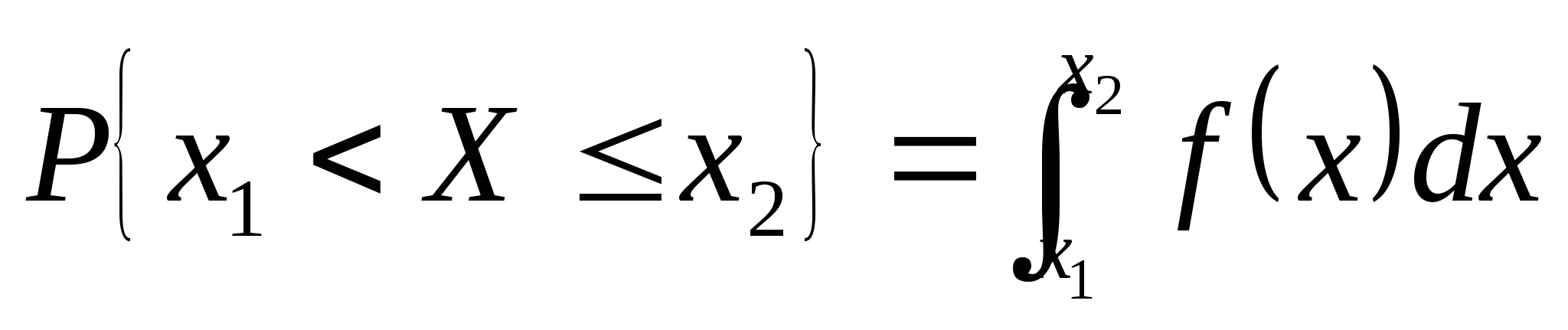  ;(4)在 ;(4)在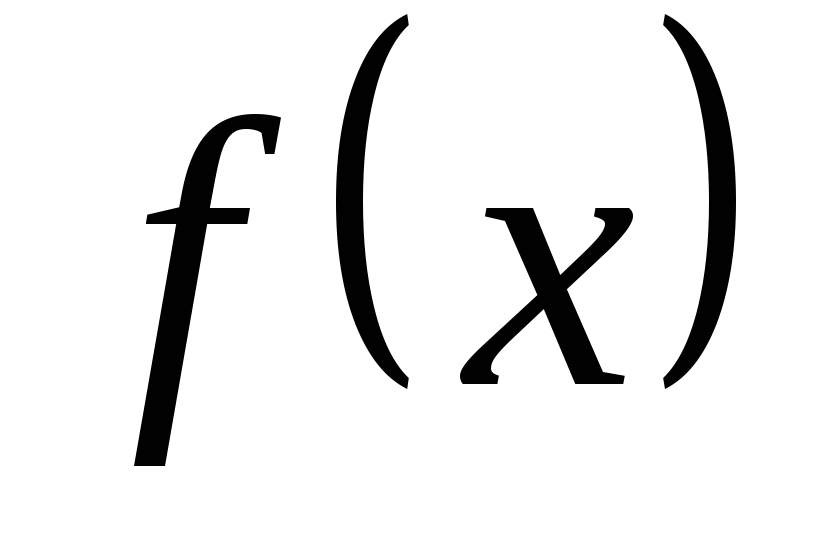 的连续点处, 的连续点处,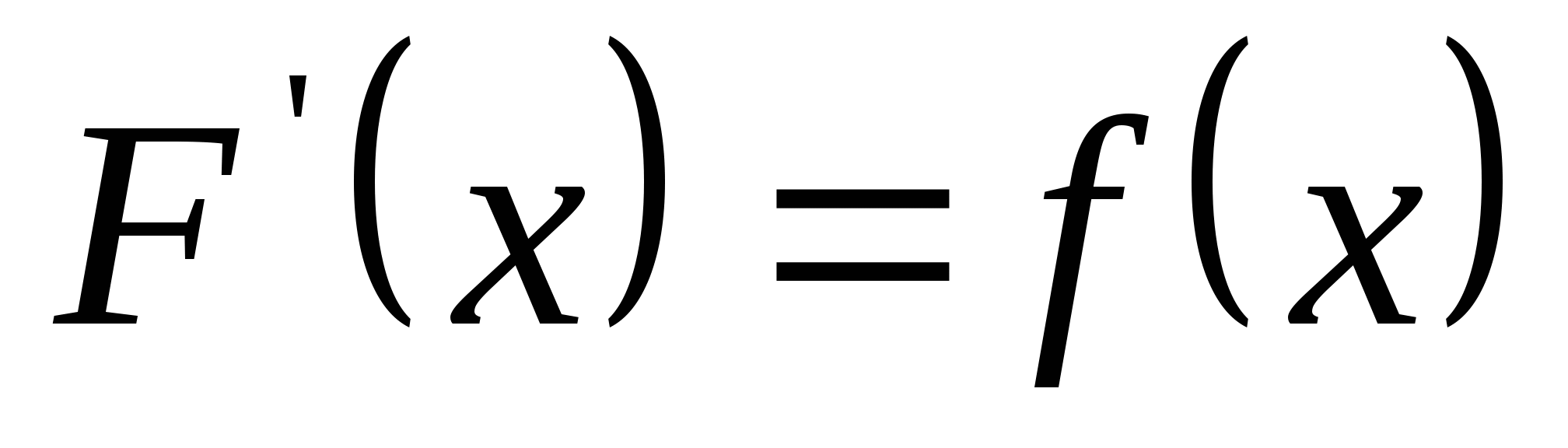 . . 例1 设随机变量 的密度函数为 的密度函数为 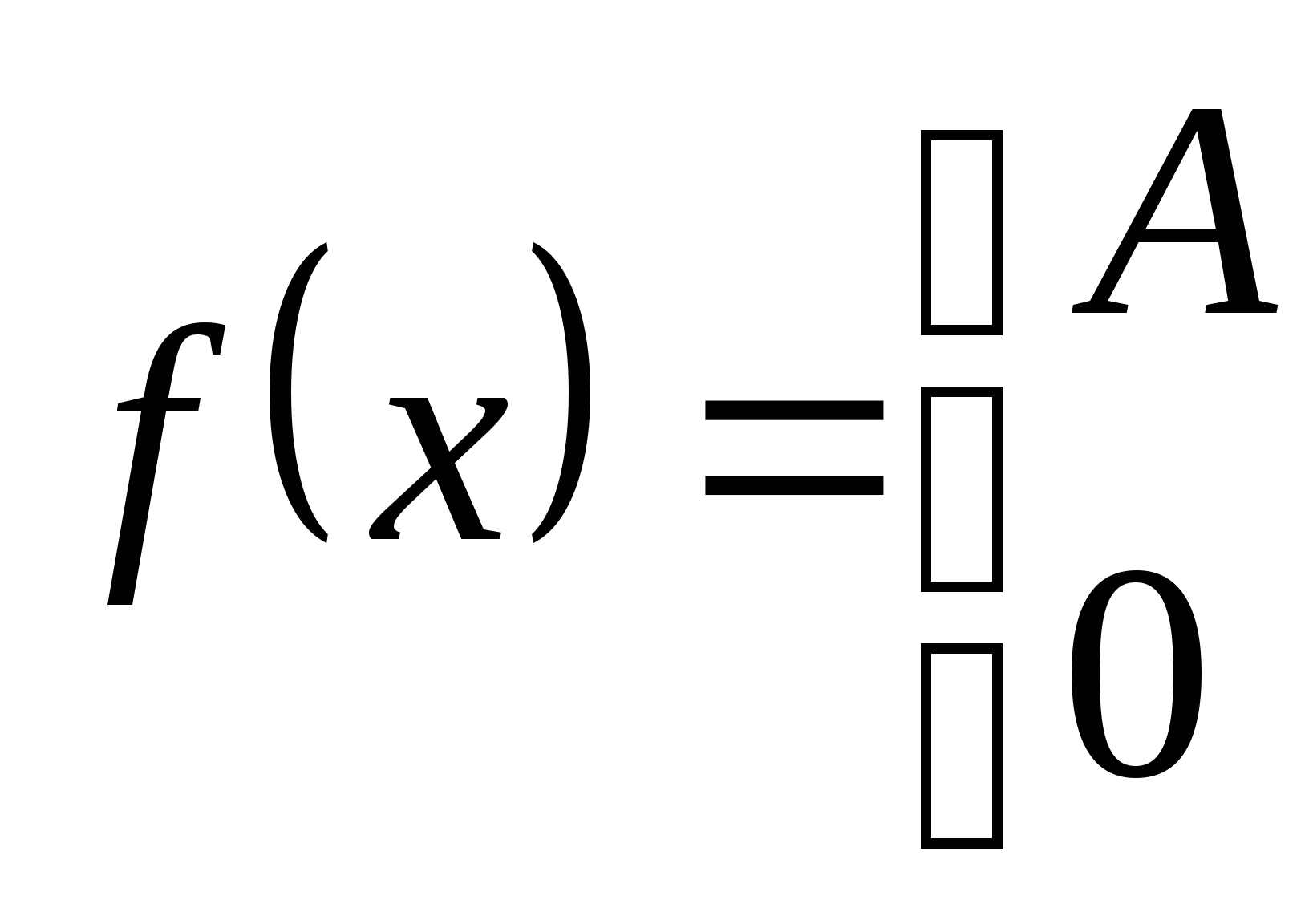 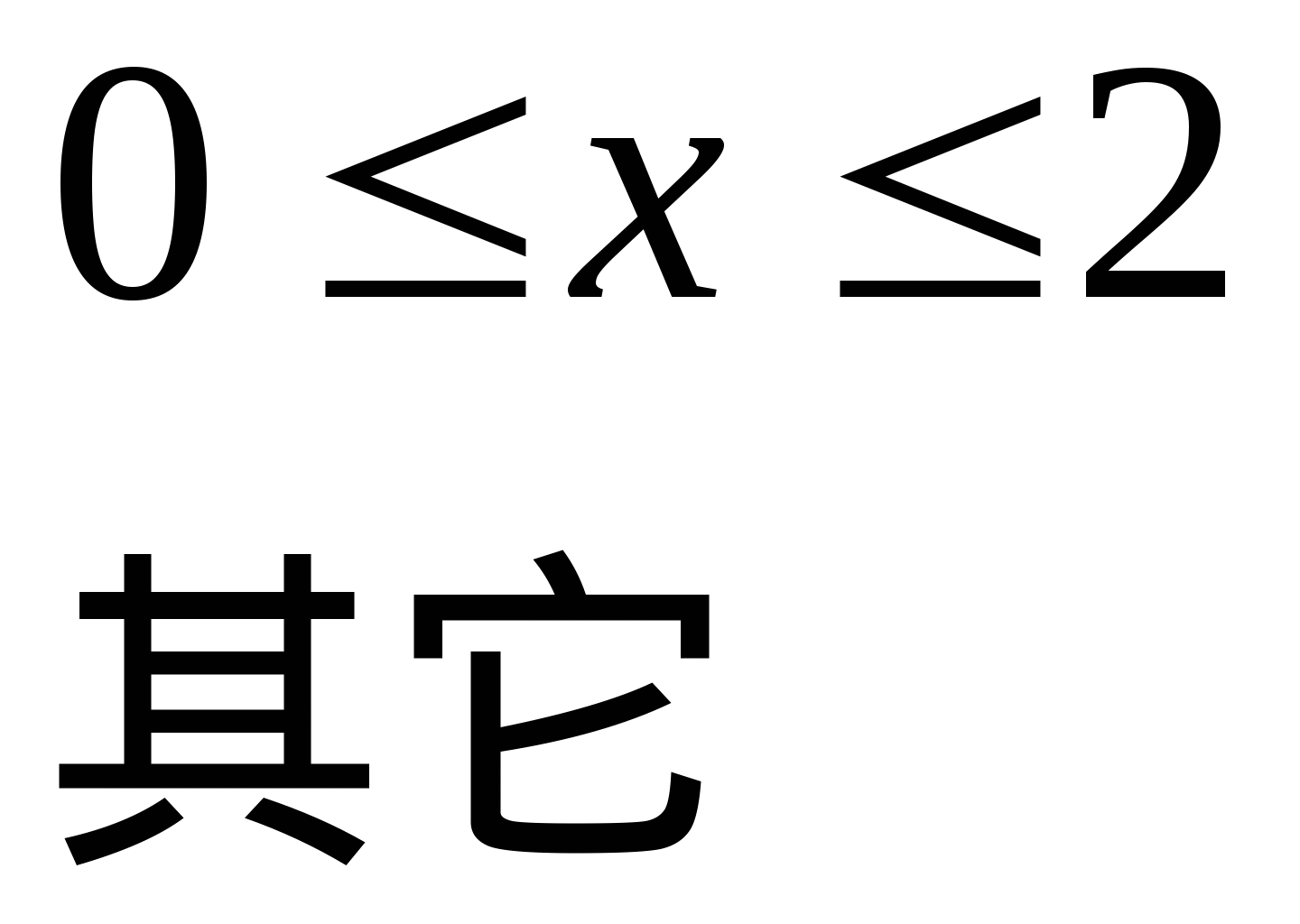 , ,
求(1)常数 ;(2) ;(2)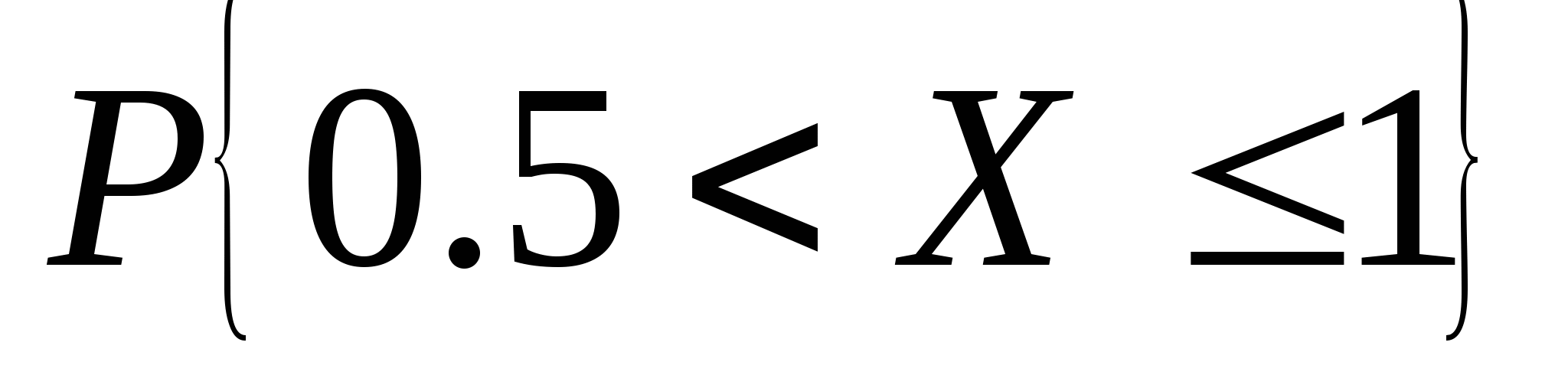 . . 例2 已知连续型随机变量 的密度函数为 的密度函数为 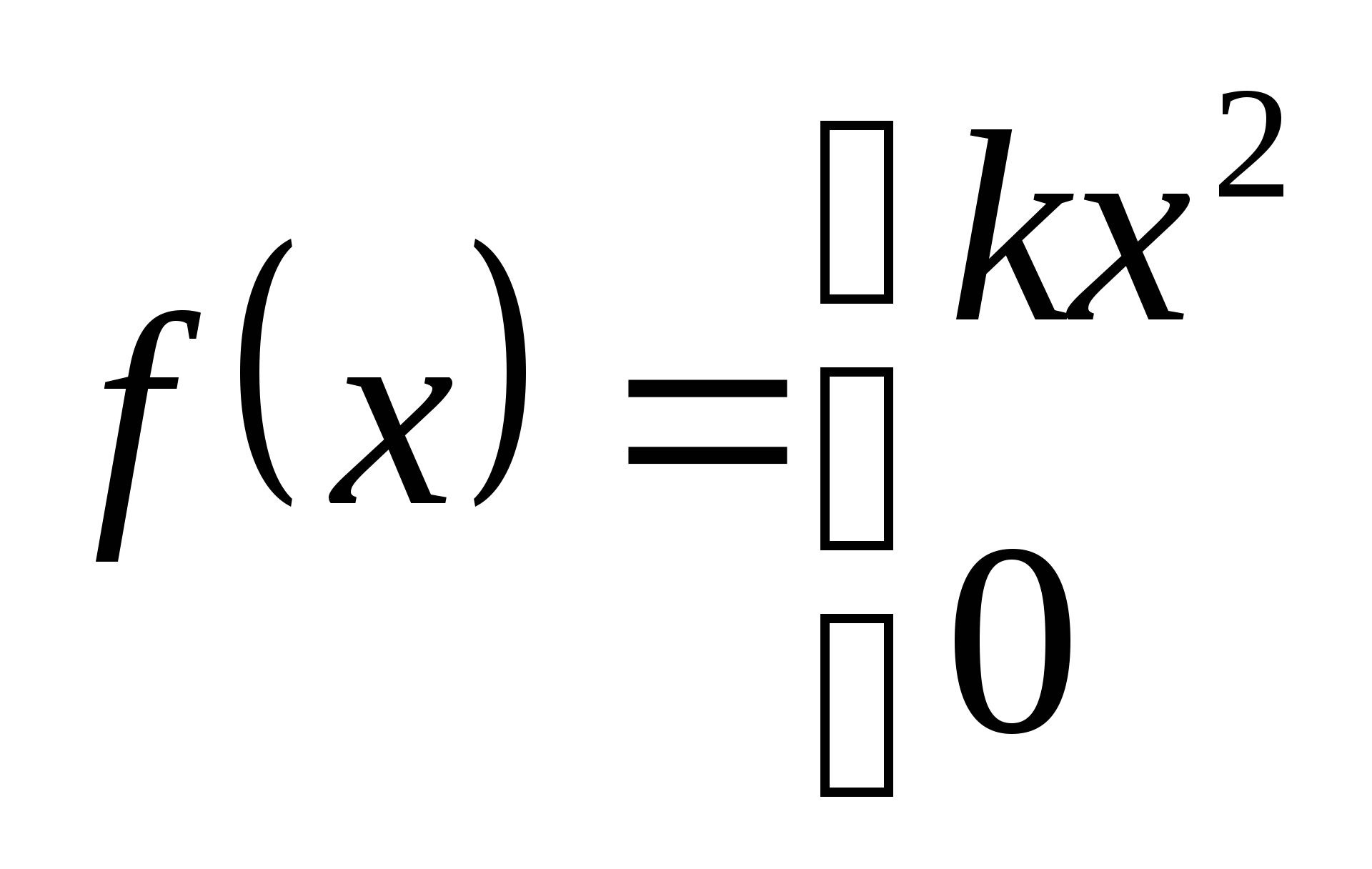 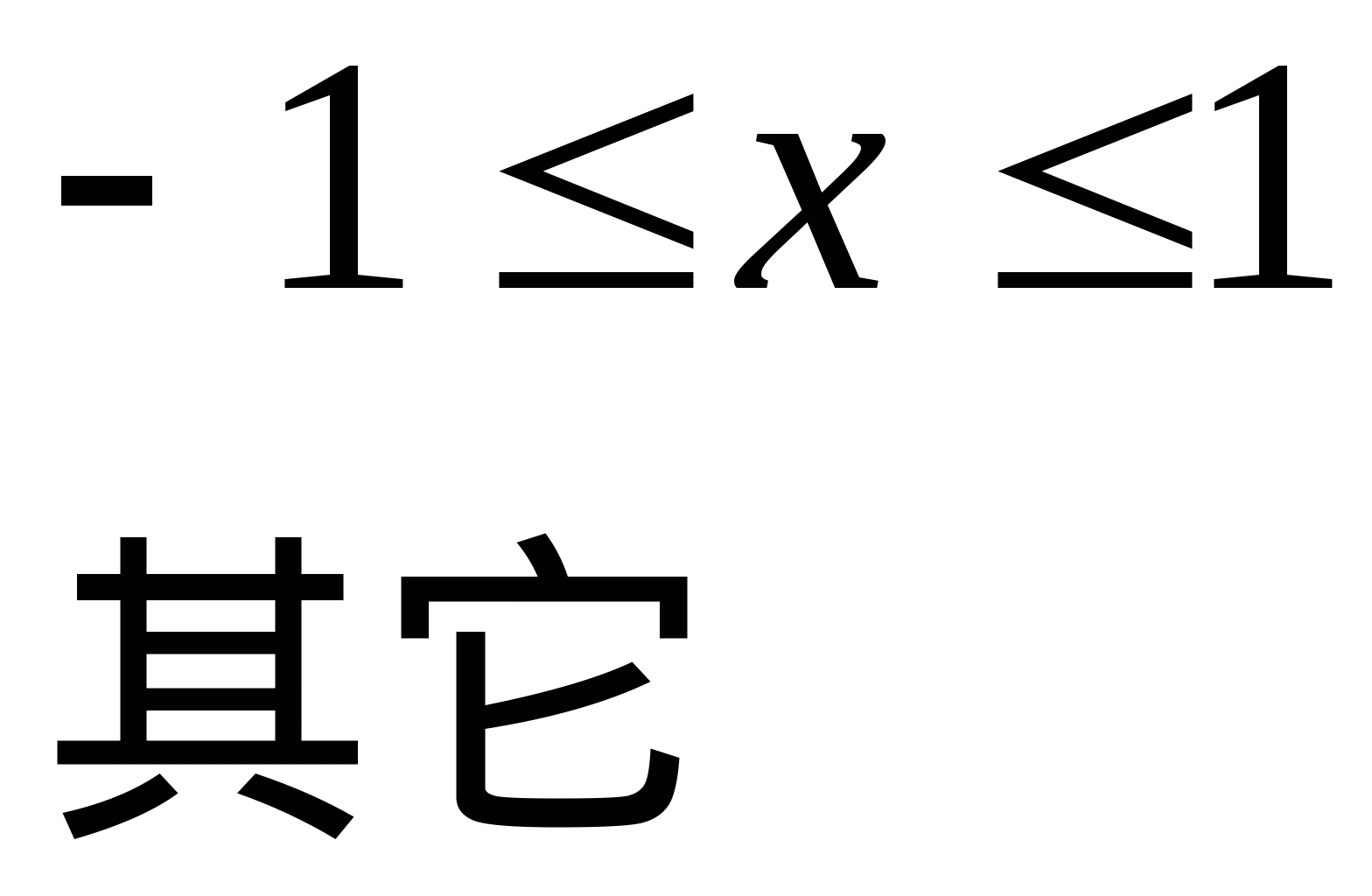 , ,
求(1)常数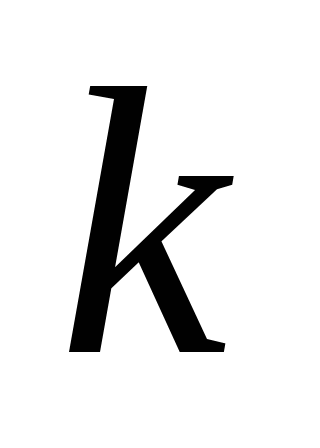 ;(2)分布函数 ;(2)分布函数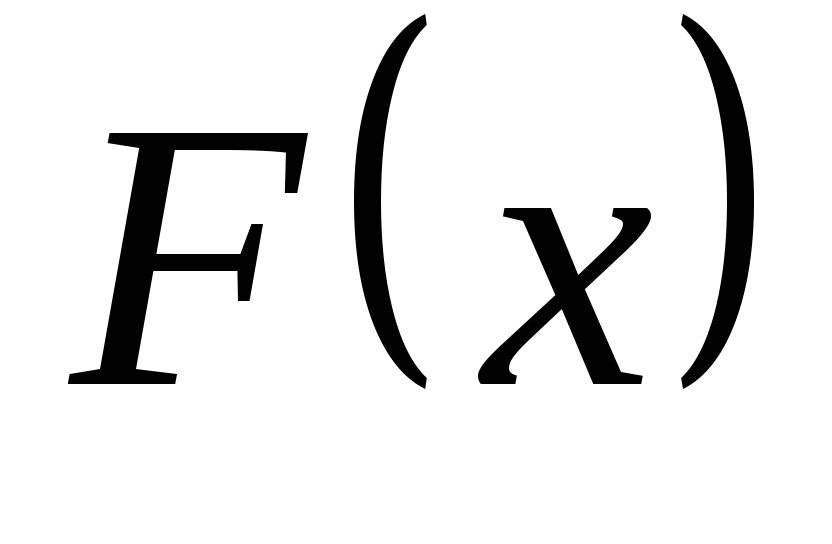 ;(3) ;(3)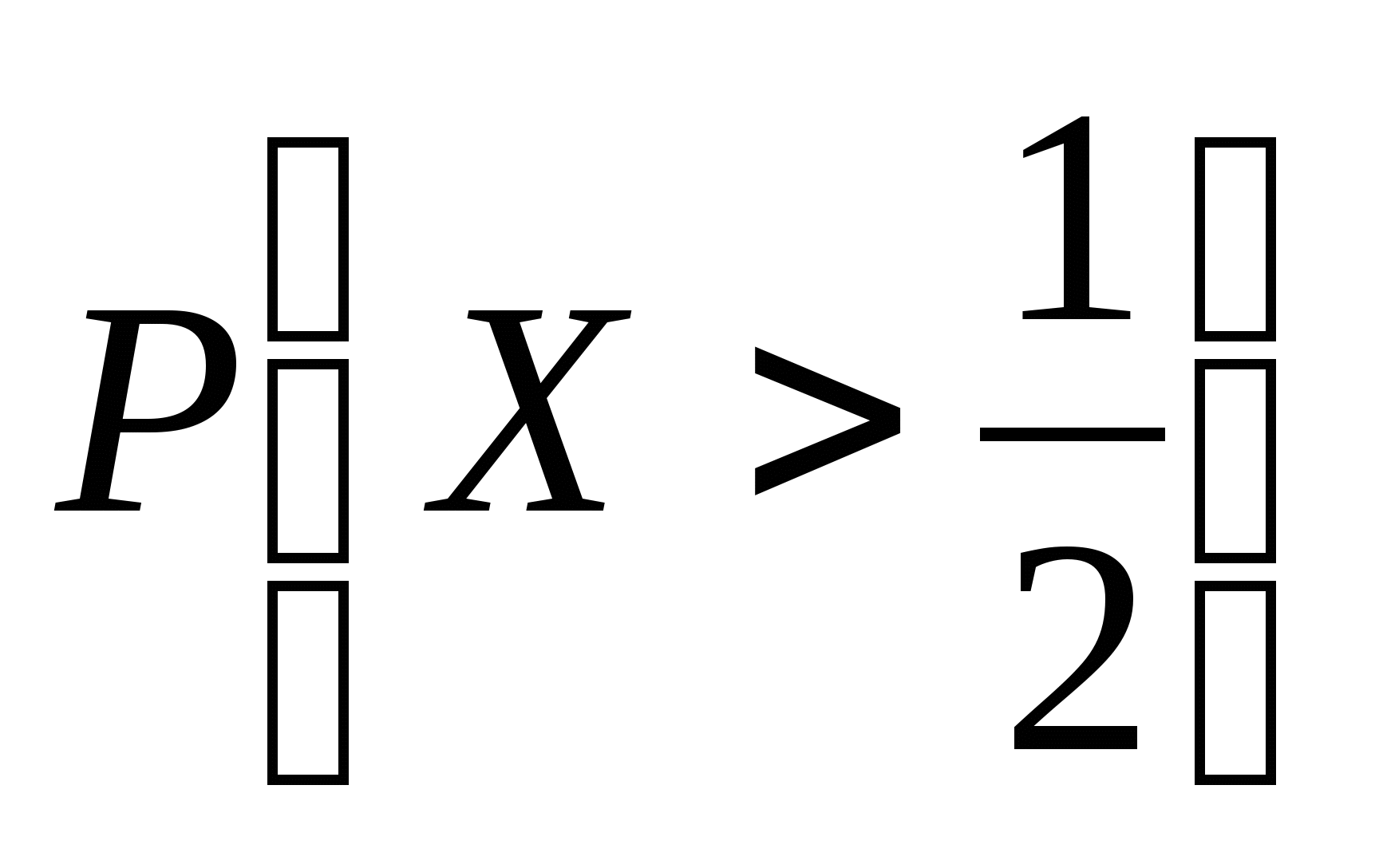 . . 二、几个常见的连续性随机变量的分布 1.均匀分布 设连续性随机变量 的密度函数为 的密度函数为 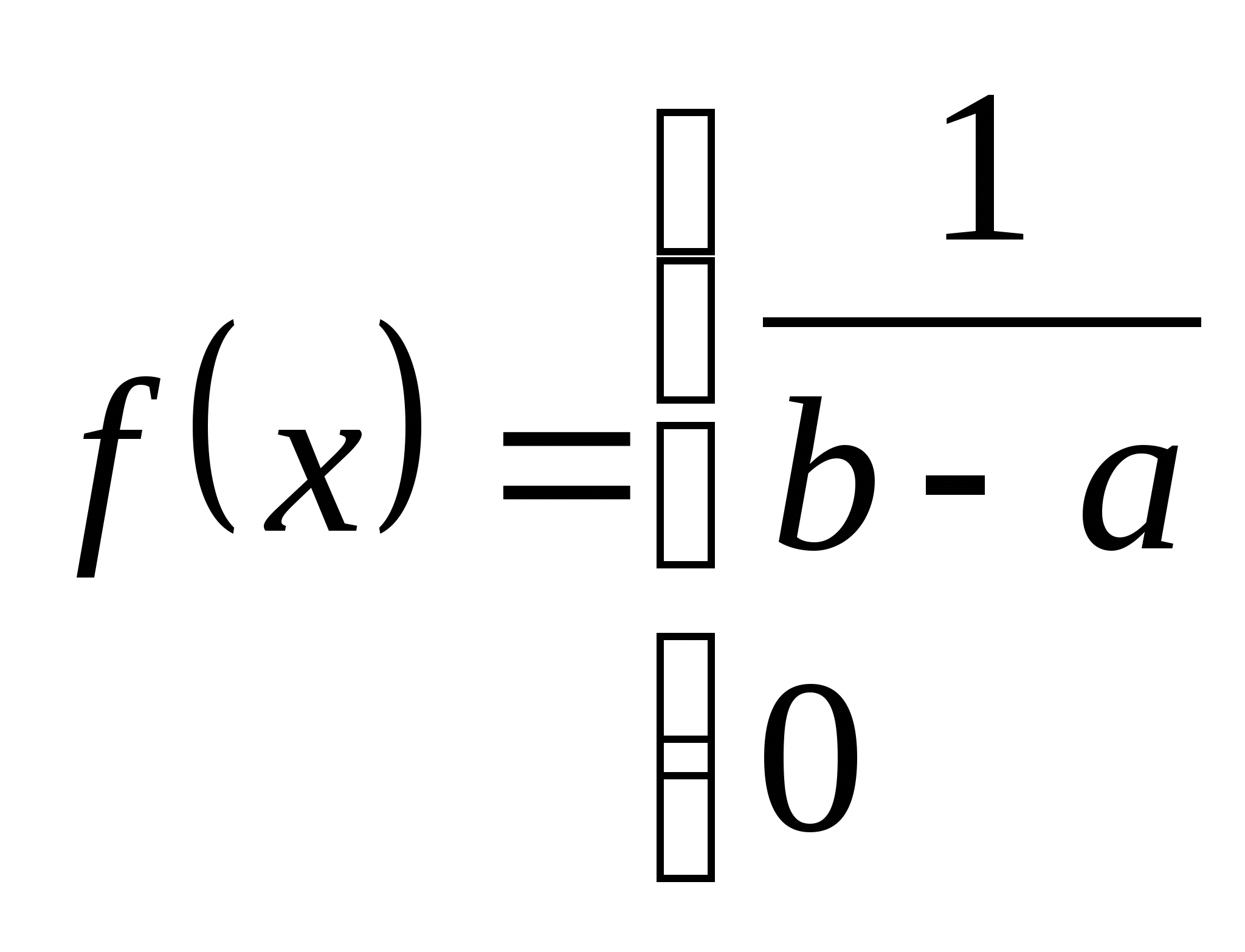 
则称 在区间 在区间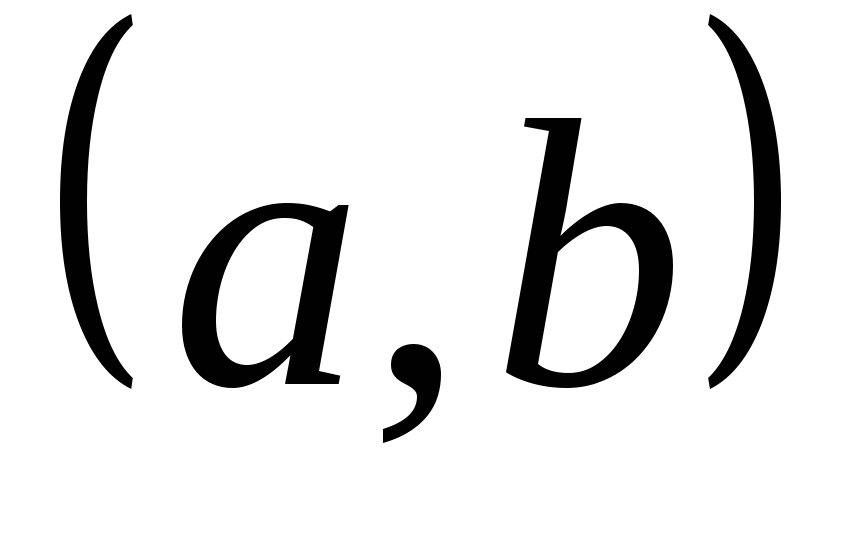 内服从均匀分布,记作 内服从均匀分布,记作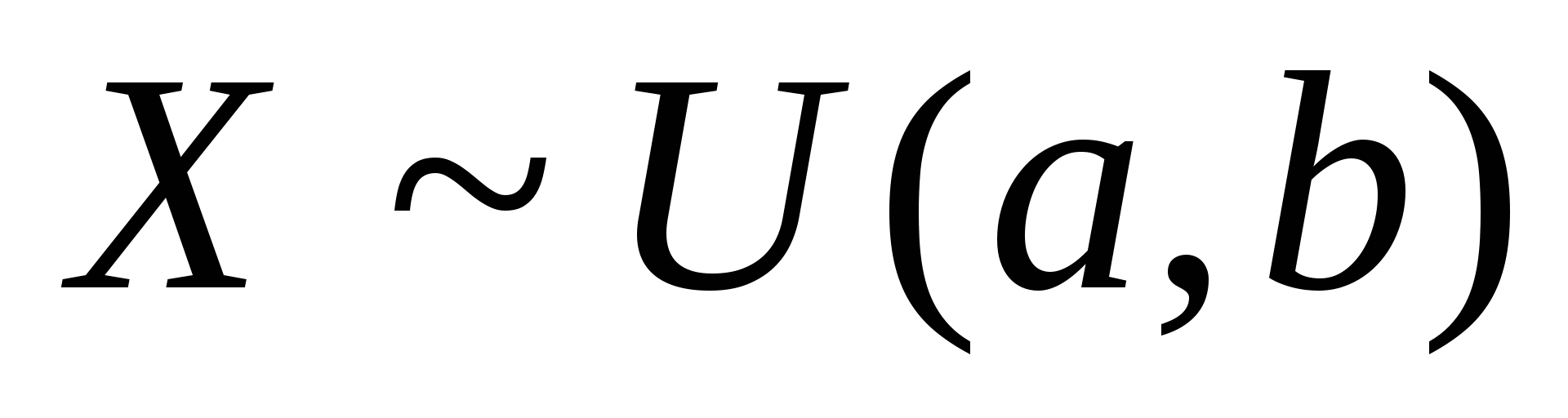 . . 均匀分布的特点是: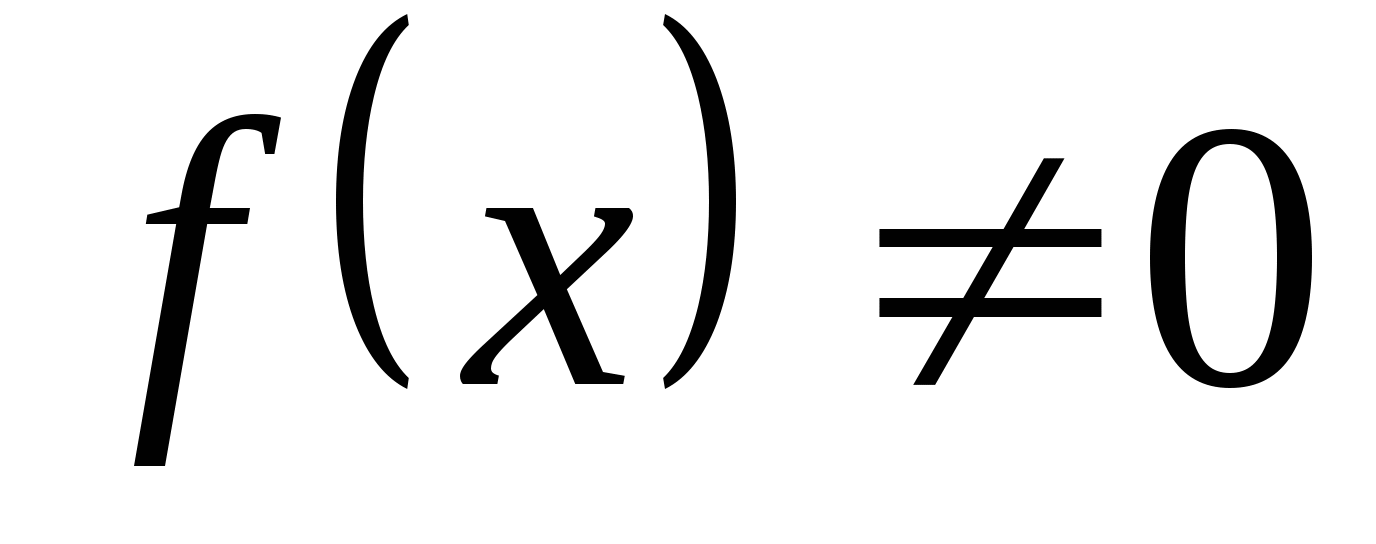 的值为该区间长度的倒数,在其它区间内,其值为零. 的值为该区间长度的倒数,在其它区间内,其值为零. 其分布函数为  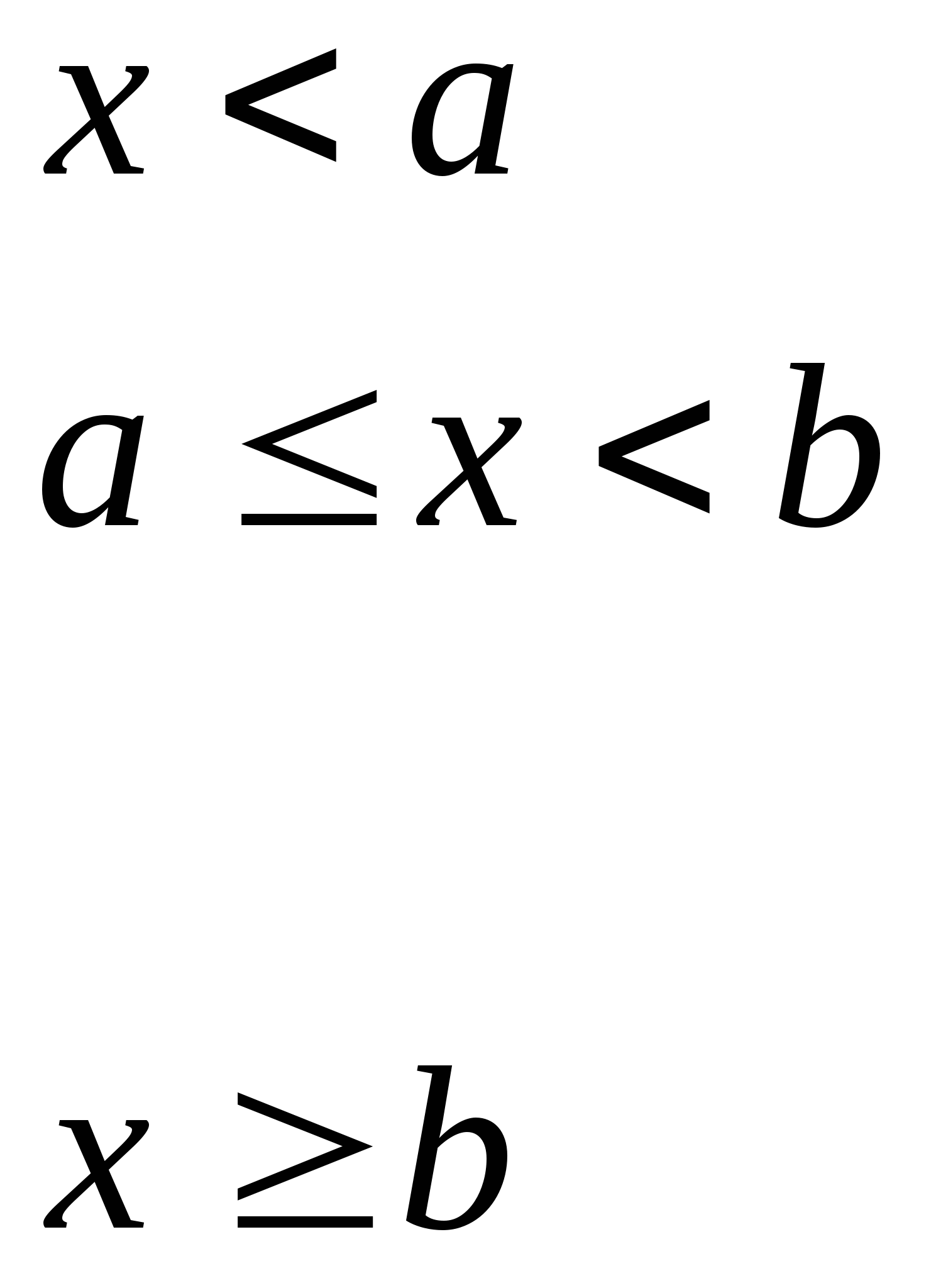
例4某公共汽车站早上6时起每隔15分钟开出一趟班车,假定某乘客在6时以后到达车站的时刻是随机的,则他等候乘车的时间长度 服从 服从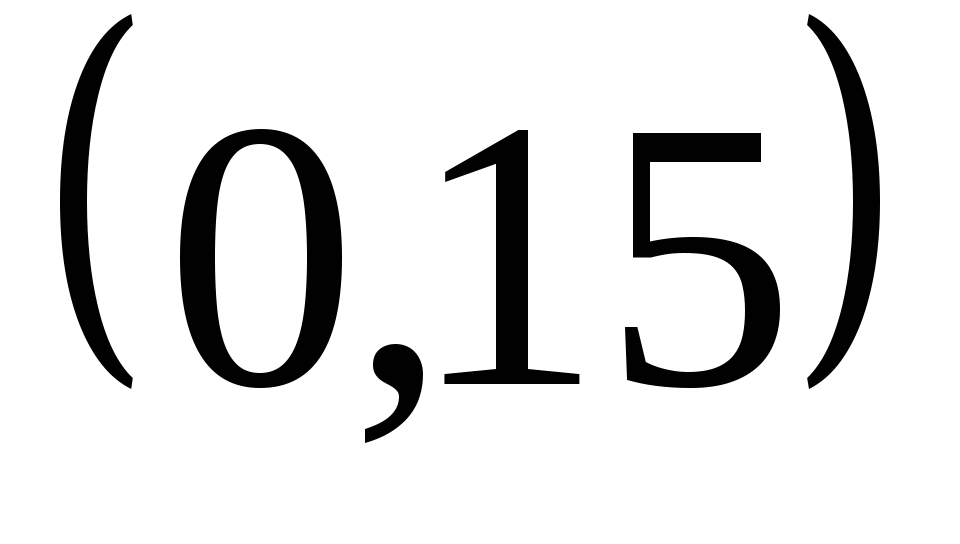 上的均匀分布,求该乘客等候乘车的时间少于5分钟的概率. 上的均匀分布,求该乘客等候乘车的时间少于5分钟的概率. 2.指数分布 设连续型随机变量 的密度函数为 的密度函数为 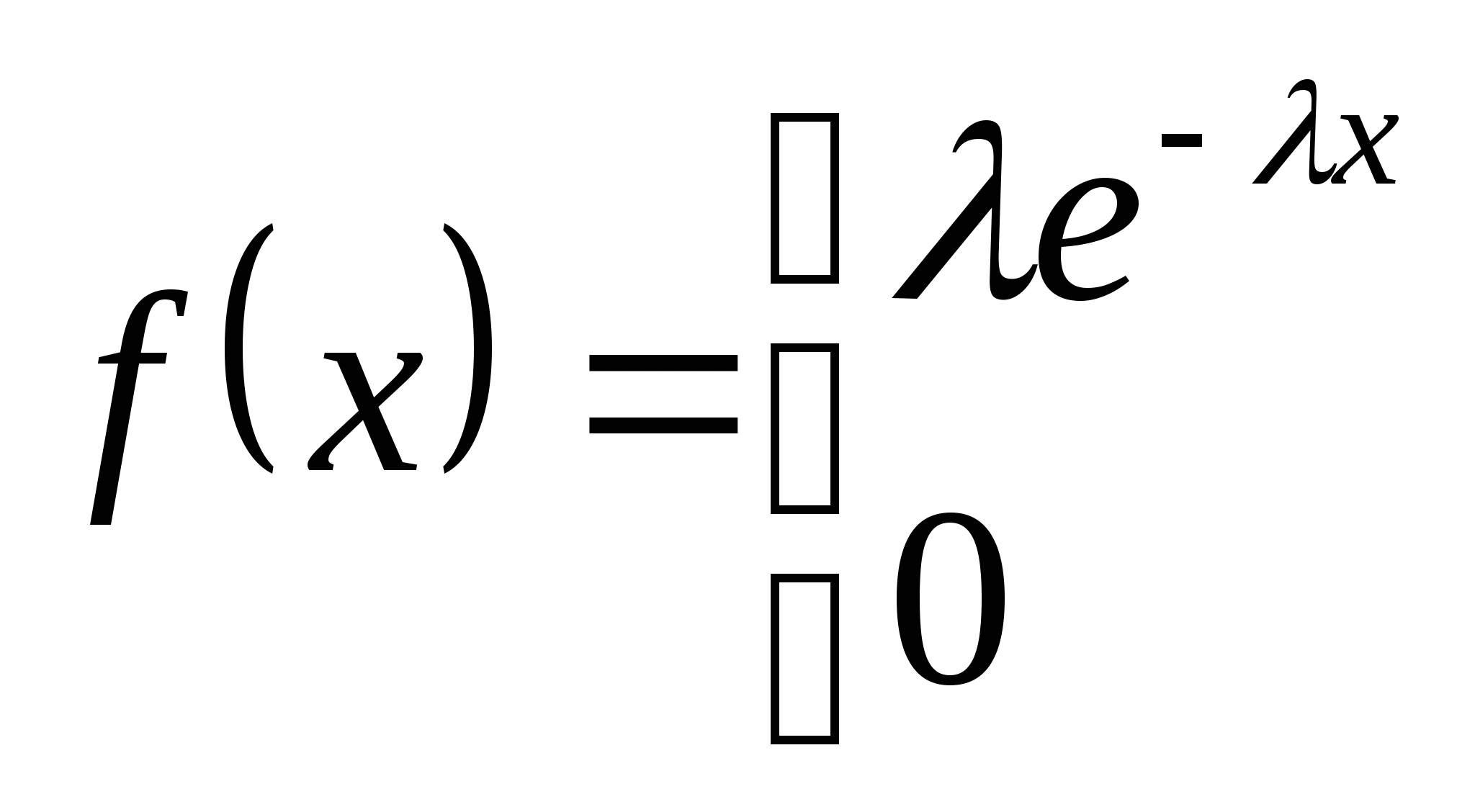 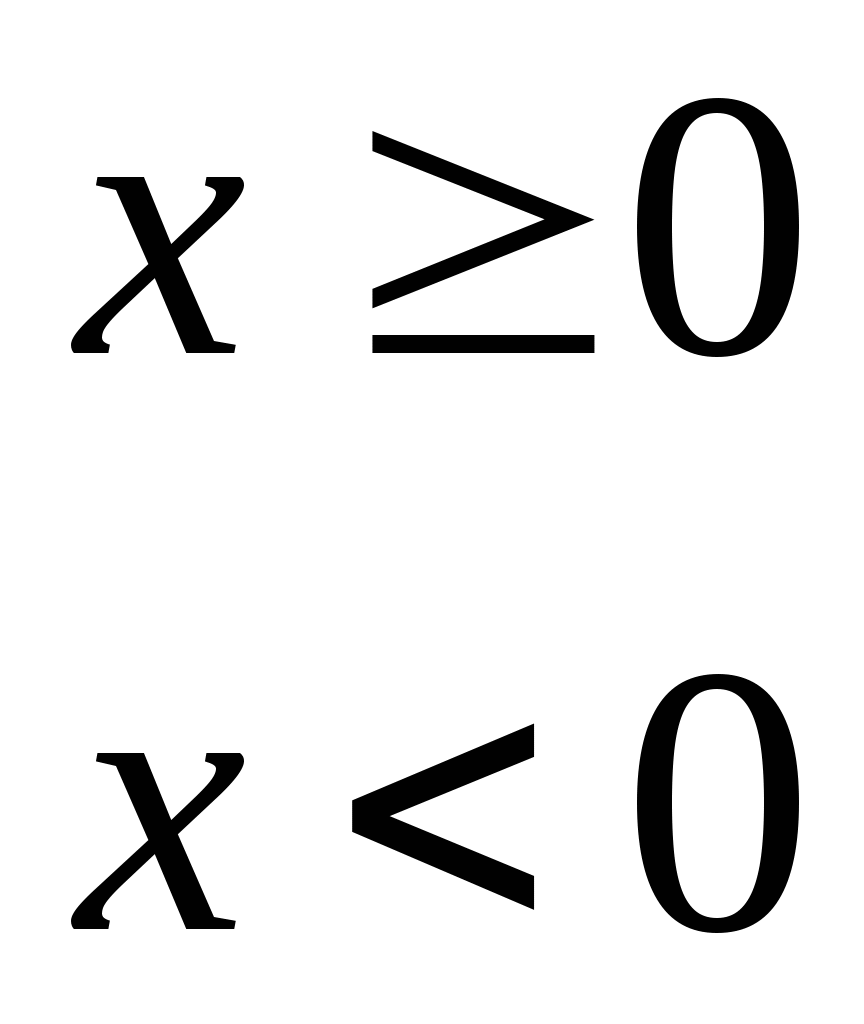
则称 服从于参数为 服从于参数为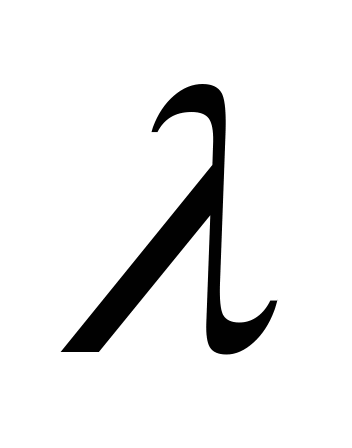 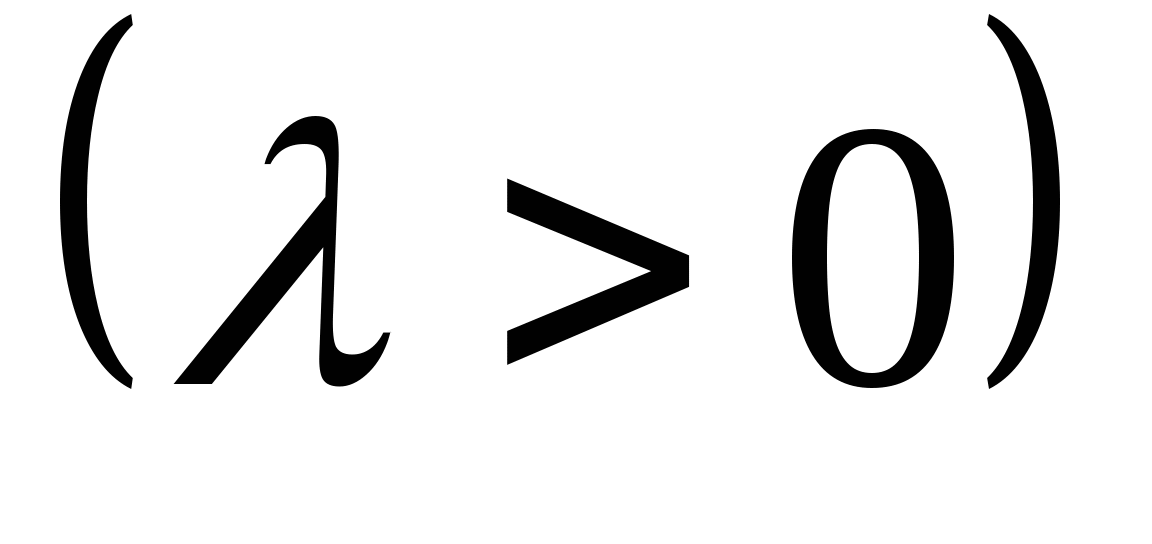 的指数分布,记作 的指数分布,记作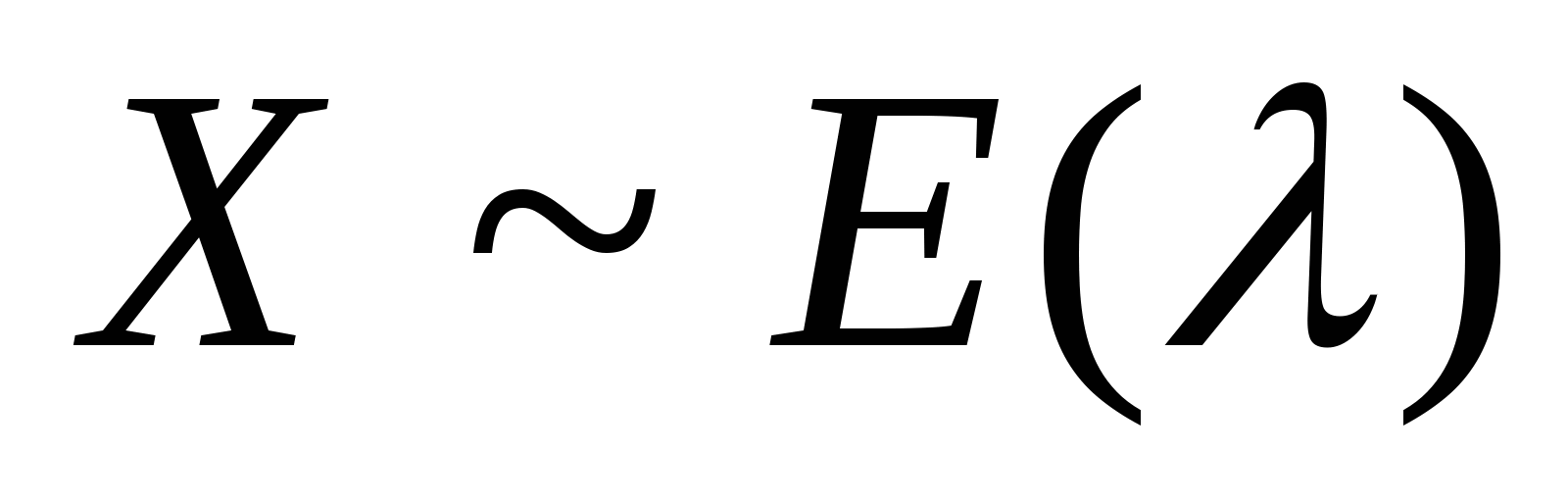 .其分布函数为 .其分布函数为  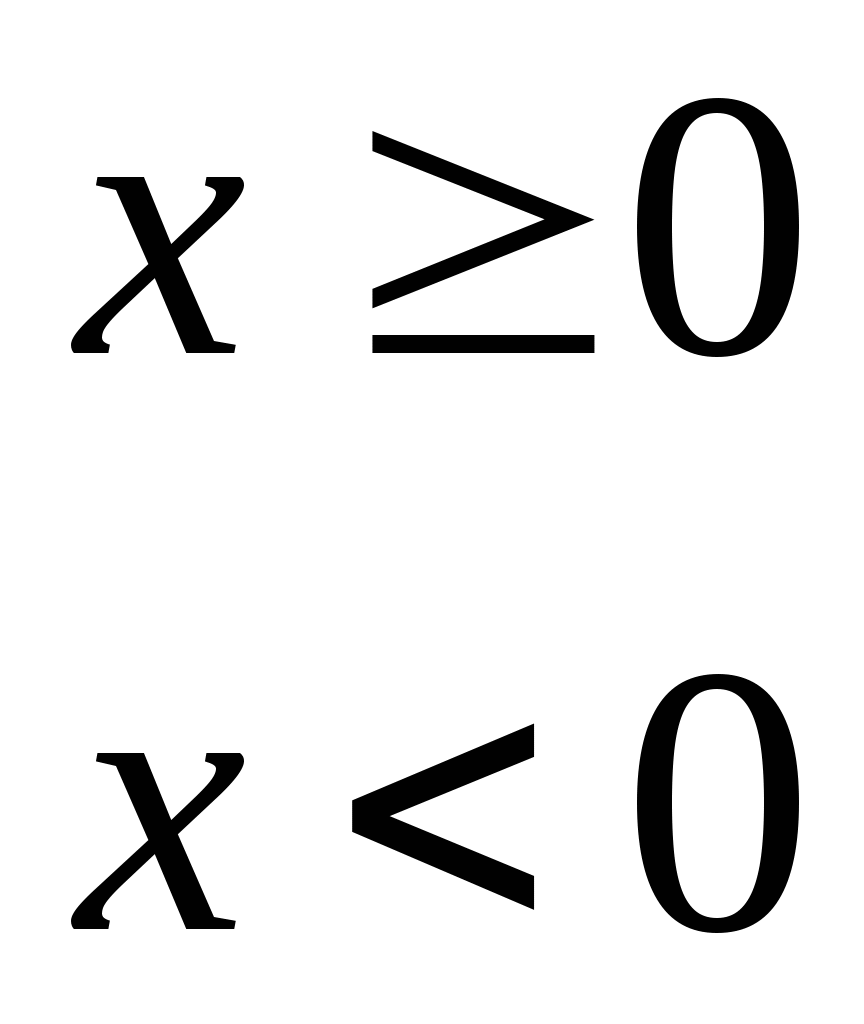
3. 正态分布 设连续型随机变量 的密度函数为: 的密度函数为:  , , 
其中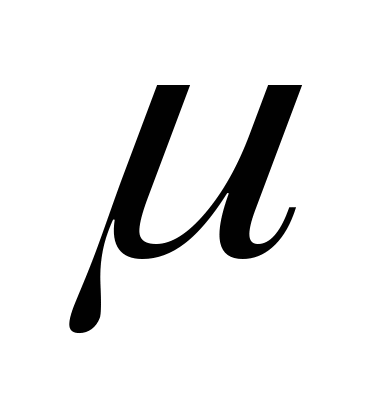 , ,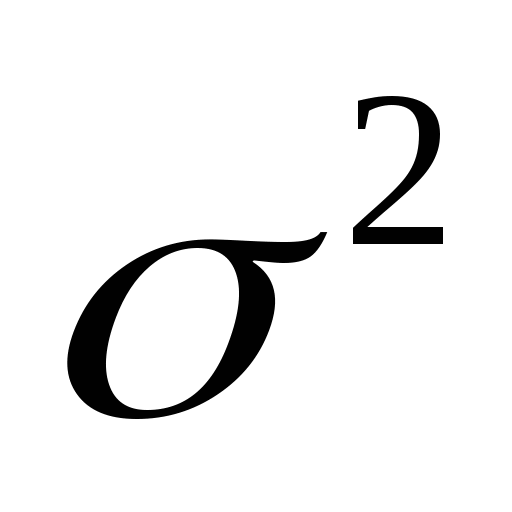 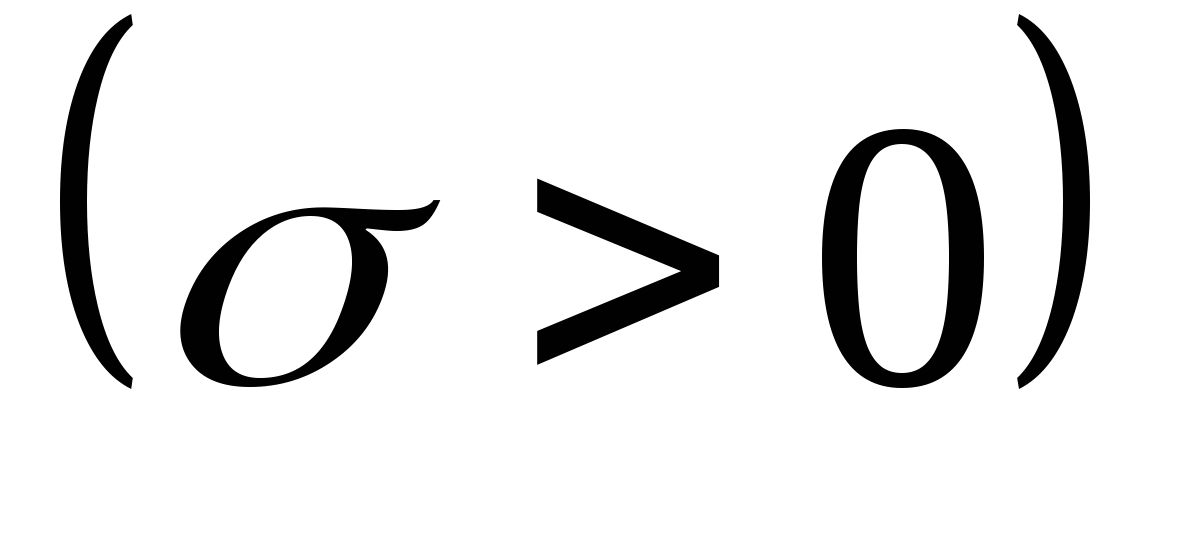 为常数,则称 为常数,则称 服从于参数为 服从于参数为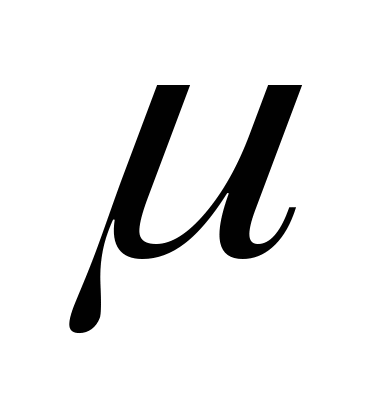 , ,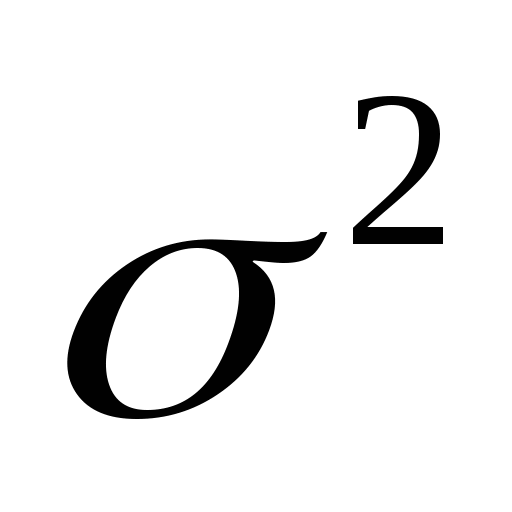 的正态分布,记作 的正态分布,记作 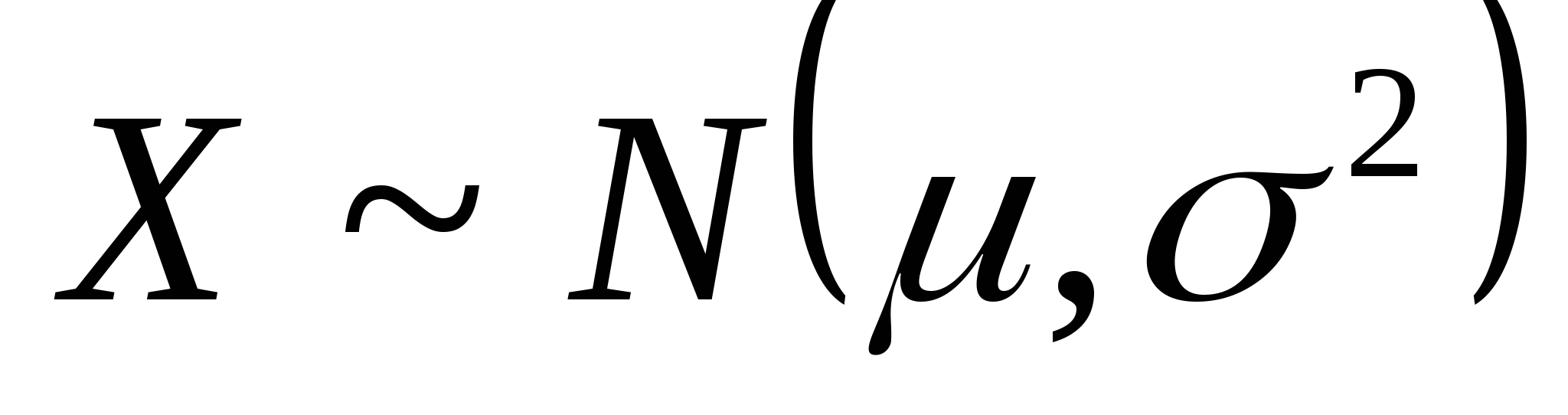 . .
当参数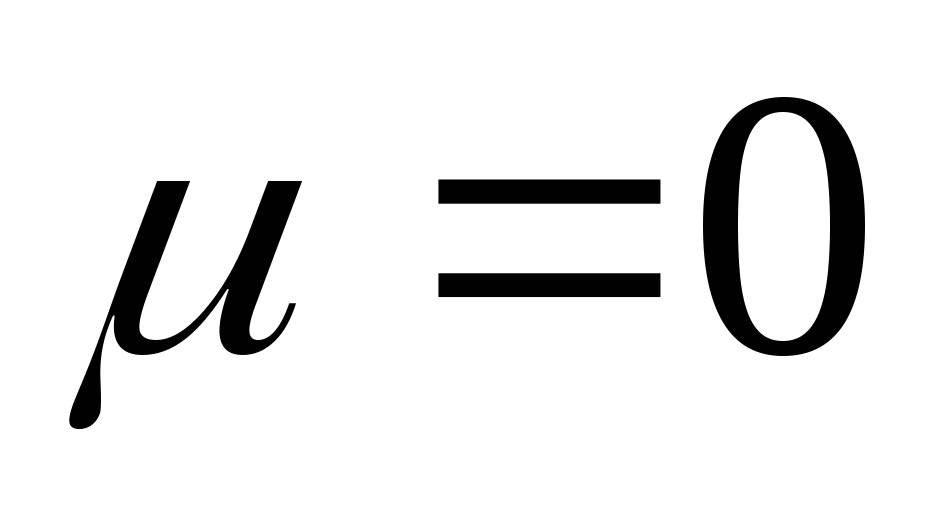 , ,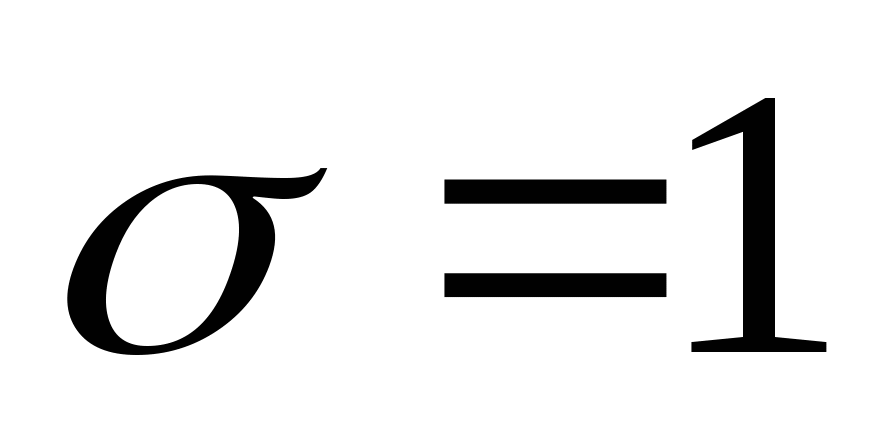 时,即 时,即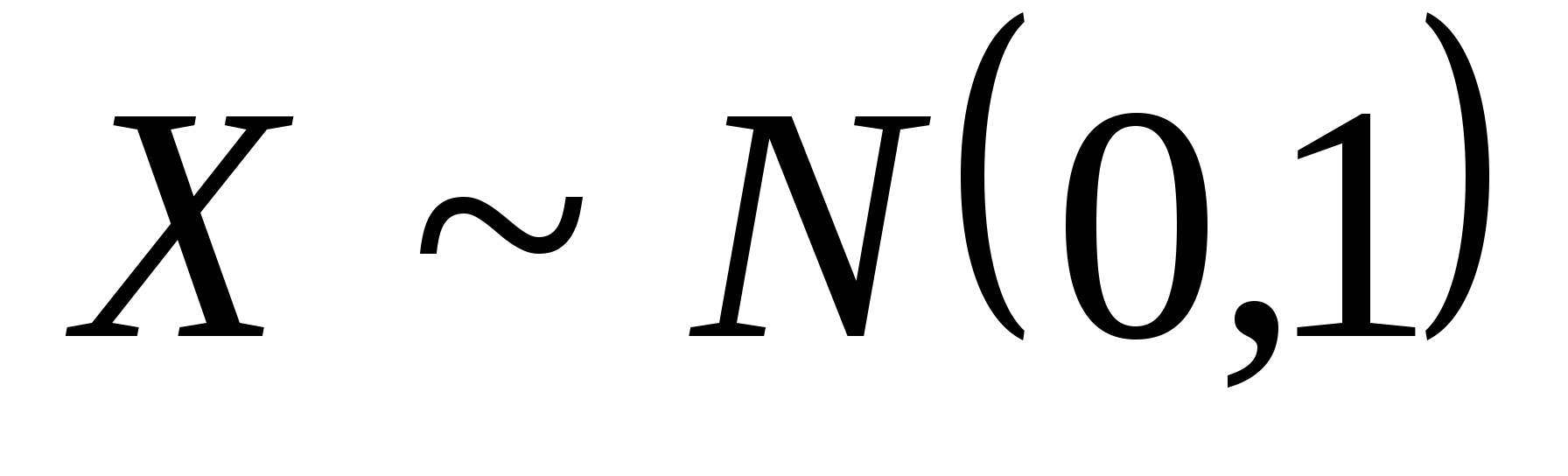 ,称 ,称 服从标准正态分布.用 服从标准正态分布.用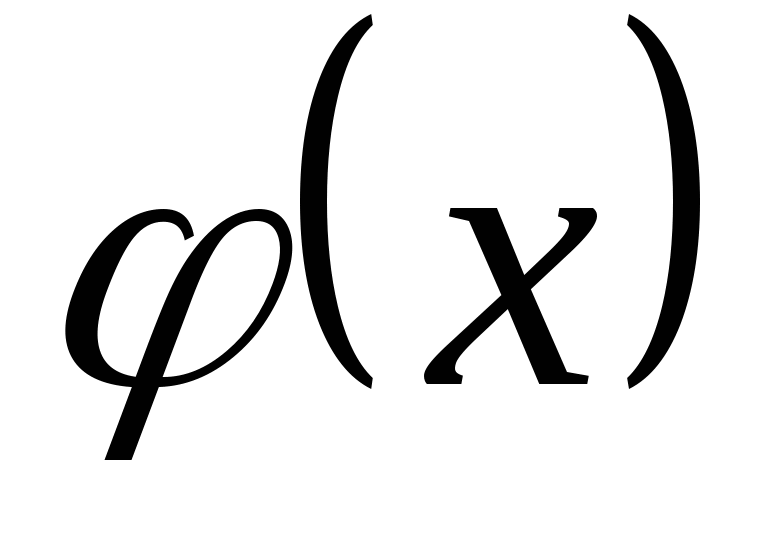 与 与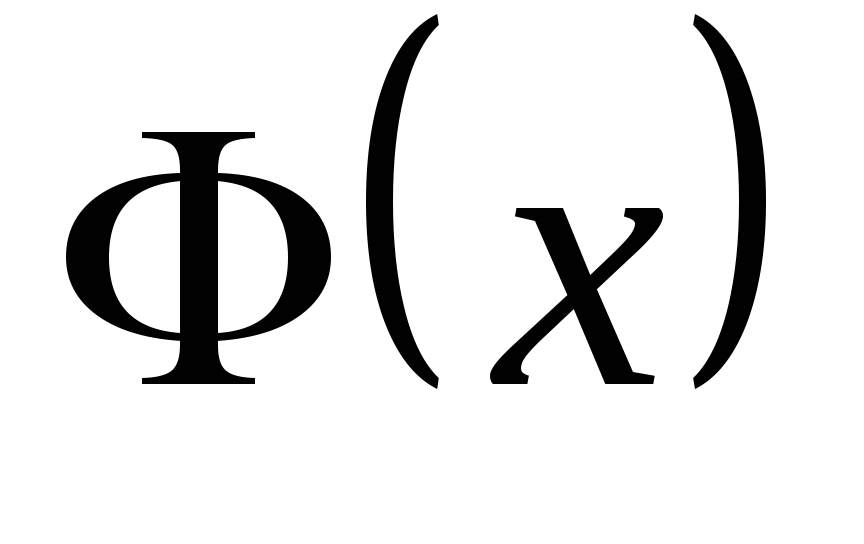 分别表示 分别表示 的密度函数和分布函数,即 的密度函数和分布函数,即 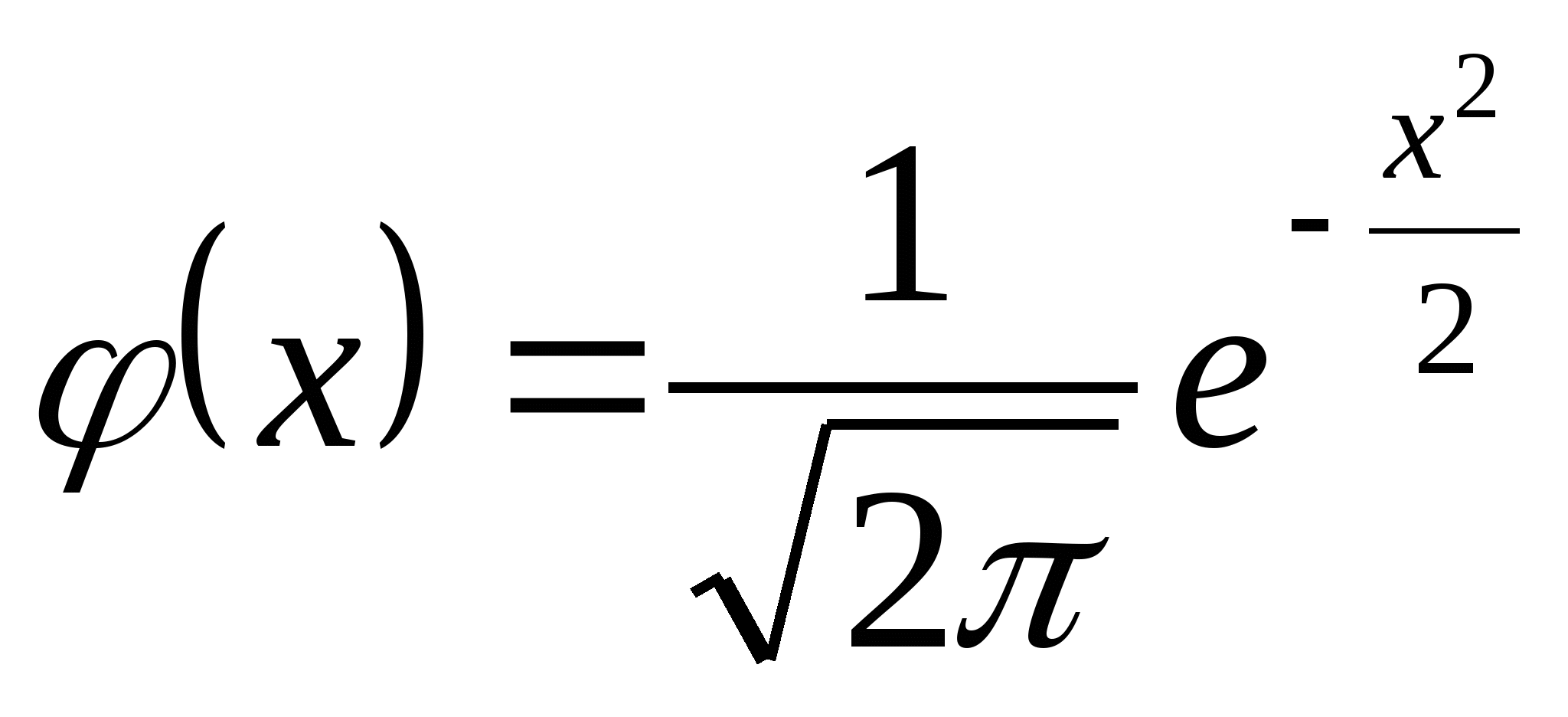 , ,
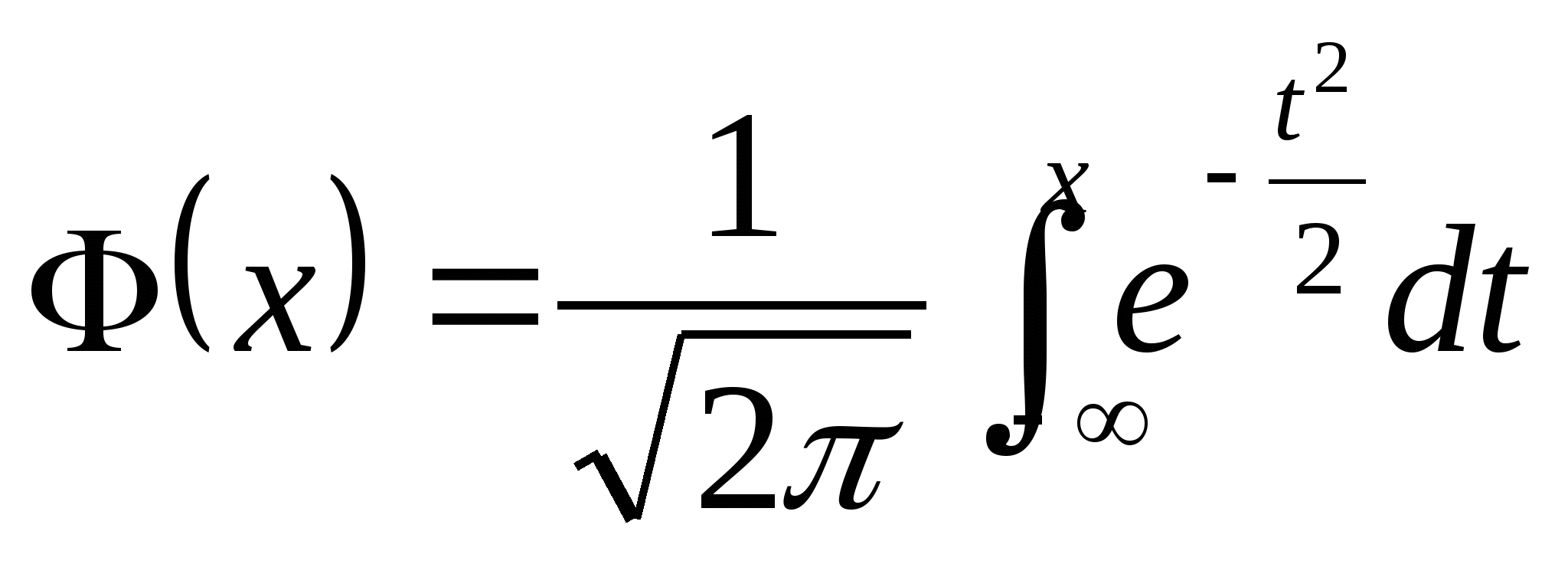 , , . .
函数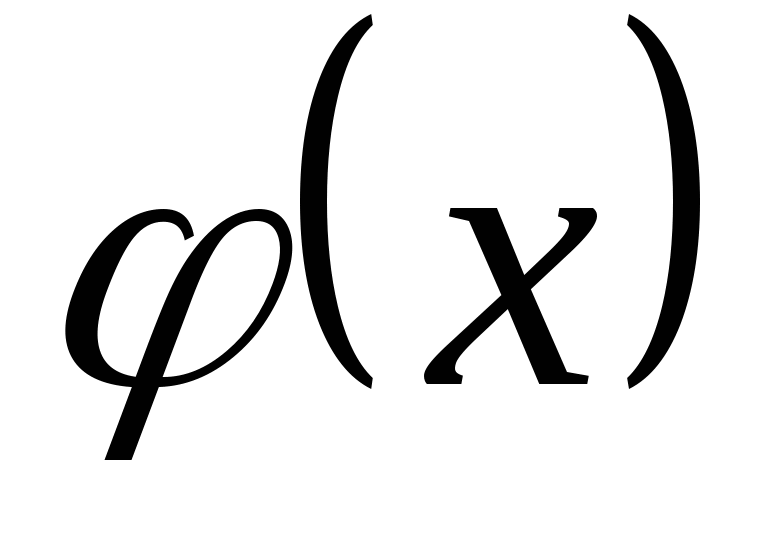 与 与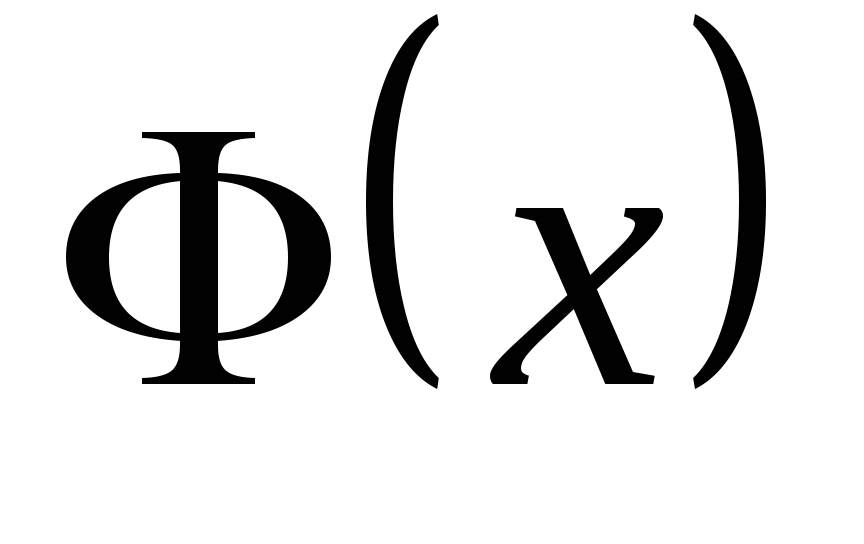 具有下面的性质: 具有下面的性质: (1)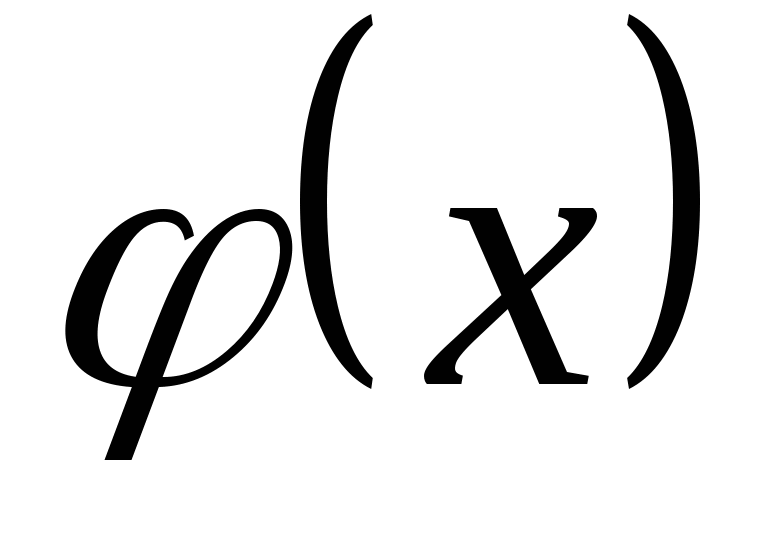 是偶函数;(2)当 是偶函数;(2)当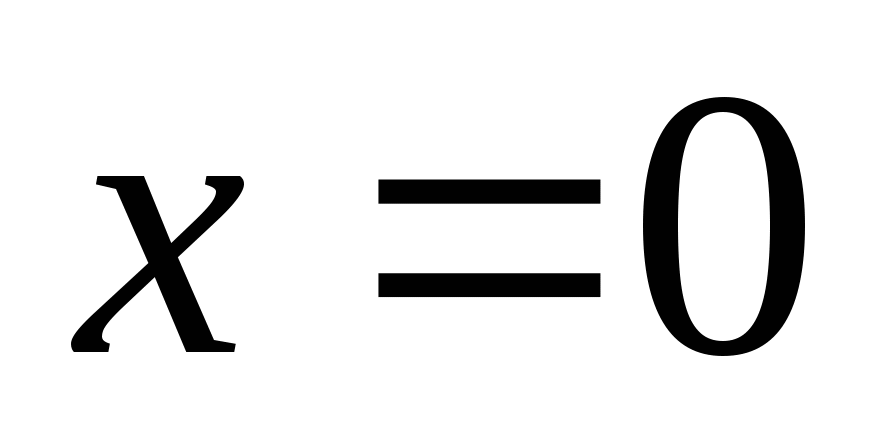 时, 时,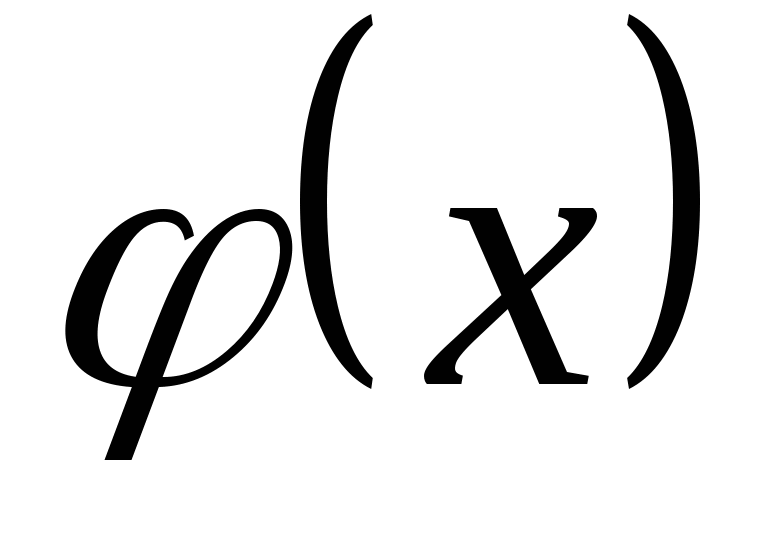 取最大值 取最大值 ; ; (3)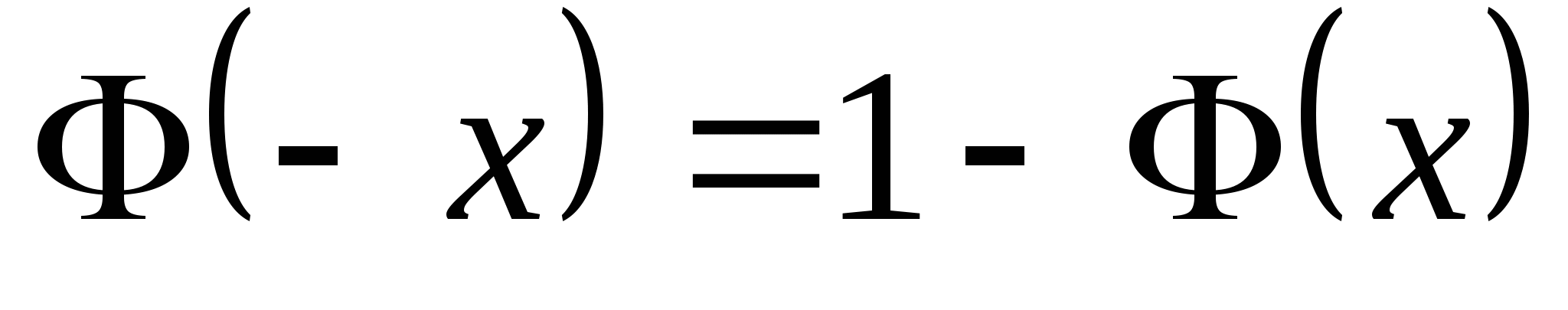 ;(4) ;(4)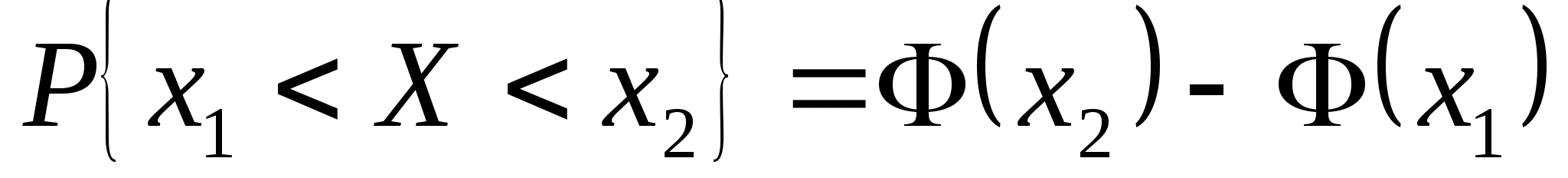 . . 计算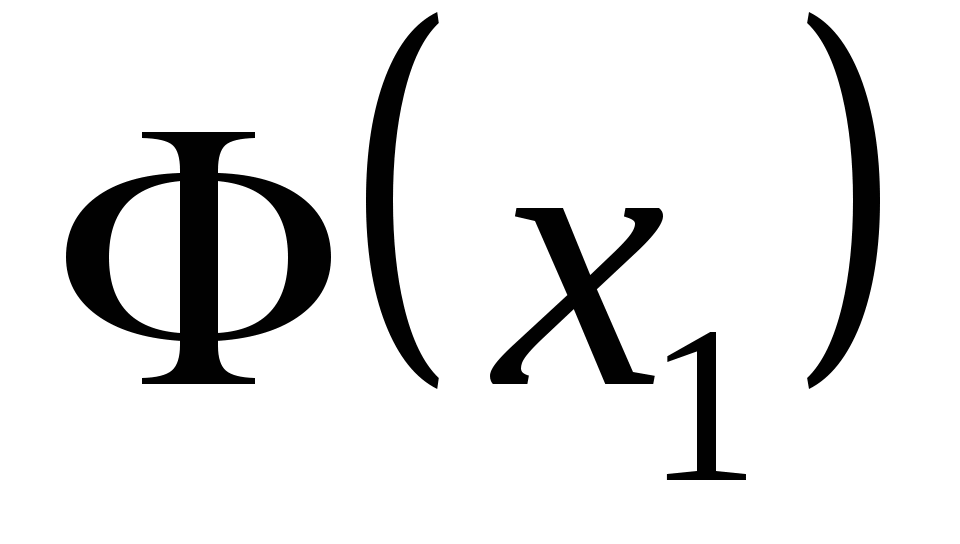 、 、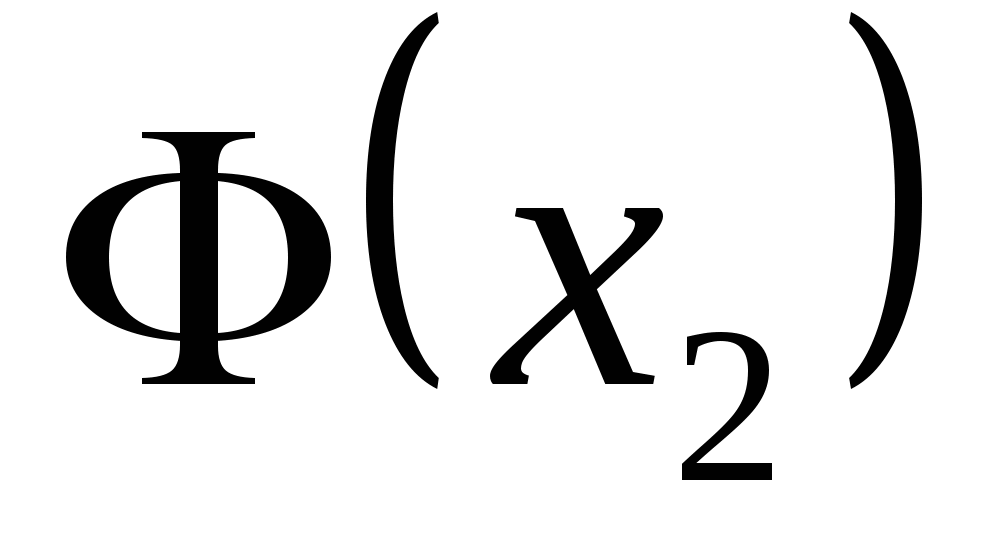 可查附表 可查附表 (标准正态分布表). (标准正态分布表). 例 已知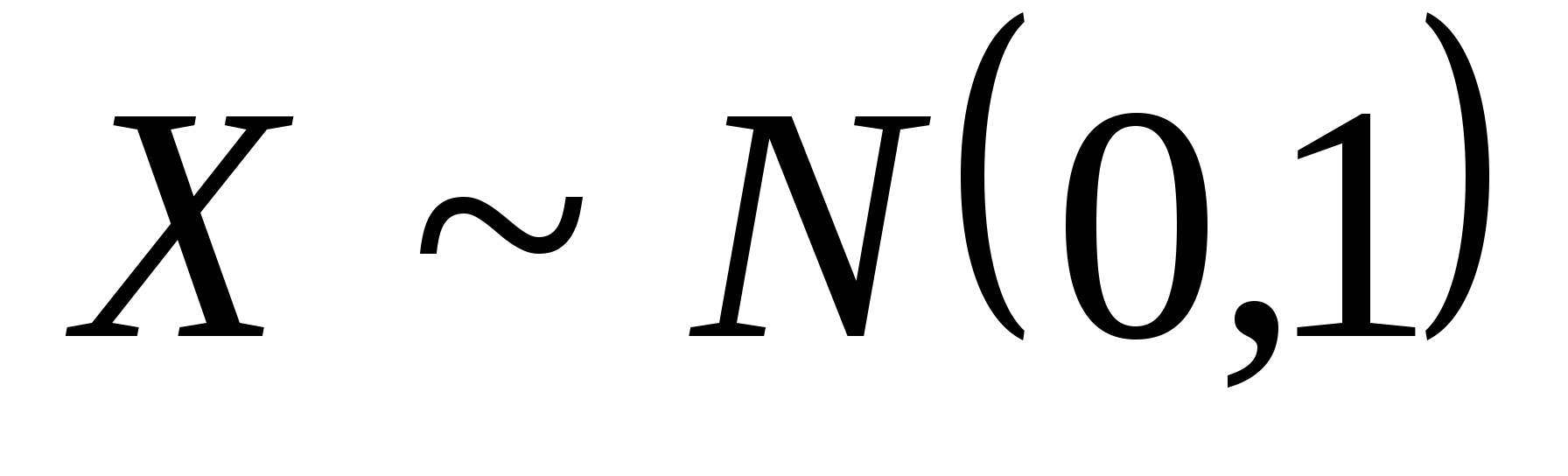 求(1) 求(1)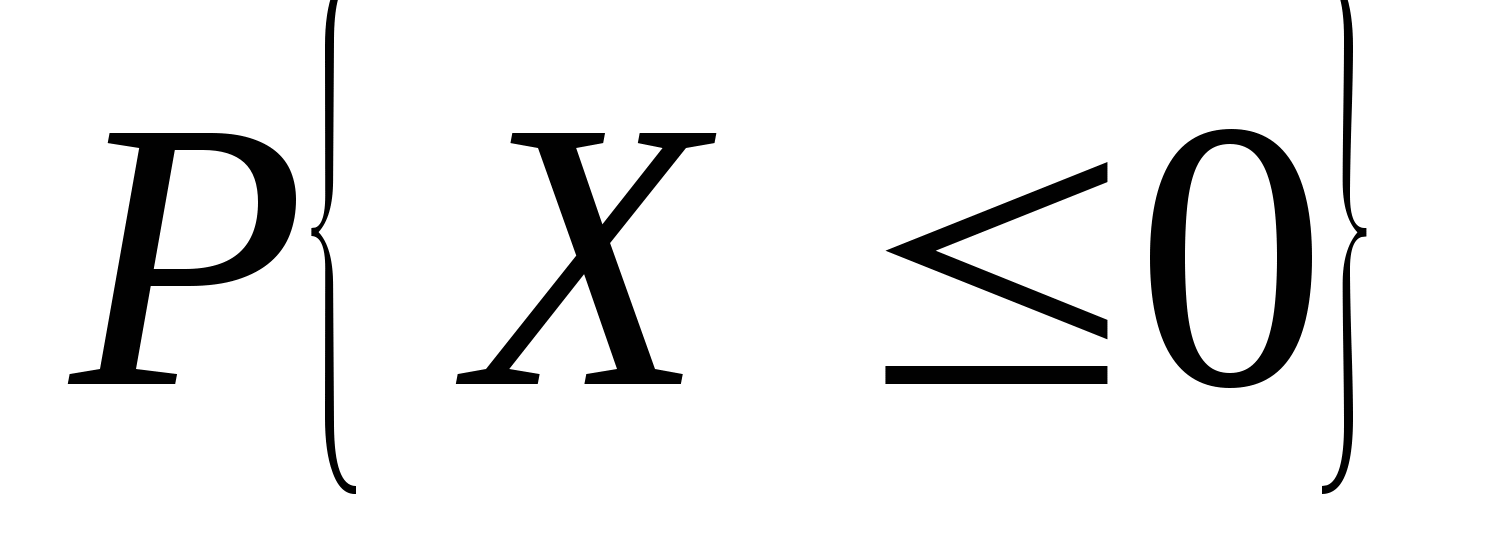 ; (2) ; (2)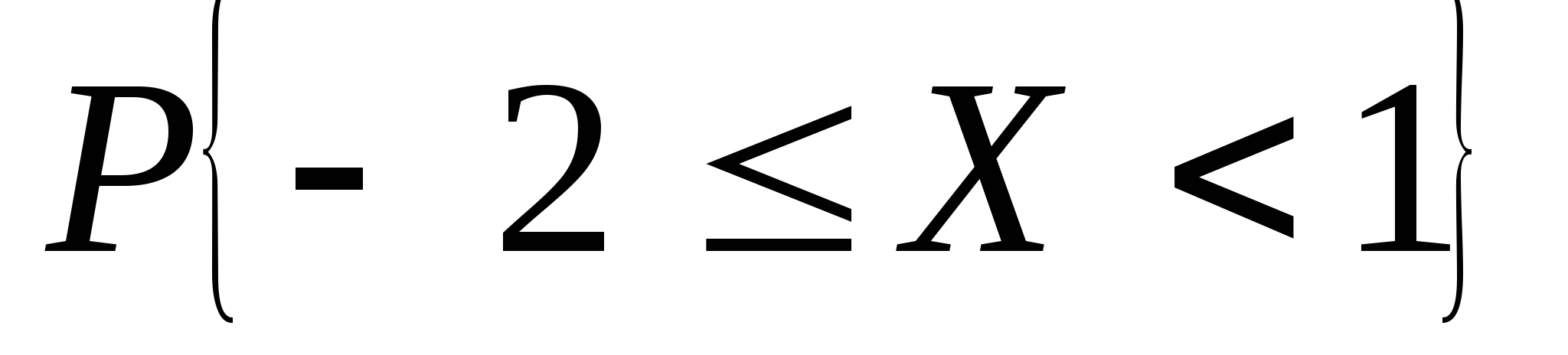 ; (3) ; (3)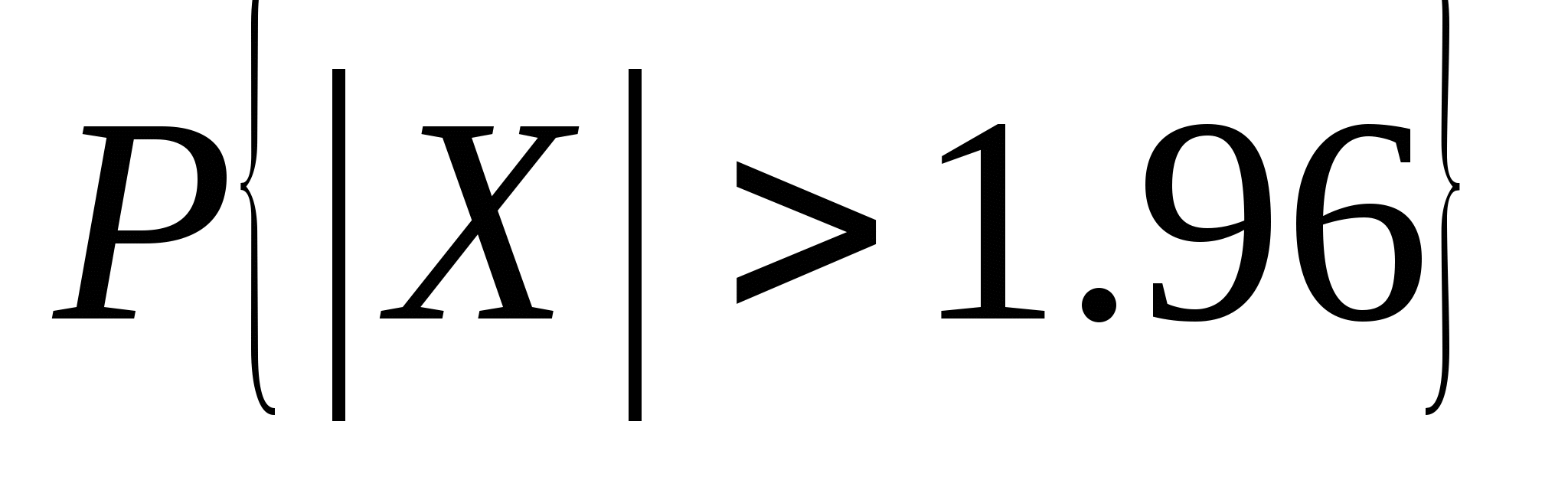 若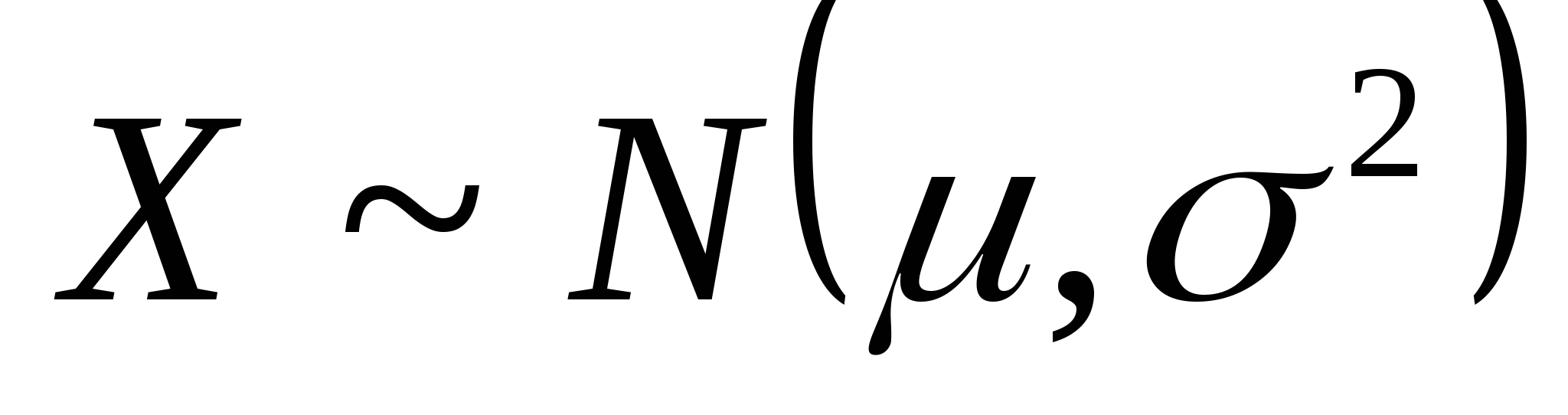 ,则通过变换 ,则通过变换 ,将 ,将 的分布函数化成标准型,即 的分布函数化成标准型,即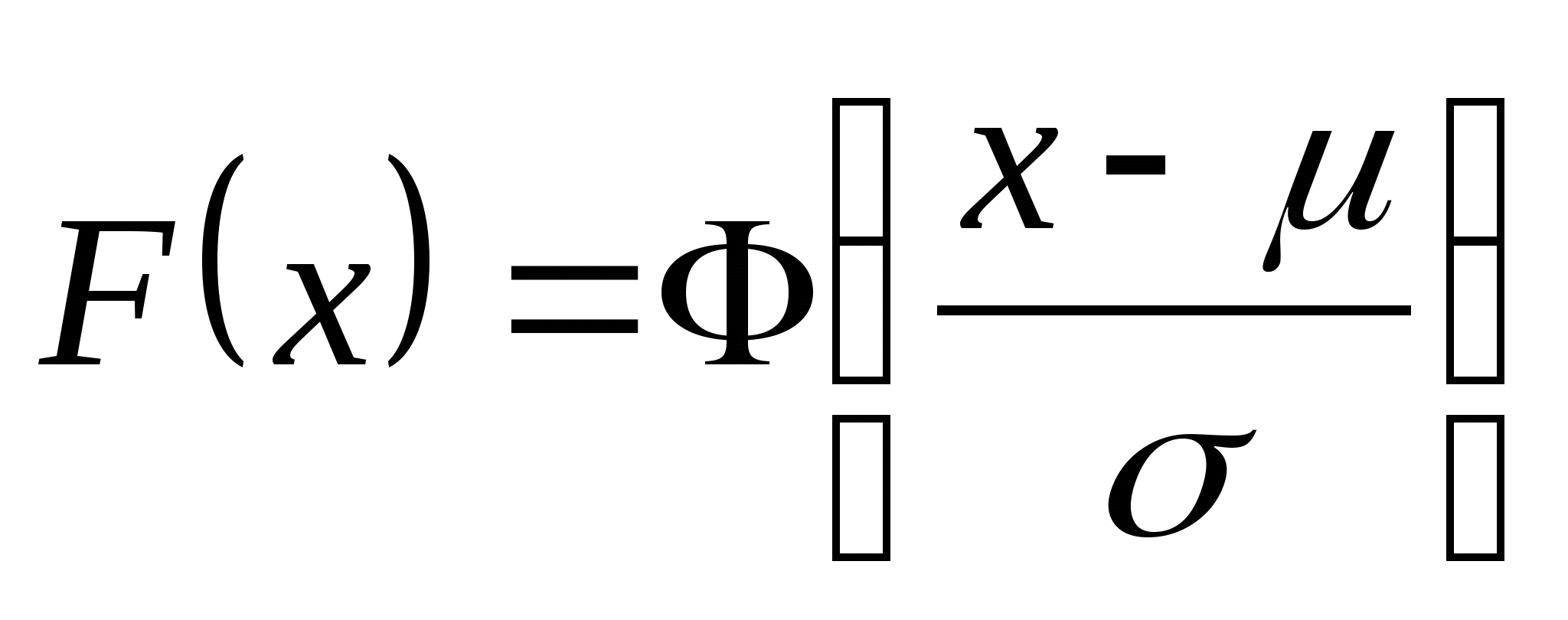 例 设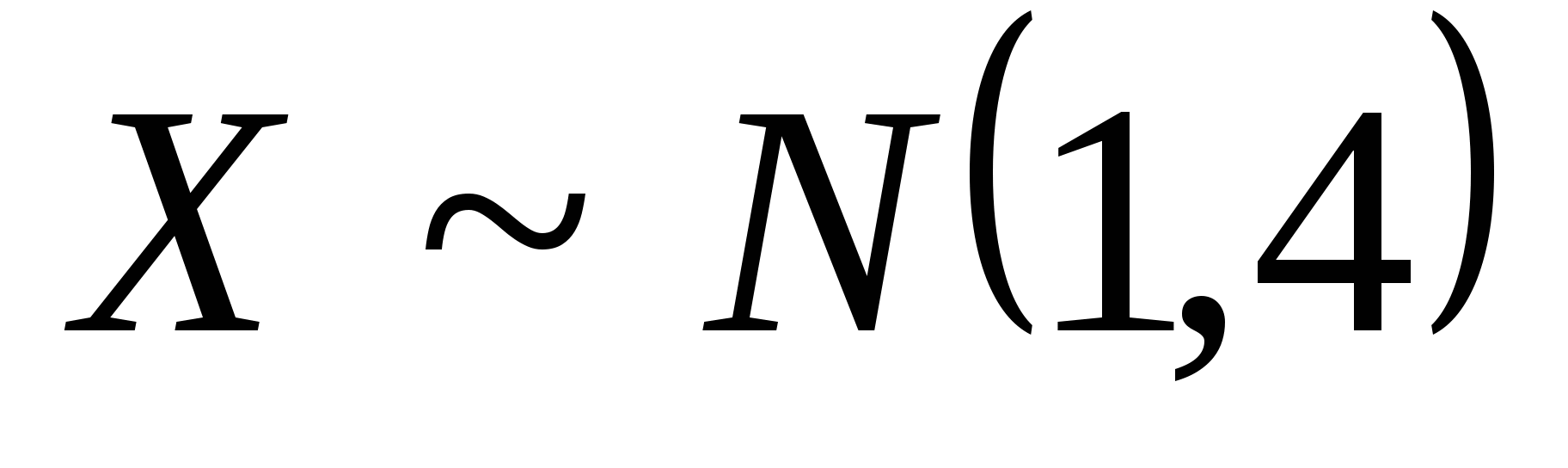 ,求(1) ,求(1)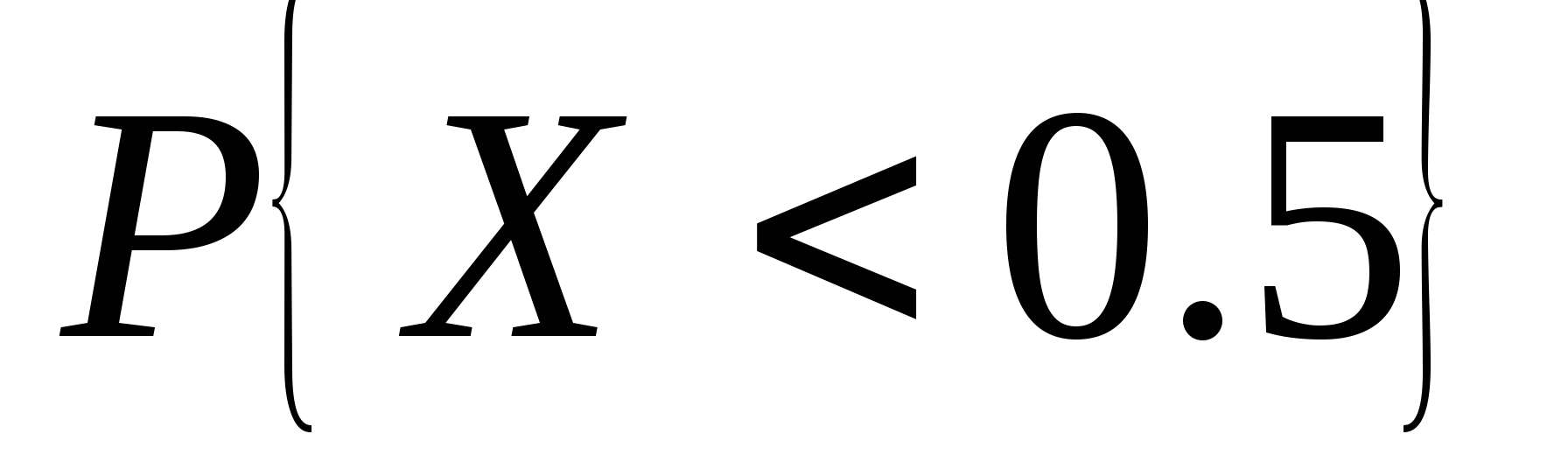 ;(2) ;(2)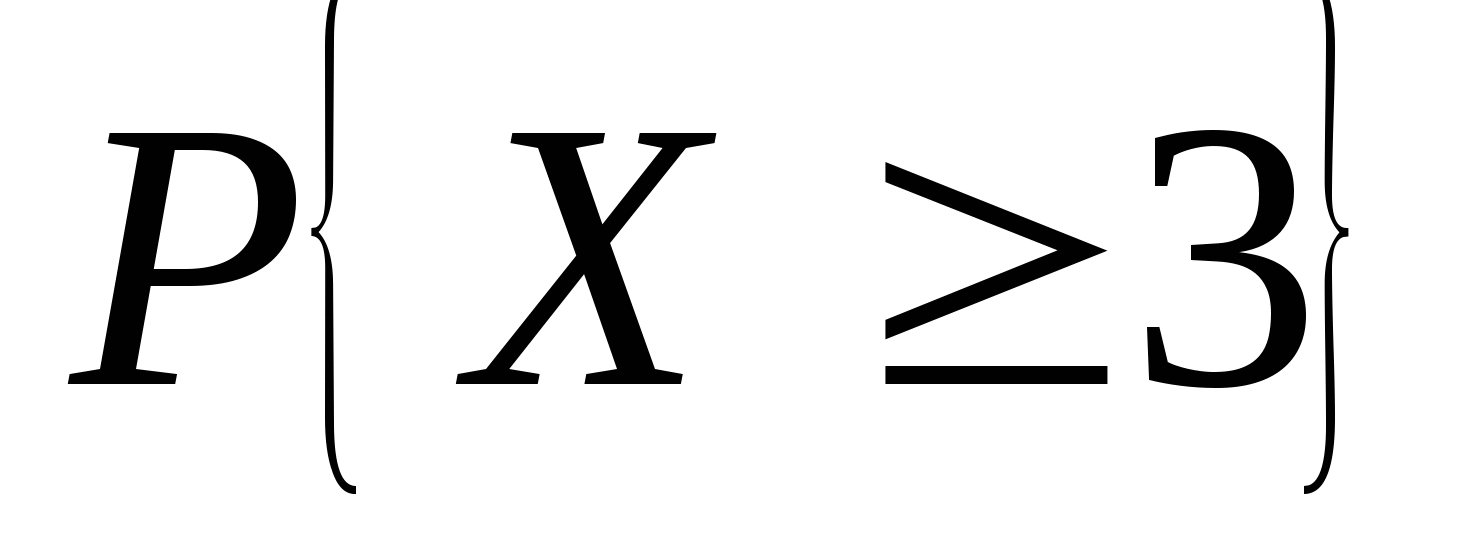 ;(3) ;(3)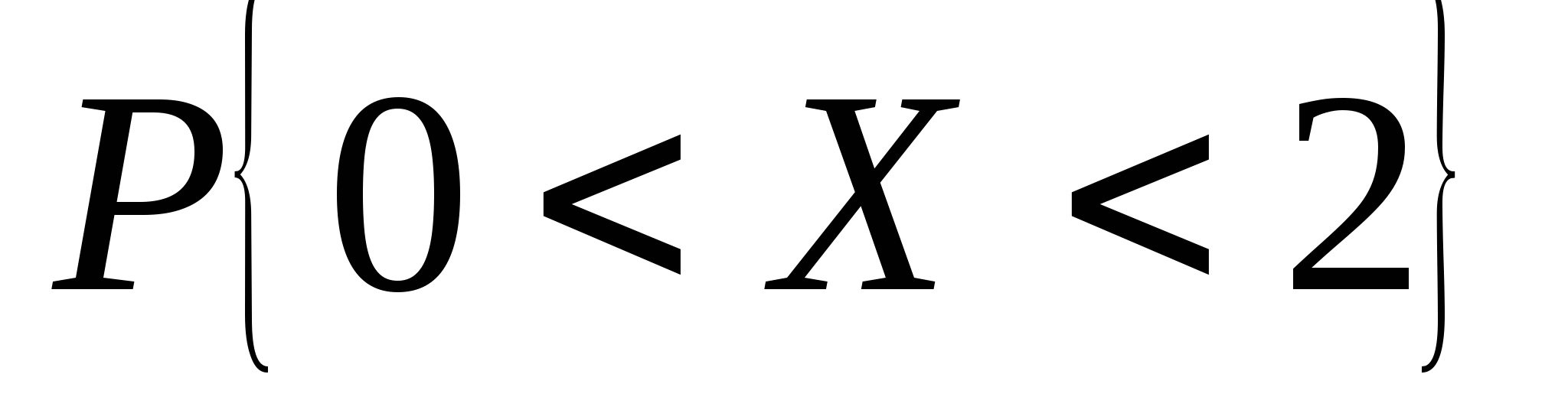 . . 第三节 随机变量函数的分布 设 是随机变量, 是随机变量,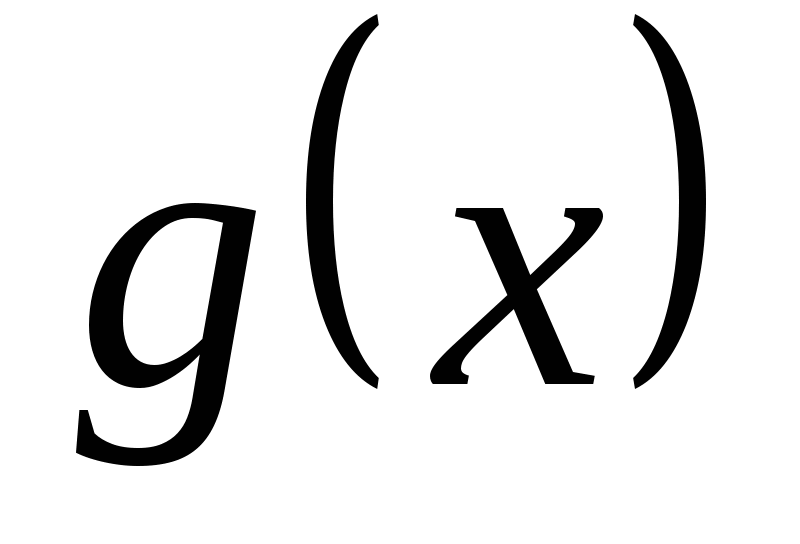 是一实函数,则 是一实函数,则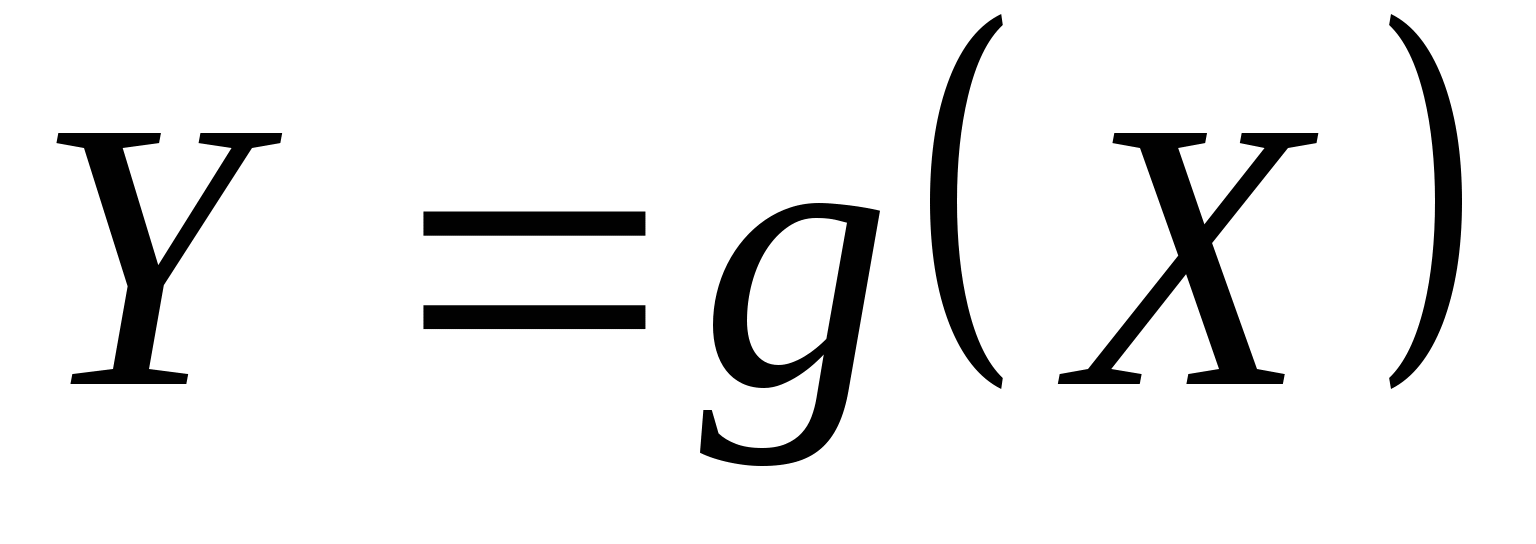 也是随机变量,则称Y是随机变量 也是随机变量,则称Y是随机变量 的函数.本节将讨论已知 的函数.本节将讨论已知 的分布,求它的函数 的分布,求它的函数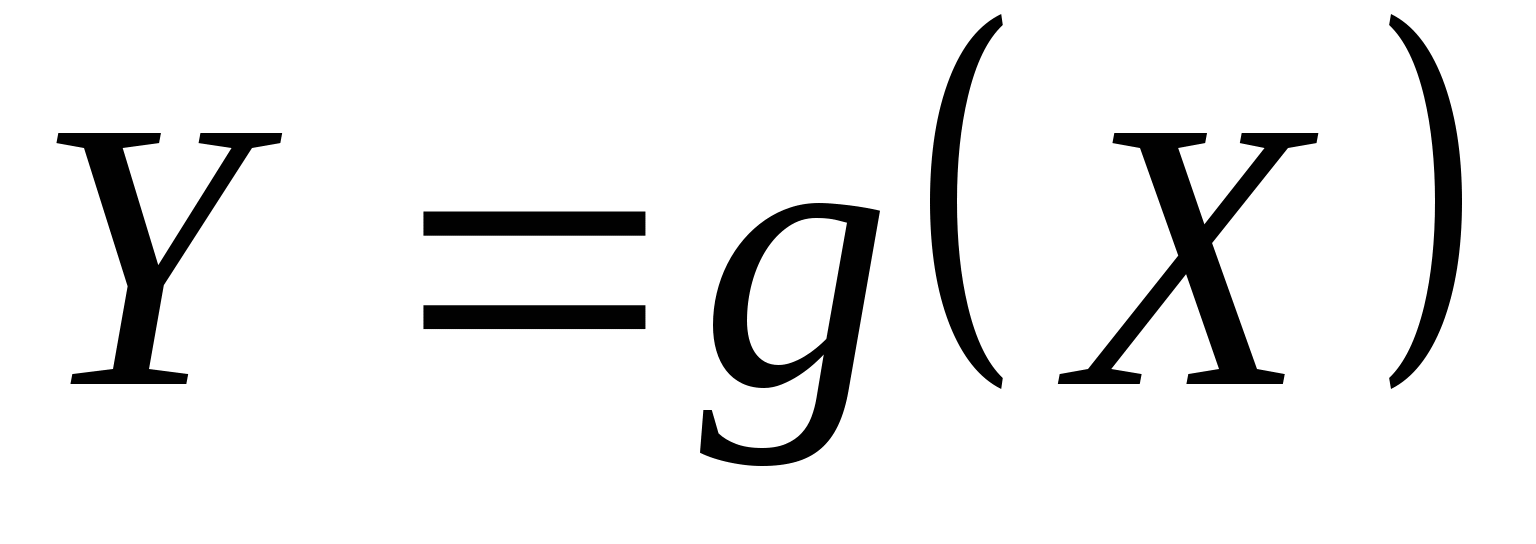 的分布. 的分布. 一、离散型随机变量函数的分布 设 是离散型随机变量,则 是离散型随机变量,则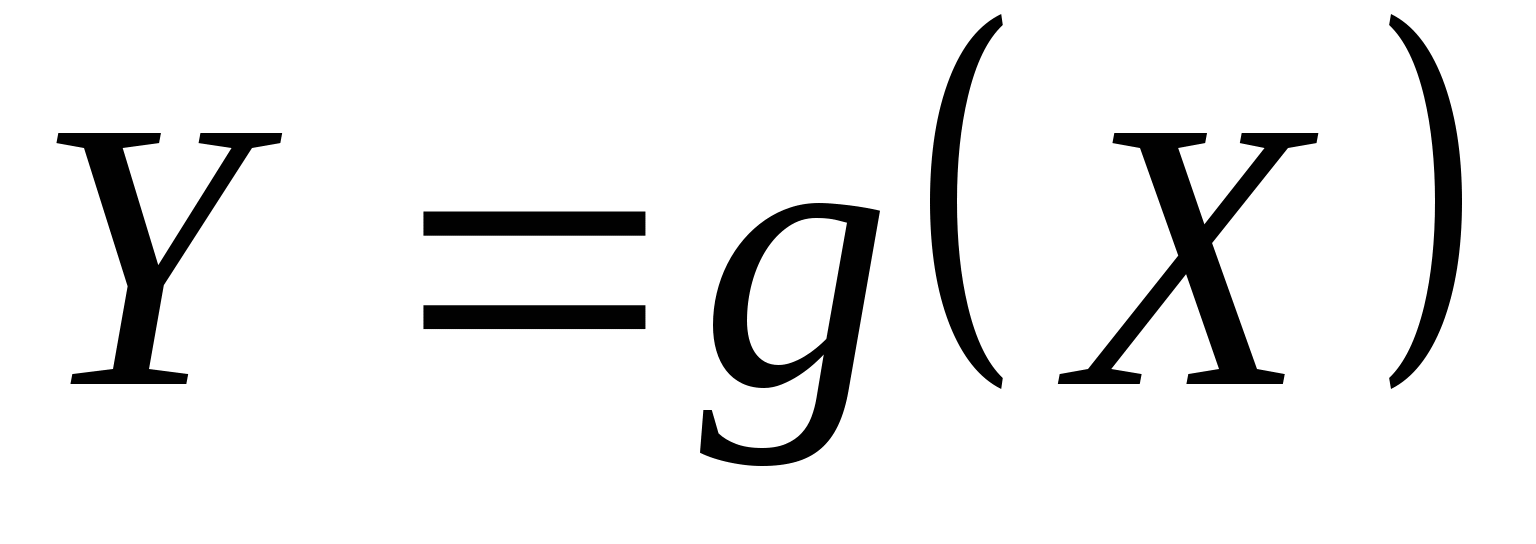 也是离散型随机变量,由 也是离散型随机变量,由 的分布律如何求 的分布律如何求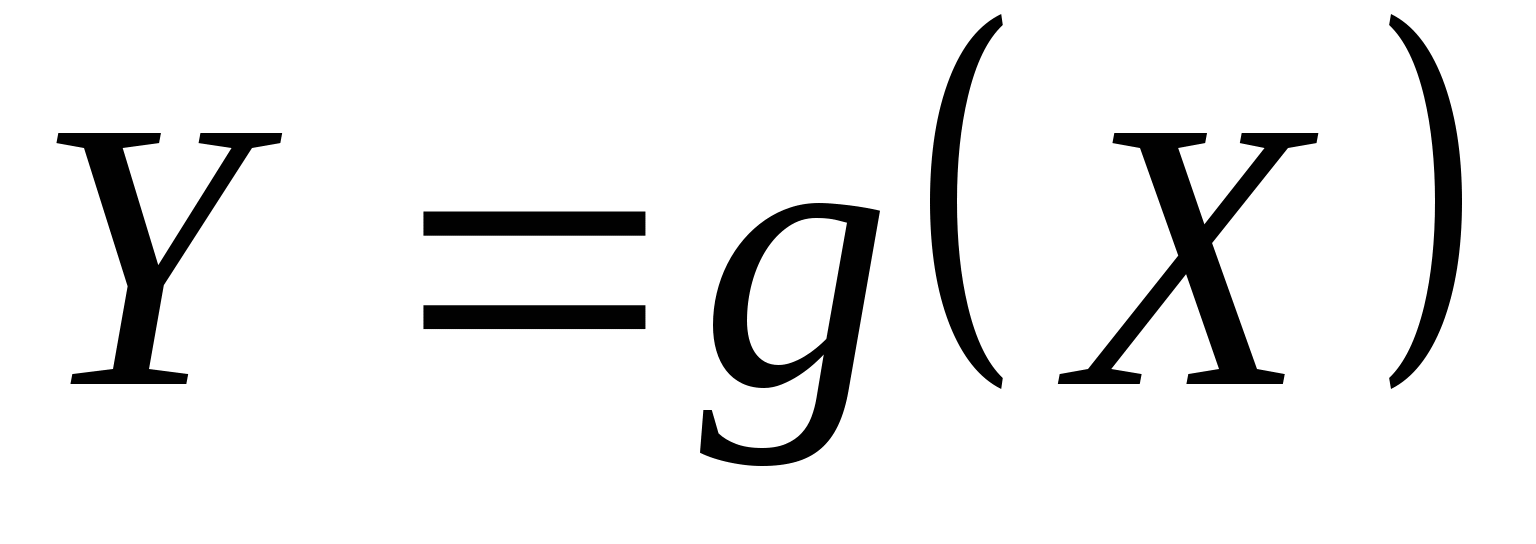 的分布律.先看下面的例子. 的分布律.先看下面的例子. 例 设离散型随机变量 设离散型随机变量 的分布律为 的分布律为  -1 0 1 2 -1 0 1 2
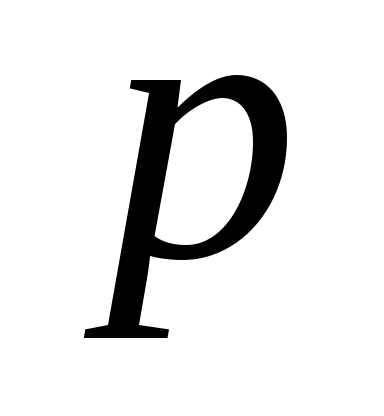  0.1 0.3 0.2 0.4 0.1 0.3 0.2 0.4
求(1)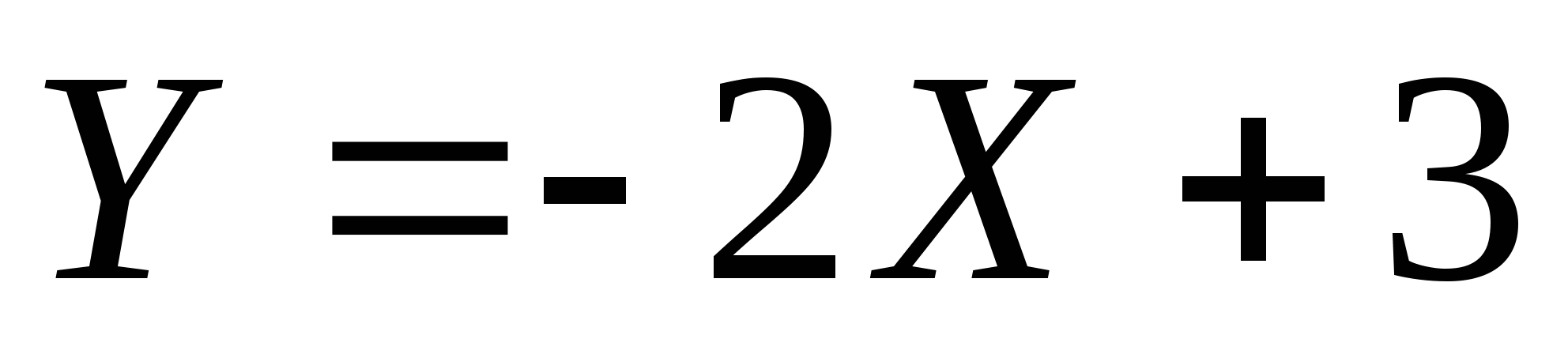 的分布律;(2) 的分布律;(2)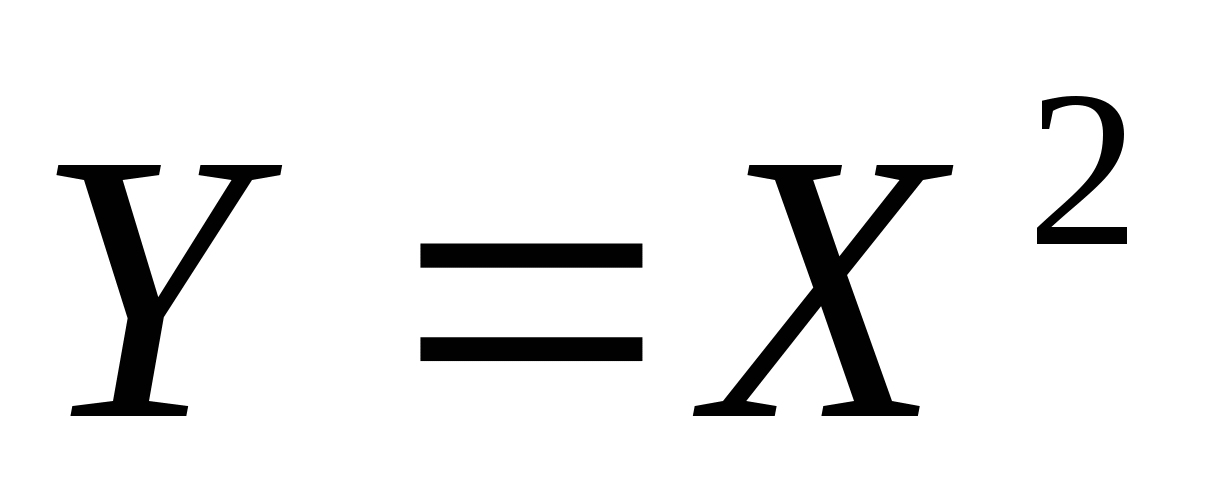 的分布律. 的分布律. 二、连续型随机变量函数的分布 设 为连续型随机变量,且其密度函数为 为连续型随机变量,且其密度函数为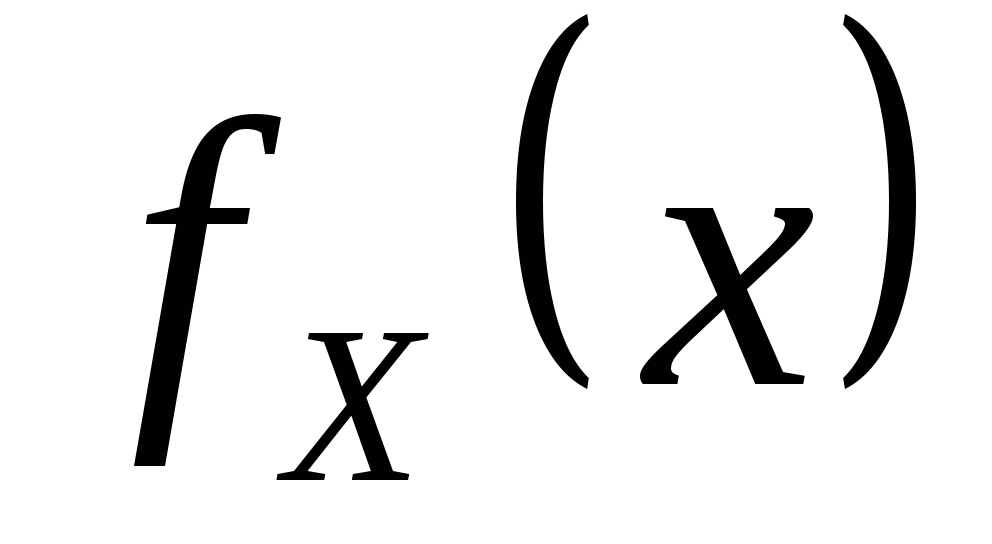 , ,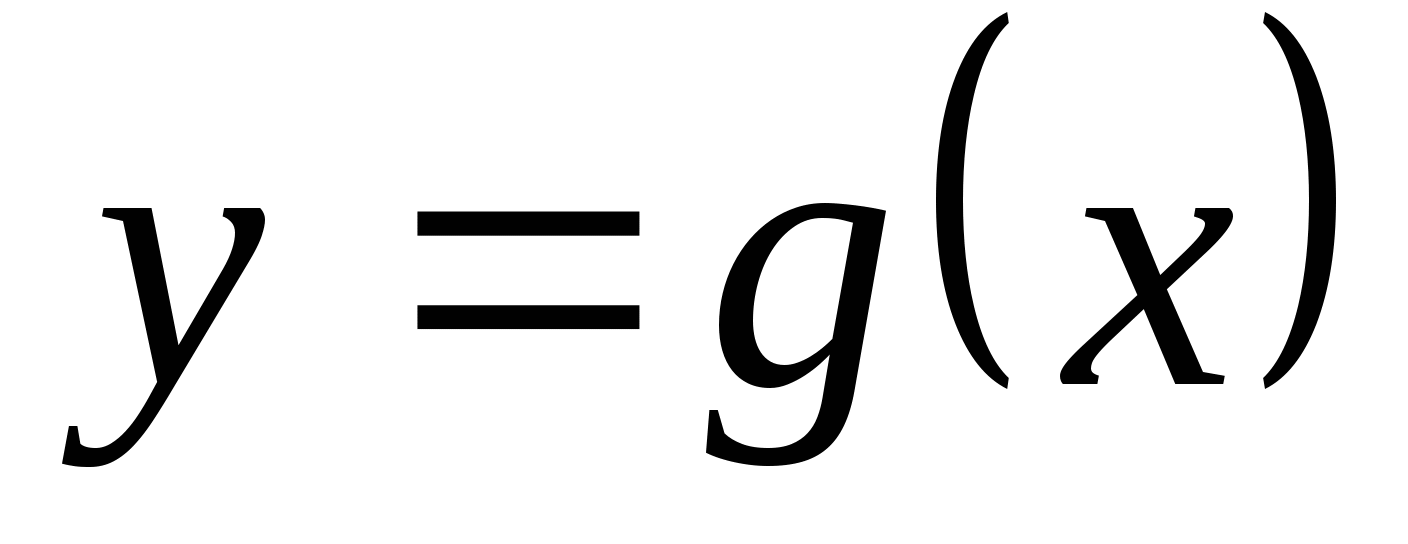 为连续函数,则 为连续函数,则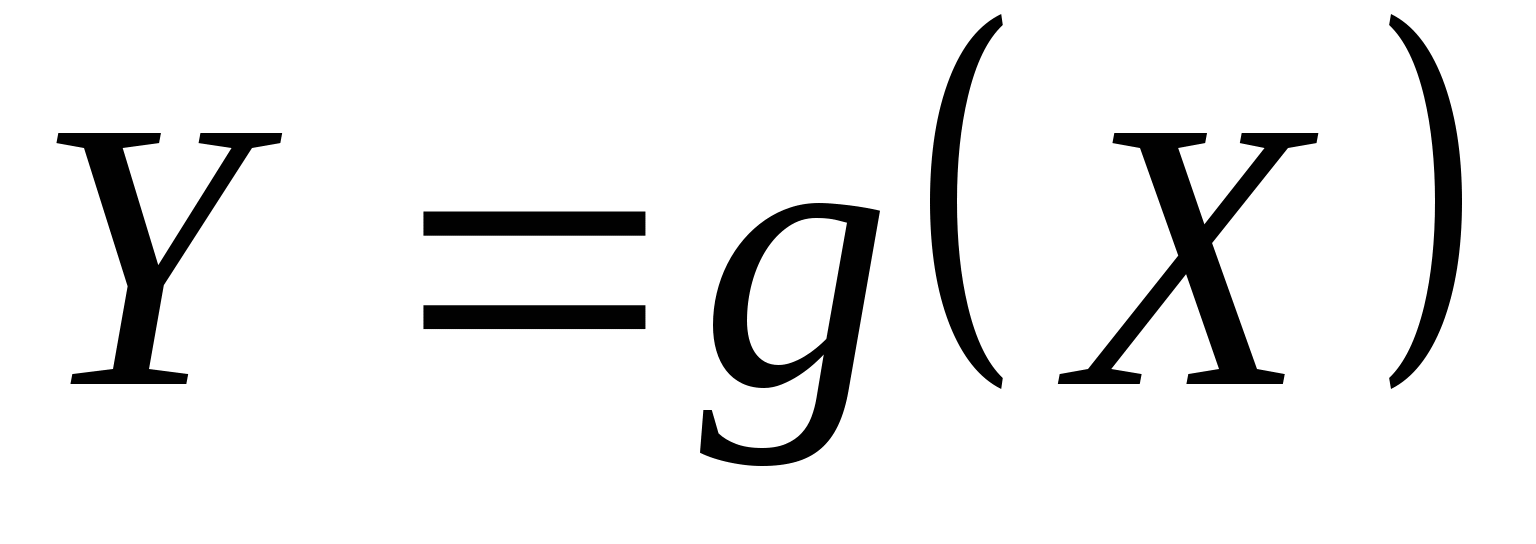 也是连续随机变量.其分布函数为 也是连续随机变量.其分布函数为 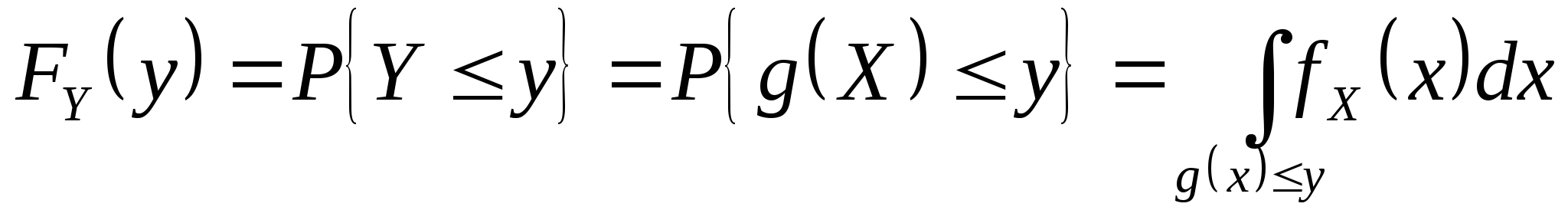
则Y的密度函数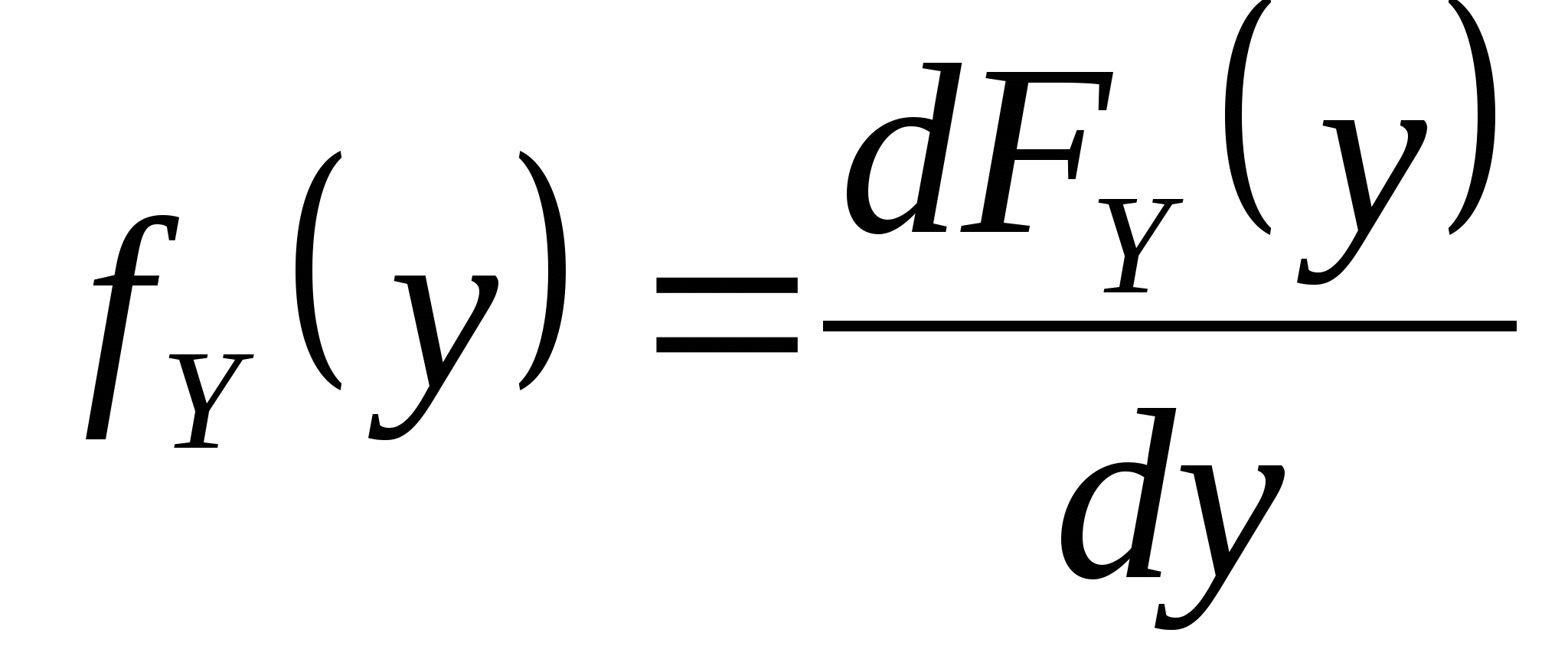 . . 例 设 的密度函数为 的密度函数为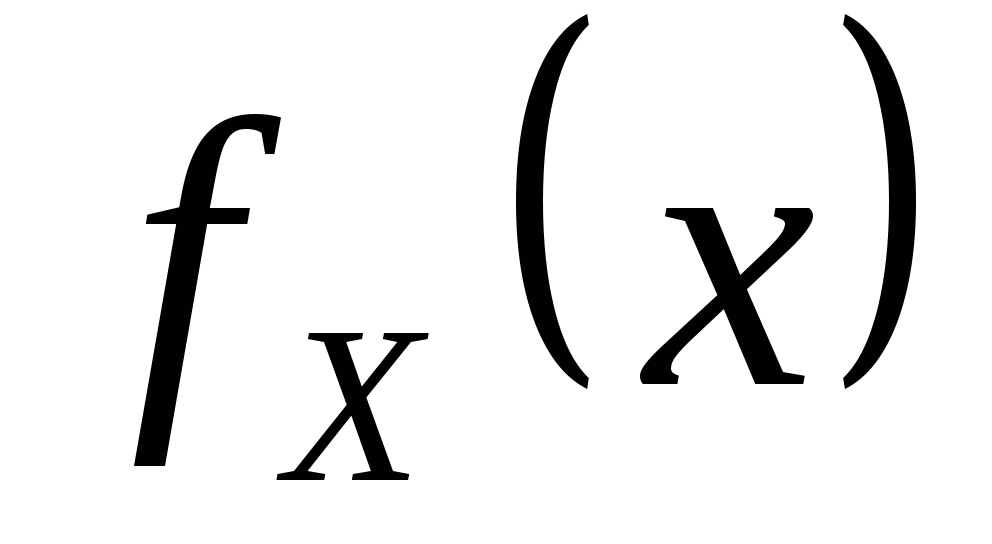 ,求 ,求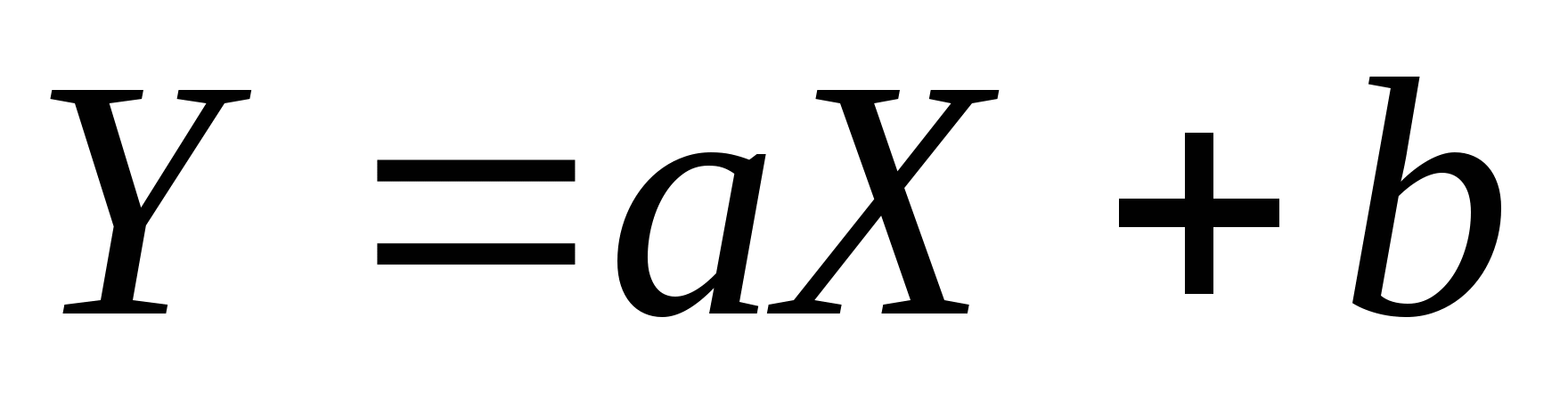 ( (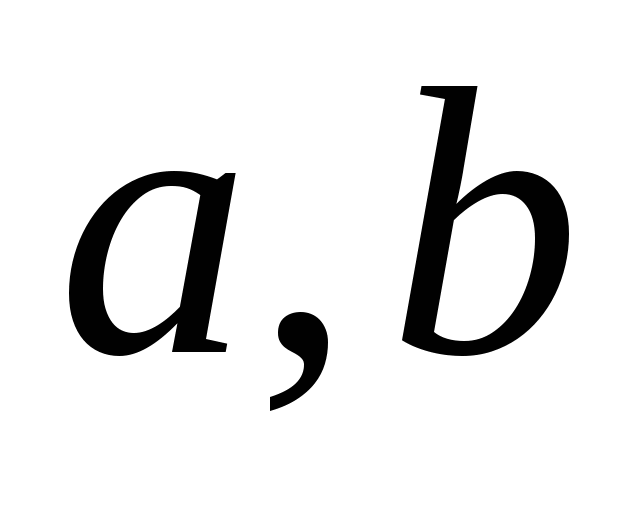 都是常数,且 都是常数,且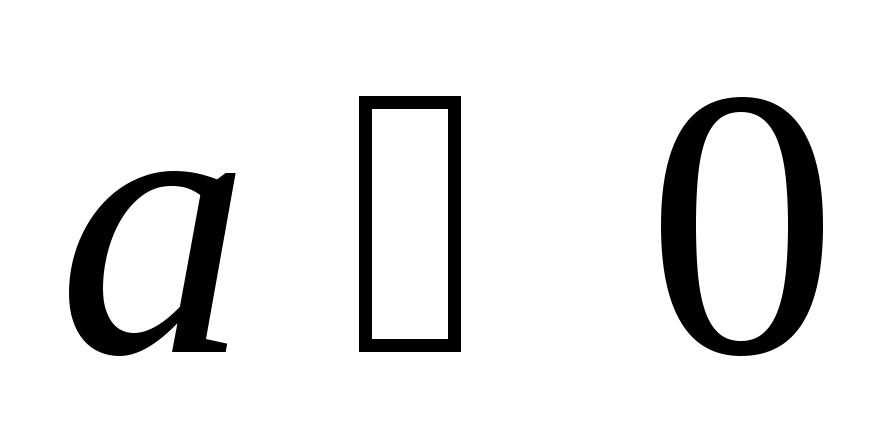 )的密度函数. )的密度函数. 例 设 在区间(0,2)内服从均匀分布,求 在区间(0,2)内服从均匀分布,求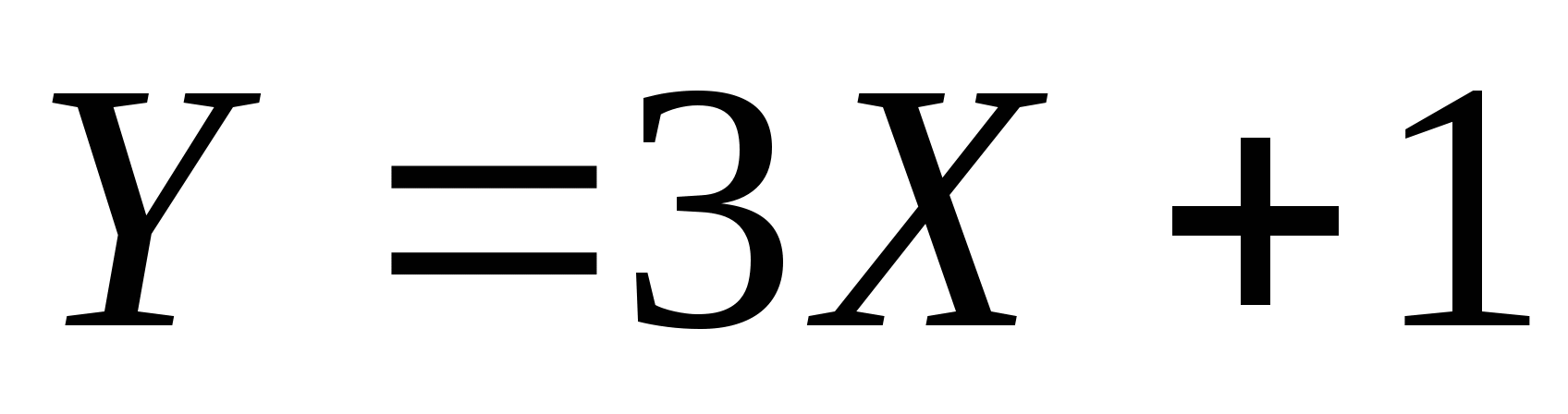 的分布密度. 的分布密度. 小结:这一讲我们介绍了随机变量函数的分布. 对于连续型随机变量,在求Y=g(X) 的分布时,关键的一步是把事件 { g(X)≤ y } 转化为X在一定范围内取值的形式,从而可以利用 X的分布来求 P { g(X)≤ y }. 第四章 随机变量的数字特 教学基本要求: 理解数学期望和方差的概念 掌握离散型随机变量数学期望和方差的计算,掌握数学期望和方差的性质 会计算连续型随机变量的数学期望。
重点: 1、数学期望和方差的性质及计算。 难点: 1、方差的计算。 第一节 数 学 期 望 一、数学期望的定义 定义1 设 是离散型随机变量,其分布律为: 是离散型随机变量,其分布律为:  ( ( ), ),
若无穷级数 时,数值 时,数值 叫做随机变量 叫做随机变量 的数学期望或均值,简称为期望,记作 的数学期望或均值,简称为期望,记作 ,即 ,即 (1) (1) 否则,称 的数学期望不存在. 的数学期望不存在. 例 设 的分律为 的分律为
求 例 设随机变量 服从( 服从( )分布,求 )分布,求  定义2 设 是连续型随机变量,其概率密度为 是连续型随机变量,其概率密度为 ,若 ,若 ,积分 ,积分 叫做随机变量 叫做随机变量 的数学期望,记作 的数学期望,记作 ,即 ,即 
否则,称随机变量 的数学期望不存在. 的数学期望不存在. 例 4 已知连续型随机变量 的概率密度为 的概率密度为 
求 的数学期望. 的数学期望. 例5 设 ,求 ,求 . . 类似对 可求得 可求得  . . 二、数学期望的性质 性质1 设 是常数,则 是常数,则 . . 性质2 设 是常数,则 是常数,则 . . 性质3  . . 性质4 设随机变量 和 和 相互独立,则有 相互独立,则有 . . 例7 设 ,求 ,求 . . 三、随机变量函数的数学期望 定理1 设 是一维随机变量, 是一维随机变量, . . (1)若 为离散型随机变量,其分布律为 为离散型随机变量,其分布律为  ( ( ) )
 ,则 ,则 的数学期望为 的数学期望为
 ; ;
(2)若 为连续型随机变量,其概率密度为 为连续型随机变量,其概率密度为 , , ,则 ,则 的数学期望为 的数学期望为  . .
例8 设随机变量 的分布律为 的分布律为
求 . . 第二节 方 差 一、方差的概念 定义1 设 是一个随机变量,如果 是一个随机变量,如果 存在,则将其叫做 存在,则将其叫做 的方差,记作 的方差,记作 ,即 ,即  . .
根据此定义,当 是离散型随机变量时,其分布律为 是离散型随机变量时,其分布律为  ,( ,( ) )
即得  . . 当 是连续型随机变量时,其概率密度为 是连续型随机变量时,其概率密度为 ,即得 ,即得  . .
对任意随机变量 ,若 ,若 都存在,则有 都存在,则有  . .
例1 设离散型随机变量X的分布律为

求X的方差. 例 2 已知连续型随机变量 的概率密度为 的概率密度为  , ,
二、方差的性质 设 是一个常数,随机变量 是一个常数,随机变量 和 和 的方差 的方差 和 和 都存在.根据方差的定义及数学期望的性质,容易证明随机变量的方差具有如下的性质. 都存在.根据方差的定义及数学期望的性质,容易证明随机变量的方差具有如下的性质. 性质1  . 性质2 . 性质2  . 性质3 . 性质3  性质4 若随机变量 和 和 相互独立,则 相互独立,则 . . 证明略. 三、几个常见随机变量的方差 例 设随机变量 服从( 服从( )分布,其分布律为 )分布,其分布律为  , , ( ( ), ),
求 . .
例 若随机变量 服从二项分布: 服从二项分布: ,求 ,求 . . 例 设随机变量 服从均匀分布 服从均匀分布 ,求 ,求 . . 例 设随机变量 ,求 ,求 . . 当 ,令 ,令 ,则 ,则 .于是有 .于是有 
| 


